
この記事では主にヒープソートのJS実装を紹介します。これを必要とする友人に参考にしてもらいます
完全な二分木: 二分木では、最後の層を除いて、他の層のノード数が最大に達し、最後の層のすべてのノードが左側に集中します(ノードが欠落する可能性があります)。右側のノードは左側のノードがいっぱいの場合のみ)。
ビッグトップヒープ: ルートノードが最大値であり、各ノードの値はその子ノードの値以上です。
スモールトップヒープ: ルートノードが最小値であり、各ノードの値はその子ノードの値以下です。
ヒープストレージ: ヒープは配列によって実装され、これはバイナリツリーのレベル順の走査に相当します。以下に示すように:

i+1 および 2 i+2 です。
i+2 です。
ヒープソートアルゴリズム
次に、上記のバイナリツリーを昇順にソートする必要があります。これは 3 つのステップに分かれています: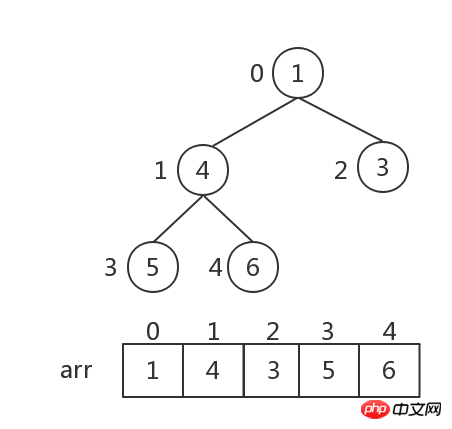
ここで、初期バイナリツリーを大きな上部ヒープ (heapify) に変換します。ルートノードが最大値になった時点で、最後のノードと入れ替えます。
最後のノードを除いて、残りのノードで構成される新しいヒープを大きな最上位ヒープに変換します。このとき、ルートノードは最大値以下であり、最後のノードと交換されます。
ヒープ内の要素の数が 1 (または、それに対応する配列の長さが 1) になるまでステップ 2 を繰り返し、並べ替えが完了します。
このプロセスの詳細を以下に示します:
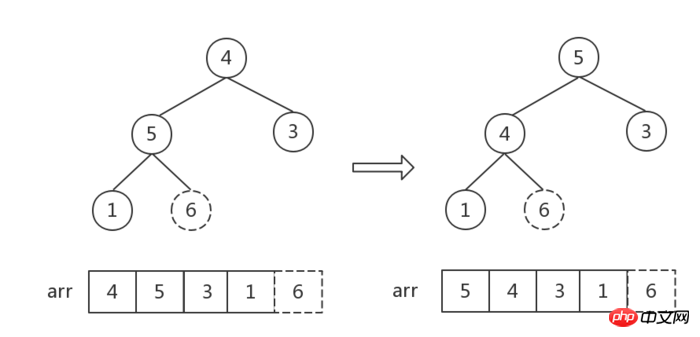
大きな上部ヒープを初期化し、最初に最後の非リーフ ノードを選択します (親ノードと子ノードのサイズ関係を調整するだけで済みます) 、葉ノード間のサイズ関係を調整する必要はありません)。配列が arr であると仮定すると、最初の非リーフ ノードの添字は次のようになります: i = Math.floor(arr.length/2 - 1) = 1。図の点線のボックスに示すように、これは数値 4 です。 , 3つの数字を見つける 最大値は親ノードと交換されます。
その後、添字 i が 1 減分されます (つまり、最初の非リーフ ノードから開始して、すべての非リーフ ノードを右から左、下から上にたどります)。後続の調整はすべて同じです。親ノードと子ノードの間で最大値を見つけて交換します。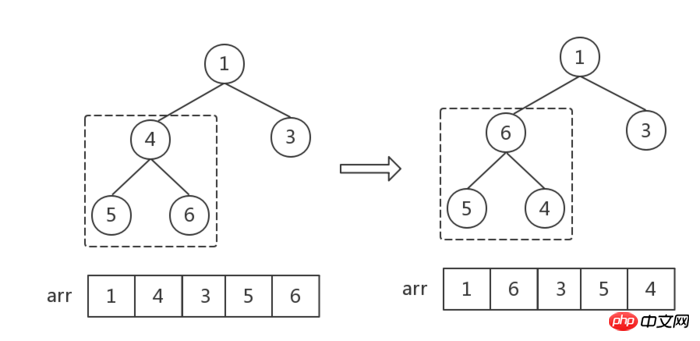
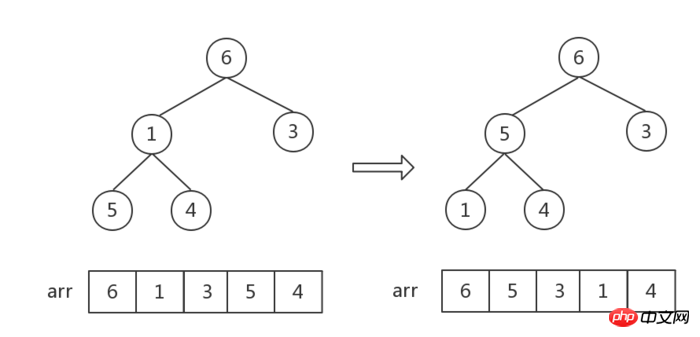
 ステップ 2:
ステップ 2:
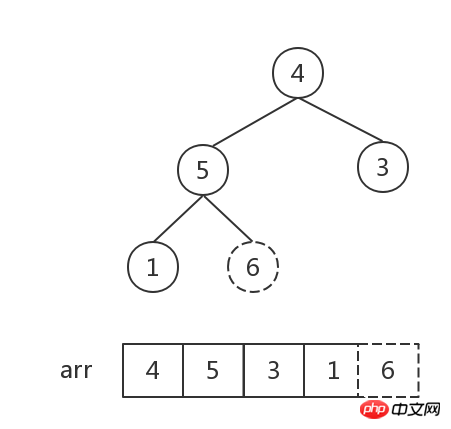
現在の最後のノード 6 (つまり、最大値) を除いて、残りのノード [4,5,3,1] の新しいヒープを形成し、それを大きな上部ヒープに変換します (今回は、ルートノード以外の他のノードはすべて大きなトップヒープの特性を満たしているため、ルートノード4から調整を開始できます。つまり、4があるべき位置を見つけます。
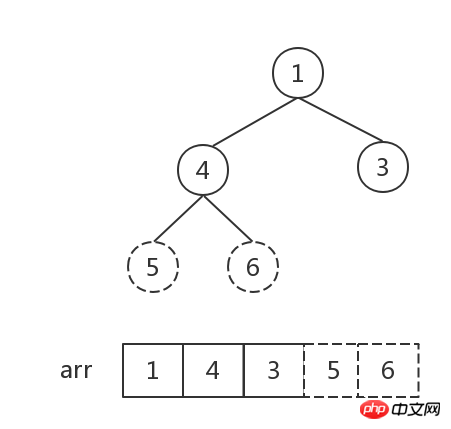 次に、ヒープ内の要素の数が 1 になるまでステップ 2 を繰り返します。ヒープ内の要素の数は 1 で、ソートが完了しました。
次に、ヒープ内の要素の数が 1 になるまでステップ 2 を繰り返します。ヒープ内の要素の数は 1 で、ソートが完了しました。
// 交换两个节点
function swap(A, i, j) {
let temp = A[i];
A[i] = A[j];
A[j] = temp;
}
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设 结点 i 以下的子堆已经是一个大顶堆,adjustheap 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 adjustheap 操作,所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function adjustHeap(A, i, length) {
let temp = A[i]; // 当前父节点
// j<length function>=0; i--) {
adjustHeap(A, i, A.length);
}
// 排序,每一次for循环找出一个当前最大值,数组长度减一
for(let i = Math.floor(A.length-1); i>0; i--) {
swap(A, 0, i); // 根节点与最后一个节点交换
adjustHeap(A, 0, i); // 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
}
}
let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);</length>プログラムのメモ: ノード i の下のヒープを大きなトップ ヒープに編成することは、実際には、ノード i の下のサブヒープがすでに大きなトップ ヒープであると仮定して、adjustHeap 関数を実装することに注意してください。実際の機能は、ノード i を含むヒープ内のノード i の正しい位置を見つけることです。後で最初のヒープを実行するとき、for ループが heapSort に書き込まれます。最初の非リーフ ノードから開始して、adjustHeap 操作が各非リーフ ノードで実行されるため、各AdjustHeap ノードのサブi の下のヒープはすでに大きな上部ヒープです。
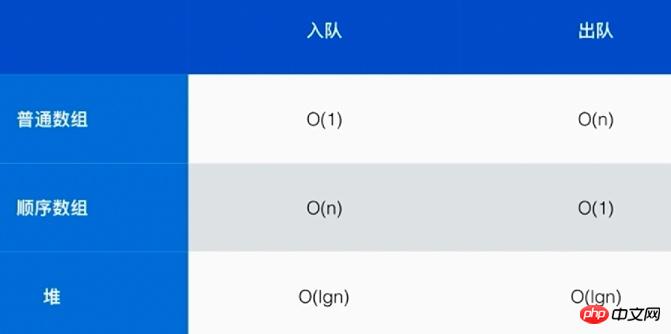
複雑さの分析:AdjustHeap 関数は、ヒープのレイヤーごとに 1 つのノードのみをトラバースします。これは、n 個のノードを持つ完全なバイナリ ツリーの深さは [log2n]+1 であるため、adjustHeap の複雑さは O(logn ) であり、外側のノードはループの合計は f(n) 回であるため、最終的な複雑さは O(nlogn) になります。
以上がJSはヒープソートを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。