この記事は、css3 マトリックスの詳細な使用法に関する関連情報を主に紹介しています。編集者が非常に優れていると考えたので、参考として共有します。エディターに従って
css3 行列の変更を確認してみましょう。アプリケーションの形式は
transform: matrix(a,b,c,d,e,f);
で、これは
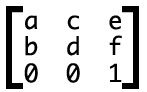
に対応します。実際のアプリケーションでの変換は次のとおりです:
。
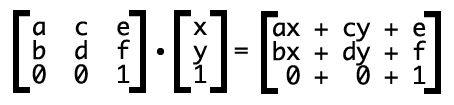
ax+cy+e = 横座標 bx+dy+f = 縦座標 なぜ余分な 0 0 1 があるのでしょうか? なぜなら、パラメータを構成するためのtranslate 行列
の基本形式は次のとおりです:transform: matrix(1, 0, 0, 1, X, Y); // X 横向平移, Y 纵向平移
scale 行列
scale (スケール) 行列も非常に単純です。// 将 X 轴缩放 A 倍 // 将 Y 轴缩放 B 倍 matrix(A, 0, 0, B, 0,0);
// 得到: X 轴 = 0.3*x + 100 // 得到: Y 轴 = 0.2*x + 200 matrix(0.3,0,0,0.2,100,200);
rotate 行列
rotateは実際には多くのことを行う必要があります。三角関数を使用して、まず回転角度を決定します (時計回りに回転します)。次に、sinθ と cosθ を計算します。これも三角関数ですが、tanθ が使用されます。形式は次のとおりです:matrix(cosθ,sinθ,-sinθ,cosθ,0,0) // 就是 cs-sc
3D 変換行列
3D 変換は 4*4 行列ですが、Z が 1 つ多い点が異なります。 。 // これはスケーリングされた 3D マトリックスです対応する CSS は次のように記述されます:
// 将 Y 轴向 X 轴倾斜 A° // 将 X 轴向 Y 轴倾斜 B° matrix(1,tan(A),tan(B),1,0,0)
以上がこの記事の全内容です。その他の関連事項については、皆様の学習に役立つことを願っています。コンテンツについては、PHP 中国語ネットにご注目ください。
関連する推奨事項: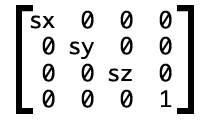
HTML と CSS で三角形のアイコンを描画する方法について
CSS3 について remの分析（フォントサイズの設定）
以上がcss3でのマトリックスの使い方についての詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
