
今回は、フロントエンドでのソートアルゴリズムの例について詳しく説明します。フロントエンドでソートアルゴリズムを使用する場合の注意事項は何ですか?実際のケースを見てみましょう。 。
一昨日、Ruan Yifeng 先生のクイックソートアルゴリズムについて苦情を言っている Zhihu の記事を見ました。ここで余談を付け加えておきたいと思います。本は信じたほうが良いです。学習のプロセスは、常に間違いを発見し、修正するプロセスです。誰かがこの間違いを修正するのを手伝ってくれたら、私たちは喜ぶべきですが、私はルアン・イーフェン先生を批判するべきではないと思います。常に学び、間違いを修正し、成長するので、誤解を招くことは問題ではありません。では、JavaScript の作者はどこにいるのでしょうか?誰もが間違いを犯すでしょう、私たちももっと考え、それを懐疑的な態度で受け入れ、これが最善の解決策であるかどうかを常に考える必要があります。そして、これが私たちがすべきことだと思います。プロのフロントエンドである私は、アイデアのさまざまなソートアルゴリズムをうまく実装できません。とても恥ずかしいので、時間をかけてC言語説明+中国語版を読みました。 .pdf>>. 以下に、私が理解しているさまざまなアイデアのソート アルゴリズムをまとめます。何か間違っている点があれば、ご指摘ください。みんなが一緒に学んで進歩することが一番幸せなことだと思います~
1. 知っておくべき関連概念1.1 時間計算量(1) 時間計算量の概念アルゴリズムの複雑度は、アルゴリズムの実行時間を定性的に表します。この関数の低次項と高次項の係数を除いた、ビッグオー表記が一般的に使用されます。
for(i = 1; i <p style="text-align: left;"> T(n) = n^3 + n^2 を取得でき、n^3 が T(n) と同じ桁であると判断でき、f(n)=n ^3; の場合、 T(n) / f(n ) = 1 + 1/n 制限は定数 1 であるため、このアルゴリズムの時間計算量は次のようになります:</p> T(n) = O(n^3);<p style="text-align: left;"><br></p>説明: 便宜上、配列要素の代数的な数を N とします。<p style="text-align: left;"><strong></strong>2. ソートアルゴリズム</p><h1 style="text-align: left;">2.1 </h1>バブルソート<h2 style="text-align: left;">
<a href="//m.sbmmt.com/code/12106.html" target="_blank"></a>2.1.1 主なアイデア:</h2><h3 style="text-align: left;">バブルソートの主なアイデアは次のとおりです。長さ n の配列を走査します。i は n-1 から 1 であり、配列の最初の i 要素の最大値が i の位置に配置されます。バブル ソートが垂直の水柱であると想像してください。大きな値(重い値)は沈み続け、小さな値(軽い値)は浮き上がり続けるため、トラバースが完了すると、各位置の値は前の値よりも大きくなります。並べ替えが完了しました。</h3><p style="text-align: left;">2.1.2 時間計算量</p><h3 style="text-align: left;">最悪の場合の時間計算量: o(n^2);</h3>最良の場合の時間計算量: o(n^2);<p style="text-align: left;"><br>2.1.3 の図ソートプロセス:</p><h3 style="text-align: left;"></h3> 図のループ出口は、内側のループを抜けることです<p style="text-align: left;"> <strong></strong><br></p><h3 style="text-align: left;">2.1.4 代码实现:</h3><h4 style="text-align: left;">冒泡排序-非递归实现</h4><pre class="brush:php;toolbar:false">function bubbleSort(arr) {
for(var i = arr.length - 1; i > 1; i--) {
for(var j=0; j arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr); // [8, 21, 32, 34, 51, 64]function bubbleSort(arr, n) {
if(n arr[j+1]) {
var temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
return bubbleSort(arr, --n);
}
}
var arr = [34,8,64,51,32,21];
bubbleSort(arr, arr.length); // [8, 21, 32, 34, 51, 64]插入排序有 n-1 趟排序组成,对于 i=1 到 i=n-1 趟,内层循环j从 i 到 1, 如果这其中有 j-1 位置上的元素大于 i 位置上的元素,就将该元素后移,知道条件不成立退出循环,这个时候大的值都被移动到后面了,j这个位置就是i位置上的元素应该在的位置.这样保证了每次循环i位置前的所有元素都是排好序的,新的循环就只需要 将 i 位置上的元素 和 j-1(也就是初始的 i-1) 位置上的元素作比较,如果大于则无需再往前比较,如果小于则继续往前比较后移.
最坏情况下的时间复杂度: o(n^2);
最好情况下的时间复杂度: o(n);
图解中的出循环是退出内层循环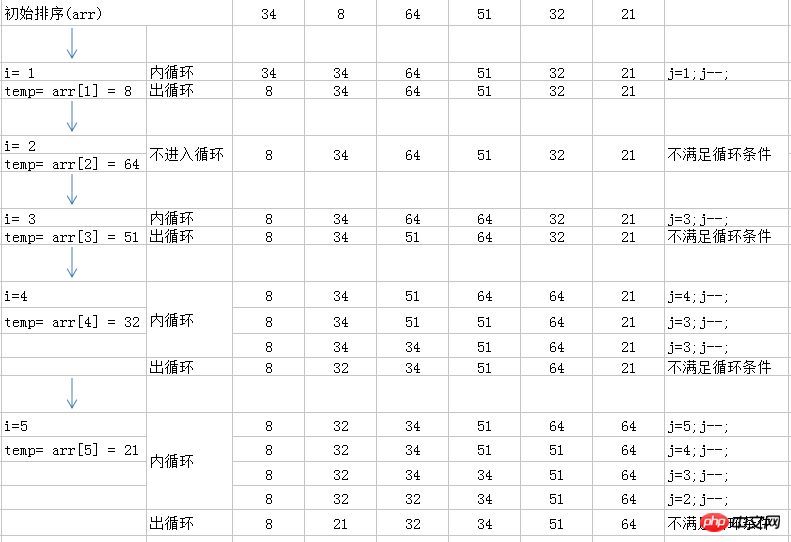
function insertSort(arr) {
var n = arr.length,temp = 0;
for(var i = 1; i 0 && arr[j-1] > temp; j--) {
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr); // [8, 21, 32, 34, 51, 64]function insertSort(arr, n) {
if(n > 0 && n 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
j--;
}
arr[j] = temp;
i++;
return insertSort(arr, i);
}
return arr;
}
var arr = [34,8,64,51,32,21];
insertSort(arr, 1); // [8, 21, 32, 34, 51, 64]; // 这个函数的调用限定了第一次调用n的值只能传1顾名思义,快速排序是在实践中最快的已知排序算法,它的平均运行时间是O(Nlog₂N).快速排序的关键在于枢纽元的选取,有一种比较推荐的选取方法就是选取左端的值,右端的值,中间位置的值(L(left + right) / 2)这三个数的中位数.举例: 输入为8,1,4,9,6,3,5,2,7,0, 左边元素8, 右边元素0,中间位置上的元素L(0+9)/2是4位置上的元素是6,L在表示向下取整.
8,0,6的中位数,先排序0,6,8, 这三个数的中位数是6.
通过一趟排序将要排序的部分分割成独立的两部分,其中一部分数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据进行快速排序,整个排序过程可以递归进行,依次达到整个数据变成有序序列.
第一步: 设置两个变量i,j,排序开始的时候: i=left,j=right-1,left和right分别表示要进行快速排序序列的起始索引和结束索引;
第二步: 从数组中随机选取一个元素,将其与arr[left]进行交换,即privot = arr[left],保证每一次的基准值都在序列的最左边;
第三步: 由j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于privot 的值arr[j],将arr[i]与arr[j]互换;
第四步: 从i开始向后搜索,即由前开始向后搜索(i++),找到一个大于privot 的arr[i],将arr[i]与arr[j]互换;
第五步: 重复第三步和第四步,直到不满足i
平均情况下的时间复杂度: o(nlog₂n);
最好情况下的时间复杂度: o(n);

function quickSort(arr, left, right) {
if(left >= right) return;
var i = left;
var j = right - 1;
var privot = arr[left];
//console.log(privot);
while(i = privot) j--;
arr[i] = arr[j];
while(i<j var quicksort><h4 style="text-align: left;">快速排序-非递归实现</h4>
<pre class="brush:php;toolbar:false">function mainProduce(arr, left, right) {
var i = left, j = right - 1;
var rendomIndex = Math.floor(Math.random() * (j - i)) + left;
var temp = arr[left];arr[left] = arr[rendomIndex];arr[rendomIndex] = temp;
var privot = arr[left];
while(i = privot) j--;
var temp = arr[i];arr[i] = arr[j];arr[j] = temp;
while(i<j> left + 1) {
s.push(left);s.push(mid);
}
if(mid left + 1) {
s.push(left);s.push(mid);
}
if(mid <h2 style="text-align: left;">2.4 希尔排序</h2>
<h3 style="text-align: left;">2.4.1 主要思想</h3>
<p style="text-align: left;">希尔排序是把记录按照下标的一定增量分组,对每组使用插入排序;随着增量逐渐减少,分割的数组越来越大,当增量减至1,整个<a href="//m.sbmmt.com/code/54.html" target="_blank">数组排序</a>完成,算法终止.</p>
<h3 style="text-align: left;">2.4.2主要步骤</h3>
<p style="text-align: left;">第一步: 选取一个增量d,初始值是Math.floor(len/2);<br>第二步: 然后将数组中间隔为增量d的组成新的分组,然后对这个分组的元素排序,完成排序后,增量除以2得到新的增量;<br>第三步: 重复第二步,直到增量为1,间隔为1的元素组成的分组就是整个数组,然后再对整个数组进行插入排序,得到最后排序后数组.</p>
<p style="text-align: left;">希尔排序是不稳定的,它在不断地交换的过程中会改变原来相等的元素的顺序.</p>
<h3 style="text-align: left;">2.4.3 时间复杂度</h3>
<p style="text-align: left;">平均情况下的时间复杂度: o(nlog₂n);<br>最好情况下的时间复杂度: o(n);</p>
<h3 style="text-align: left;">2.4.4 フロントエンドのソートアルゴリズム例の詳細説明</h3>
<p style="text-align: left;"><img src="https://img.php.cn/upload/article/000/061/021/2f13ca0ab50333d1dad5851595e7225d-3.jpg" alt="フロントエンドのソートアルゴリズム例の詳細説明" title="フロントエンドのソートアルゴリズム例の詳細説明"></p>
<p style="text-align: left;">图片源于自百度百科: 图片来源</p>
<h3 style="text-align: left;">2.4.5 代码实现:</h3>
<h4 style="text-align: left;">希尔排序-递归实现</h4>
<pre class="brush:php;toolbar:false">function shellSort(arr, increment) {
var len = arr.length;
if(increment > 0) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
return shellSort(arr, Math.floor(increment/2));
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr, Math.floor(arr.length / 2));function shellSort(arr) {
var len = arr.length;
for(var increment = Math.floor(len / 2); increment > 0; increment = Math.floor(increment / 2)) {
for(var i = increment; i = 0 && arr[j] > arr[j + increment]; j -= increment) {
var temp = arr[j];
arr[j] = arr[j + increment];
arr[j + increment] = temp;
}
}
}
return arr;
}
var arr = [49,38,65,97,76,13,27,49,55,04];
shellSort(arr);第一步: 将一个数组以中间值截取为为两个数组,分别将其排好序;
第二步: 申请一个空间,使其大小为两个已经排序的序列之和,该空间用来存放合并后的序列;
第三步: 设定两个指针,分别指向两个已排序序列的起始位置;
第四步: 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置.
重复第四步直到有一个某一指针超出序列尾;
将另一序列的所有元素复制到合并序列尾.
归并排序是稳定的,它在不会改变原来相等的元素的顺序.
平均情况下的时间复杂度: O(nlog₂n);
最好情况下的时间复杂度: O(nlog₂n) ;

var result = [];
function mergeArray(left, right) {
result = [];
while(left.length > 0 && right.length > 0) {
if(left[0] <p>相信看了本文案例你已经掌握了方法,更多精彩请关注php中文网其它相关文章!</p><p>推荐阅读:</p><p><a href="//m.sbmmt.com/js-tutorial-398003.html" target="_blank">React结合TypeScript和Mobx步骤详解</a><br></p><p><a href="//m.sbmmt.com/js-tutorial-398045.html" target="_blank">react实现选中li高亮步骤详解</a><br></p>以上がフロントエンドのソートアルゴリズム例の詳細説明の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。