
この記事は 3 つのパートに分かれています
1. JS デジタル精度損失の典型的な問題
1. 2 つの単純な浮動小数点数を加算します
0.1 + 0.2 != 0.3 // true

これは実際には Firebug の問題ではありません。アラートを使用してみてください (笑、冗談です)。
Java 操作の結果を見てください
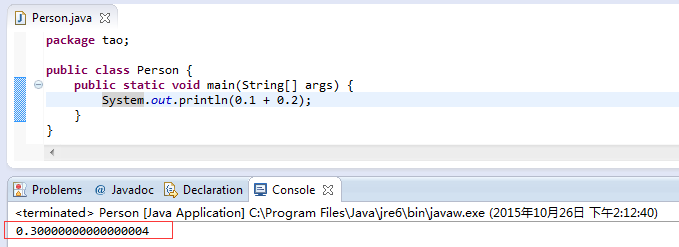
もう一度 Python を見てみましょう

2. 大整数演算
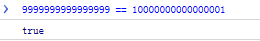
16 桁と 17 桁の数字が等しいというのは意味がありません。
別の例
var x = 9007199254740992 x + 1 == x // ?
結果を見る

3 つの見解が再び覆されました。
3. toFixed は (Chrome)
を丸めません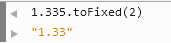
オンラインで Chrome の価格が他のブラウザと一致しないケースがありました
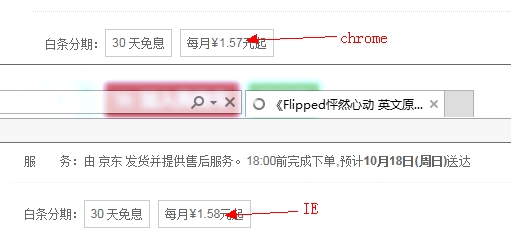
2. JS 数値の精度が失われる理由
コンピューターのバイナリ実装とビット制限により、有限に表現できない一部の数値が制限されます。 pi 3.1415926...、1.3333... など、一部の無理数を有限に表現できないのと同じです。 JS は IEEE 754 仕様に従い、倍精度ストレージを使用し、64 ビットを占有します。写真の通り
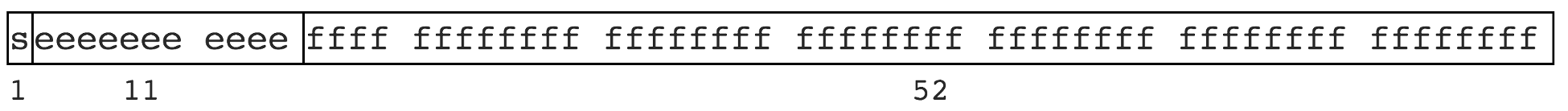
意味
浮動小数点数 (
など)0.1 >> 0.0001 1001 1001 1001…(1001无限循环) 0.2 >> 0.0011 0011 0011 0011…(0011无限循环)
現時点では四捨五入は10進数の真似しかできませんが、2進数は0と1の2つの数値しかないので四捨五入すると0と1になります。これが、コンピュータの一部の浮動小数点数演算におけるエラーや精度の低下の根本原因です。
大きな整数の精度の低下は、浮動小数点数の精度の低下と本質的に同じです。仮数の最大桁数は 52 です。したがって、JS で正確に表現できる最大の整数は Math.pow(2, 53) です。 、10 進数では 9007199254740992 です。
9007199254740992 より大きいものは精度が失われる可能性があります
9007199254740992 >> 10000000000000...000 // 共计 53 个 0 9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0 9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0
実は
9007199254740992 + 1 // 丢失 9007199254740992 + 2 // 未丢失 9007199254740992 + 3 // 丢失 9007199254740992 + 4 // 未丢失
結果は写真の通りです
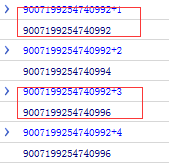
上記のことから、コンピューターのバイナリ表現では、一見有限に見える数値が無限であることがわかります。格納桁数の制限により、「丸め」が発生し、精度が失われます。
3. 解決策
整数の場合、演算結果が Math.pow(2, 53) を超えない限り、フロントエンドで問題が発生する可能性は比較的低いと考えられます。精度は失われません。
小数点の場合、特に一部の電子商取引 Web サイトに金額などのデータが含まれる場合、フロントエンドで問題が発生する可能性が依然として多くあります。解決策: 小数を整数に代入し (乗算)、それを元の倍数に戻します (倍数で割ります)
// 0.1 + 0.2 (0.1*10 + 0.2*10) / 10 == 0.3 // true
以下は、10 進数の加算、減算、乗算、除算の演算における精度の損失を防ぐために私が書いたオブジェクトです。もちろん、変換された整数は 9007199254740992 を超えることはできません。
/**
* floatObj 包含加减乘除四个方法,能确保浮点数运算不丢失精度
*
* 我们知道计算机编程语言里浮点数计算会存在精度丢失问题(或称舍入误差),其根本原因是二进制和实现位数限制有些数无法有限表示
* 以下是十进制小数对应的二进制表示
* 0.1 >> 0.0001 1001 1001 1001…(1001无限循环)
* 0.2 >> 0.0011 0011 0011 0011…(0011无限循环)
* 计算机里每种数据类型的存储是一个有限宽度,比如 JavaScript 使用 64 位存储数字类型,因此超出的会舍去。舍去的部分就是精度丢失的部分。
*
* ** method **
* add / subtract / multiply /divide
*
* ** explame **
* 0.1 + 0.2 == 0.30000000000000004 (多了 0.00000000000004)
* 0.2 + 0.4 == 0.6000000000000001 (多了 0.0000000000001)
* 19.9 * 100 == 1989.9999999999998 (少了 0.0000000000002)
*
* floatObj.add(0.1, 0.2) >> 0.3
* floatObj.multiply(19.9, 100) >> 1990
*
*/
var floatObj = function() {
/*
* 判断obj是否为一个整数
*/
function isInteger(obj) {
return Math.floor(obj) === obj
}
/*
* 将一个浮点数转成整数,返回整数和倍数。如 3.14 >> 314,倍数是 100
* @param floatNum {number} 小数
* @return {object}
* {times:100, num: 314}
*/
function toInteger(floatNum) {
var ret = {times: 0, num: 0}
if (isInteger(floatNum)) {
ret.num = floatNum
return ret
}
var strfi = floatNum + ''
var dotPos = strfi.indexOf('.')
var len = strfi.substr(dotPos+1).length
var times = Math.pow(10, len)
var intNum = parseInt(floatNum * times + 0.5, 10)
ret.times = times
ret.num = intNum
return ret
}
/*
* 核心方法,实现加减乘除运算,确保不丢失精度
* 思路:把小数放大为整数(乘),进行算术运算,再缩小为小数(除)
*
* @param a {number} 运算数1
* @param b {number} 运算数2
* @param digits {number} 精度,保留的小数点数,比如 2, 即保留为两位小数
* @param op {string} 运算类型,有加减乘除(add/subtract/multiply/divide)
*
*/
function operation(a, b, digits, op) {
var o1 = toInteger(a)
var o2 = toInteger(b)
var max = o1.times > o2.times ? o1.times : o2.times
var result = null
switch (op) {
case 'add':
result = o1.num + o2.num
break
case 'subtract':
result = o1.num - o2.num
break
case 'multiply':
result = o1.num * o2.num
break
case 'divide':
result = o1.num / o2.num
break
}
return result / max
}
// 加减乘除的四个接口
function add(a, b, digits) {
return operation(a, b, digits, 'add')
}
function subtract(a, b, digits) {
return operation(a, b, digits, 'subtract')
}
function multiply(a, b, digits) {
return operation(a, b, digits, 'multiply')
}
function divide(a, b, digits) {
return operation(a, b, digits, 'divide')
}
// exports
return {
add: add,
subtract: subtract,
multiply: multiply,
divide: divide
}
}();
ToFixed は次のように修正されます
// toFixed 修复
function toFixed(num, s) {
var times = Math.pow(10, s)
var des = num * times + 0.5
des = parseInt(des, 10) / times
return des + ''
}上記は JavaScript の数値精度の低下の問題に関するもので、典型的な問題を分析し、数値精度の低下の原因を分析し、解決策も共有します。