ヒルソートを実装する Python のコード例

この記事では主に Python での Hill ソートの実装を紹介します。プログラムされた Hill ソートには一定の参考値があります。興味のある方は参考にしてください。

「挿入ソート」を観察してください。実際、それを見つけるのは難しくありません。 :

データが「5、4、3、2、1」の場合、「順序なしブロック」のレコードを「順序付きブロック」に挿入すると、おそらくクラッシュするため、位置を毎回移動する必要があります。このとき、挿入ソートの効率が想像できます。

シェルはこの弱点に基づいてアルゴリズムを改良し、「減少増分ソート法」と呼ばれるアイデアを組み込んでいます。これは実際には非常に単純ですが、注目すべき点は次のとおりです:

増分はランダムではなく、規則的です。

ヒルソートの時間解析は難しいキーコードの比較回数と記録された動きの数は、特定の状況下では、キーコードの比較回数dの選択に依存します。記録された動きの数を正確に推定できます。最良の増分因子シーケンスを選択する方法をまだ誰も示していません。インクリメンタルファクターの並びは奇数や素数など様々な取り方が可能ですが、インクリメンタルファクター間には1以外の共通因子はなく、最後のインクリメンタルファクターは1でなければならないことに注意してください。ヒルソート法は不安定なソート法です。 まず第一に、増分を取得する方法を明確にする必要があります (ここの写真は他の人のブログのコピーです。増分は奇数ですが、以下のプログラミングでは偶数を使用しています):

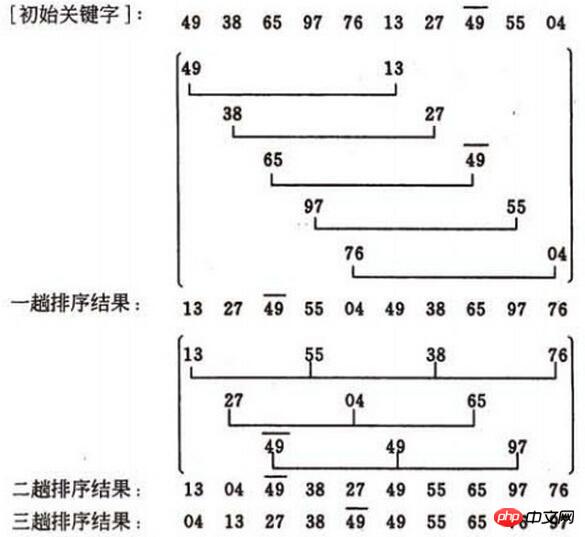
最初の増分を取得する方法は次のとおりです: d=count/2 量 2 番目の増分の方法は次のとおりです: d = (count/2)/2; 最後に、d = 1; に注意してください。画像では、最初の旅行 d1 = 5 、ソート対象の 10 件のレコードを 5 つのサブシーケンスに分割し、それぞれ

します。結果は (13, 27, 49, 55, 04, 49, 38, 65) になります。 , 97, 76)

2 回目のパスでは、d2=3 をインクリメントし、ソート対象の 10 レコードを 3 つのサブシーケンスに分割し、それぞれ直接挿入ソートを実行します。結果は (13, 04, 49, 38, 27, 49, 55, 65, 97, 76)

回 3 パスの増分は d3=1 で、シーケンス全体が直接挿入され、ソートされます。 最終結果

は (04, 13, 27, 38, 49, 49, 55, 65, 76, 97)ここからが重要なポイントです。増分が 1 に減少すると、シーケンスは基本的に順序どおりになり、Hill ソートの最後のパスは直接挿入ソートとなり、最良の状況に近づきます。前のパスでの「マクロ」調整は、最後のパスの前処理とみなすことができ、直接挿入ソートを 1 つだけ行うよりも効率的です。

私はPythonを学習していて、今日はPythonを使用してヒルソートを実装しました。

def ShellInsetSort(array, len_array, dk): # 直接插入排序
 for i in range(dk, len_array): # 从下标为dk的数进行插入排序
 position = i
 current_val = array[position] # 要插入的数

 index = i
 j = int(index / dk) # index与dk的商
 index = index - j * dk

 # while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 # index = index - dk
 # if 0<=index and index <dk:
 # break

 # position>index,要插入的数的下标必须得大于第一个下标
 while position > index and current_val < array[position-dk]:
 array[position] = array[position-dk] # 往后移动
 position = position-dk
 else:
 array[position] = current_val

def ShellSort(array, len_array): # 希尔排序
 dk = int(len_array/2) # 增量
 while(dk >= 1):
 ShellInsetSort(array, len_array, dk)
 print(">>:",array)
 dk = int(dk/2)

if __name__ == "__main__":
 array = [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
 print(">:", array)
 ShellSort(array, len(array))

出力:

>: [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
>>: [13, 27, 49, 55, 4, 49, 38, 65, 97, 76]
>>: [4, 27, 13, 49, 38, 55, 49, 65, 97, 76]
>>: [4, 13, 27, 38, 49, 49, 55, 65, 76, 97]

挿入ソートとは、上の画像の3つの黄色のボックスに数字を挿入してソートすることです。例: 13、55、38、76

[27, 4, 65]、4<27、その後、27 が戻り、最初のボックスが 4 に置き換えられ、データは [4, 27, 65] になります。 ] 、

。挿入する数値の添え字が最初の添え字 1 より大きい場合は、前の数値に戻すことができます。 1 つは、前にデータがある場合です。が挿入する数値より小さい場合は、その後ろにのみ挿入できます。もう 1 つの非常に重要な点は、挿入する数値が以前のすべての数値より小さい場合、挿入する数値の添え字 = 最初の数値の添え字である必要があります。 (この文章は初心者にはあまり理解できないかもしれません...)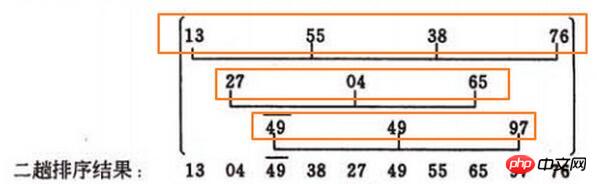

while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 index = index - dk
 if 0<=index and index <dk:
 break

j = int(index / dk) # index与dk的商
index = index - j * dk

ヒルソートの時間計算量は、取得される増分シーケンスの関数であり、正確に分析するのは困難です。一部の文献では、増分シーケンスが d[k]=2^(t-k+1) の場合、ヒル ソートの時間計算量は O(n^1.5),

安定性: 不安定ヒルソート効果:

以上がヒルソートを実装する Python のコード例の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。