忘れられがちな Java 面接の質問のまとめ

静的クラスと静的メソッド

クラスが static として宣言される場合、静的内部クラスというケースが 1 つだけあります。

静的内部クラスは、クラスであるため、実際には通常のクラス（つまり、クラス名がファイル名と同じである必要があるトップレベルのクラス）と同じです。使用したい場合はインスタンス化する必要があります。概念的には、これらは静的 変数 や静的メソッドとは異なります。「静的」という言葉に混同されないでください (すべての静的なものはインスタンス化せずに直接使用できるとは考えないでください。静的内部クラスには違いがあります)。また、静的な内部クラスのみがあり、静的なクラス (トップレベルのクラス) の概念はありません。

例:

public class Singleton{
    private Singleton(){}

    private static class SingletonHolder{
        private final static Singleton instance;
    }

    public Singleton getInstance(){
        return SingletonHolder.instance;
    }
}

静的メソッドは静的メンバーのみにアクセスでき、インスタンス メソッドは静的メンバーとインスタンス メンバーの両方にアクセスできます。静的メソッドがインスタンスのメンバー変数にアクセスできない理由は、インスタンスのメンバー変数は特定のオブジェクトに属しており、静的メソッドの実行時にそのオブジェクトが存在するとは限らないためです。キーワード this は静的メソッドでは使用できません。 Inverted Index

Inverted Index

行列の転置に相当する転置インデックスと訳すと分かりやすいかもしれません。

転置インデックスは、全文検索で文書または文書グループ内の単語の保存場所のマッピングを保存するために使用されるインデックス作成方法です。

Reflection

Reflection

で提供される動的プロキシも非常に強力な機能であり、AOPのメソッドインターセプト機能をネイティブに実装できます。英語のリフレクションという言葉の意味と同じように、リフレクション API を使用することは、水の中の Java クラスの反射を見るようなものです。 Java クラスの内部構造を理解した後は、新しいオブジェクトの作成やオブジェクト内のメソッドの呼び出しなど、Java クラスを操作できるようになります。 この対話方法は、ソース コード内で直接使用する場合と同じ効果がありますが、実行時の柔軟性がさらに高まります。リフレクションを使用する最大の欠点の 1 つは、パフォーマンスの低下です。同じ操作の場合、リフレクション API を使用するのに必要な時間は、直接使用するよりもおそらく 1 ～ 2 桁遅くなります。ただし、現在の JVM 実装では、リフレクション操作のパフォーマンスが大幅に向上しています。

Java リフレクション API の最初の主な機能は、実行時にプログラムの内部構造を取得することです。

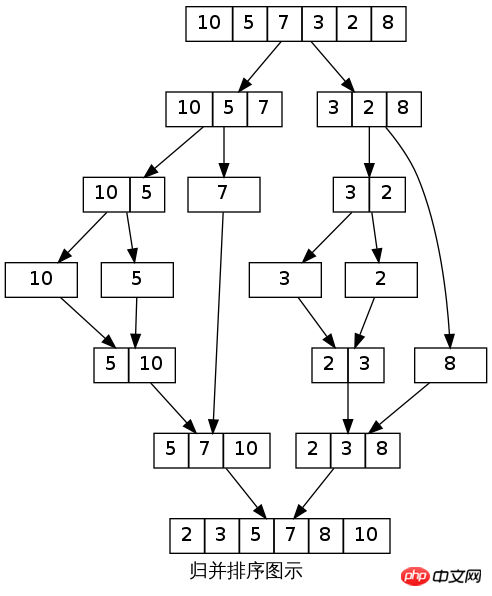
マルチウェイマージアルゴリズム

マージソートも、分割統治法を使用して実装された効果的なソートアルゴリズムであり、1945年に現代のコンピューターの創始者であるジョン・フォン・ノイマンによって発明されました。

マージソートは、多くのソートアルゴリズムの中でも安定したソートであり、非常に効率的です。同時に、マージソートは内部ソートだけでなく外部ソートにも使用できます。

マージソートの考え方は次のとおりです (双方向マージを例に挙げます):

2 つの単語配列をソートします。ソートされた 2 つの単語配列をソートします。
いわゆる N-way マージとは、配列を N 個のサブ配列に分割し、配列をソート
• してからマージすることを意味します。したがって、双方向マージはマージ ソートの最も一般的なケースです。
  例:
凡例

def msort(array):
    length = len(array)
    if length == 1:
        return array
    else:
        mid = length / 2
        left = msort(array[0: mid])
        right = msort(array[mid: length])
        return merge(left, right)

非再帰

def msort(array):
    length = len(array)
    step = 1
    while step < length:
        for left in range(0, length - step, 2 * step):
            result = merge(array[left:left + step],
                           array[left + step: min(left + 2 * step,
             length)])
            array = array[0:left] + result + array[min(left + 2 *
                                                       
           step, length)]
        step = step * 2
    return array

def merge(left, right):
    llen = len(left)
    lcur = 0
    rlen = len(right)
    rcur = 0
    result = []
    while lcur < llen and rcur < rlen:
        lone = left[lcur]
        rone = right[rcur]
        result.append(min(lone, rone))
        if lone < rone:
            lcur += 1
        else:
            rcur += 1
    result += left[lcur:]
    result += right[rcur:]
    return result

• マルチスレッド Java でマルチスレッドを実装するには、Thread クラスを継承する方法と Runnable インターフェースを実装する方法があります。プログラム開発でマルチスレッドである限り、Runnable インターフェースは常に使用されます。主な理由は、Runnable インターフェイスの実装と比較して、Thread クラスの継承には次の利点があるためです。

  1. Java の単一継承機能によって引き起こされる制限を回避できます。コードは複数のスレッドで共有でき、コードとデータは独立しています ;
• 3. 同じプログラム コードを持つ複数のスレッド領域が同じリソースを処理する状況に適しています。

以下は、Runnable インターフェースを実装することによって実装されたマルチスレッド プログラムです。コードは次のとおりです。

以上が忘れられがちな Java 面接の質問のまとめの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。