PHPアルゴリズム学習の動的プログラミング(2)

以前に動的計画の概念と解決手順を簡単に紹介しましたが、勉強中に動的計画の適用範囲が柔軟すぎると感じました。ここで、よくある質問をいくつか取り上げて、さらに練習してみます。

1. 最長共通部分列 (文字列関連)

2 つの文字列が与えられた場合、最長共通部分列 (LCS) を見つけて、LCS の長さを返します。例:
例: "ABCD" と "EDCA" が与えられた場合、LCS は "A" (または D または C) で、1 を返します。
"ABCD" と "EACB" が与えられた場合、LCS は "AC" で返されます。 ２．

アイデア: 長さ m の文字列 a と長さ n の文字列 b、それらの最長共通部分列longest[m][n] は、長さ m-1 の a と長さ n-1 の b によって推定できます。 ] は b[n]、longest[m][n] = longest[m-1][n-1] + 1 に等しい; a[m] が b[n] に等しくない場合、longest[m][ n]=max(最長[m-1][n],最長[m][n-1])。文字列 a または b が空の文字列の場合、その文字列と他の文字列の間の最長共通部分列は 0 でなければなりません。最後の質問の答えは、longest[strlen(a)][strlen(b)] です。
コード:

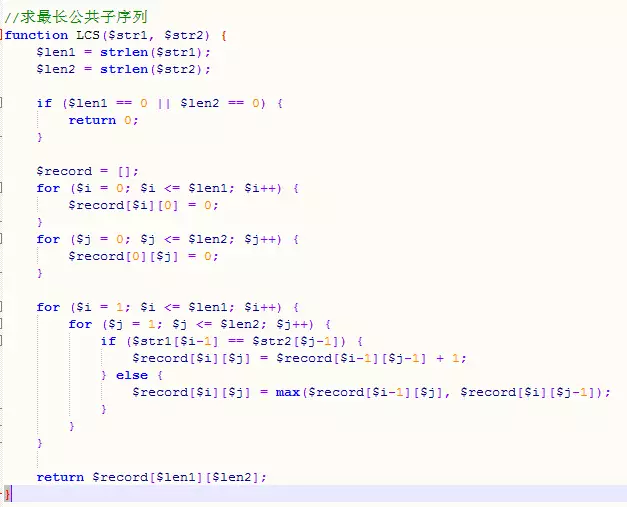
2. 距離の編集 (文字列関連)

2 つの単語 word1 と word2 が与えられた場合、word1 を word2 に変換するための最小操作数を計算します。
文字の挿入、文字の削除、文字の置換の合計3つの操作方法があります。
例: work1="mart" と work2="karma" の場合、3 を返します。

アイデア: 長さ m の文字列 a と長さ n の文字列 b (m と n は両方とも 0 より大きい) の場合、a[m] が b[n] に等しくない場合、最小演算数はa が b になるための =min(a[m-1] が b[n]+1 になるための最小演算数、a[m] が b[n-1]+1 になるための最小演算数、a [m-1] が b になる [n-1]) の最小演算数 a[m] が b[n] に等しい場合、a[m] が b[n になる最小演算数] ] = a[m-1] ～ b[n-1] の最小演算数。
コード:

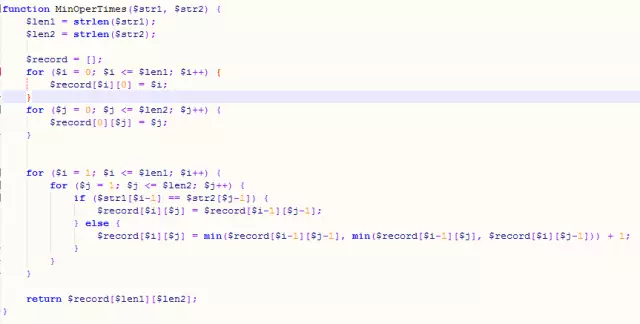
3. ナップザック問題

n個のアイテムの体積A[i]と値V[i]が与えられた場合、それらをサイズmのナップザックに入れ、ロードできる最大の合計はいくらですかそれは価値がありますか？
例: アイテムの体積 [2、3、5、7] と対応する値 [1、5、2、4] の場合、バックパックのサイズが 10 であると仮定すると、ロードできる最大値は 9 です。

アイデア: 空間が v のとき、任意の項目 i について、i を入れることができれば (v がweight[i] 以上である)、このときの v 空間の値 f(v) は次のようになります。 f(v-weight[i ]) + value[i] に等しいため、すべての項目を走査することで、空間が v のときに取得できる最大値を見つけることができます。
コード:

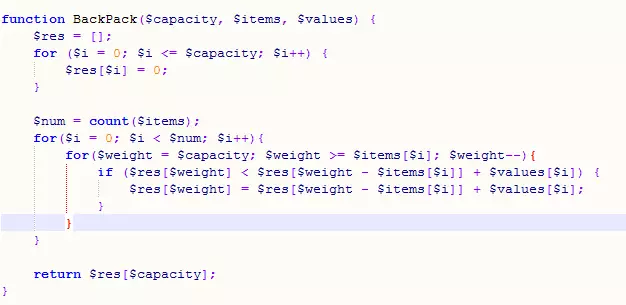
4. インターバル問題 (Google インタビューの質問)

一列に並んだ n 枚のコインがあり、それぞれのコインは異なる価値を持っています。 2 人の出場者は、コインがなくなるまで交互にどちらかの側からコインを受け取ります。獲得したコインの合計値を計算し、最も高い値を獲得したコインが勝ちとなります。先手のプレイヤーが負けるか勝つかを決めてください。
例: 配列 [3,2,2] の場合は true を返し、配列 [1,20,15] の場合は false を返します。

アイデア: 指定された閉区間 (i から j、j が i 以上) では、プレーヤー A には、左または右からコインを受け取る方法が 2 つしかありません。左から見ると、Aが獲得できる最大額面 = 獲得できるコインの額面 + 残りのインターバルの合計額面 - プレイヤーBが残りのインターバルで獲得できる最大額面; Aが右から取る場合と左から取る場合は状況が異なりますが同様です。これから状態遷移方程式を得ることができます。 2 つのループを通じて、長さ n のシーケンス内の i から j までの任意の区間の合計額面と、j=i のときに最初のプレイヤーが取得した最大値 (つまり、i の額面) を取得できます。 -番目のコイン)。
コード:

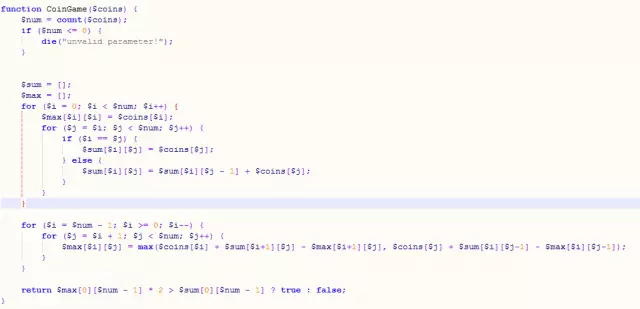
上記は、PHP アルゴリズム学習 - 動的プログラミング (2) の内容です。その他の関連コンテンツについては、PHP 中国語 Web サイト (m.sbmmt.com) に注目してください。