PHPアルゴリズム学習の動的プログラミング

動的計画法は、最適化問題を解決する方法および方法です。最終問題の最適解は、前の部分問題の最適解から導き出すことができます。

動的計画アルゴリズムについては、私は完全に学習していません。私の学習経験を簡単に要約すると、次のようになります。

動的計画の考え方は、再帰と分割統治の考え方を組み合わせたものですが、分割とは何が違うのですか。そして征服とは、動的計画法です。計画と解決では、解決プロセスの各分岐の最適解がステータスを通じて記録されるため、多くの分岐の繰り返し計算が節約されます。

動的プログラミングの最も重要かつ困難な 2 つのステップは、部分問題を記述する状態と状態間の導出関係を見つけることです。

動的計画法を使用する可能性が高い問題: 最大値と最小値を見つける、実行可能な解があるかどうか、実行可能な解の数。

最初に最も一般的な質問に挑戦してみましょう。フィボナッチ数列の特定の位置の値を見つけてください (知らない学生は、Baidu で検索してください)。
分割統治法を適用してコードを解決します

分割統治法を解くプロセスでは、多くの繰り返し操作が行われます。以下の図 3 と図 2 は両方とも 2 回繰り返される操作であり、インデックスが大きくなります。値が大きくなるほど、繰り返される回数が増えます。

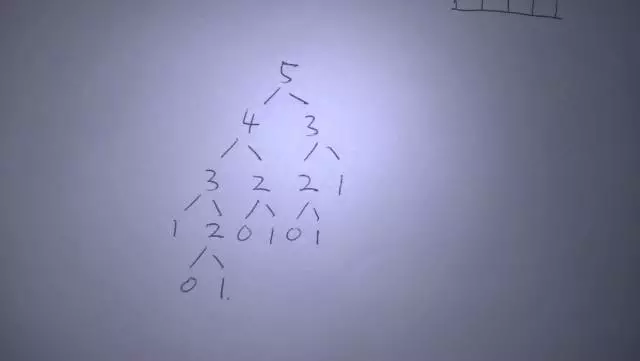
それでは、動的プログラミングを最適化する方法を見てみましょう。

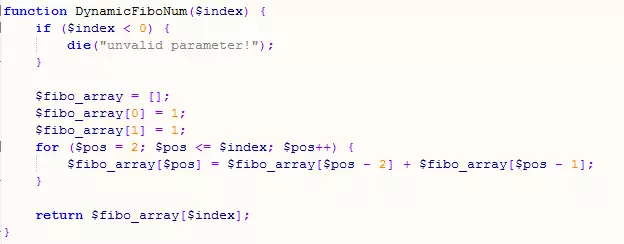
フィボナッチの各位置の値を記録する配列を定義します。これは、状態を定義するのと同じであり、各位置の値は前の 2 つの値の合計に等しく、これは に相当します。状態遷移方程式。
ここで配列を介してステータスを記録するというアイデアは、空間を時間と交換することです。実際、これは私たちが日常の開発で使用するキャッシュ設計と非常に似ています。

まとめ 動的プログラミングの解決策は 4 つのステップに分けることができます:
1. 解決すべき部分問題、つまり状態の定義を決定します。
2. 状態遷移方程式を列挙します。
3. 与えられた条件に従って既知の状態値を初期化します。
4. 最終的な問題解決策を解きます。

もっと面白い問題、階段を上ってみましょう:

上記は、PHP アルゴリズム学習の動的プログラミングの内容です。その他の関連コンテンツについては、PHP 中国語 Web サイト (m.sbmmt.com) を参照してください。 ！