
スパイラル キュー ロジックに基づくスパイラル モーションの実装
スパイラル キュー アルゴリズムの逆の方法により、下図に示すように、2 軸モーターがらせん軌道に沿って移動するように制御されます。
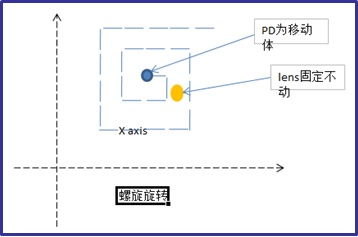
1. スパイラルキューアルゴリズムの解析
下の写真はスパイラルキューです。 1 の座標は (0, 0)、x 方向は右が正、y 方向は下が正であるとします。たとえば、7 の座標は (-1, -1) で、 の座標は次のようになります。 2 は (1, 0) です。プログラミングを使用すると、任意の点の座標 (x, y) を入力し、対応する数値を出力できます。 (ネットより転載)
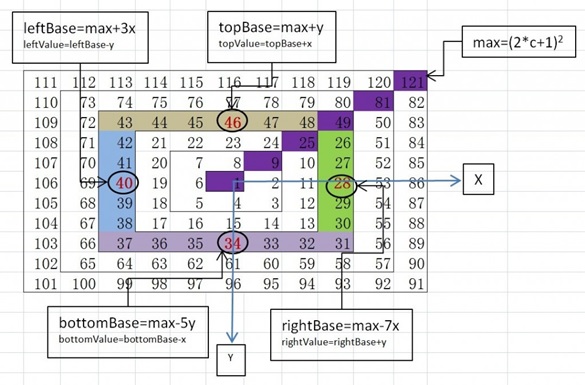
各円の最大値max=(2*c+1)(2*c+1)、cは内側から外側までの円の数です。
これらの参考値と最大の差は、1C(上)、3C(左)、5C(下)、7C(右)(Cは現在の周回数を表します)、上側と下側で、 y 座標は円の数 (つまり C=y) を表し (または等しい)、左側と右側では、x 座標は円の数 (つまり C=x) を表します (または等しい)。 。したがって、先ほどの差分は座標で1y、3x、5y、7xと表すことができます。
コード実装:
private static Object spiral(int x, int y)
{
int c = max(abs(x), abs(y));// 当前坐标所在圈
int max = (c * 2 + 1) * (c * 2 + 1);// 当前圈上最大值
if (y == -c) { // 上边
return max + (x + y);
} else if (x == -c) {// 左边
return max + (3 * x - y);
} else if (y == c) {// 下边
return max + (-x - 5 * y);
} else {// 右边
return max + (-7 * x + y);
}
}2. スパイラルモーション
まず、PD の論理位置を表す座標演算をカスタマイズします。
struct Coordinate
{ public int X; public int Y; public Coordinate(int a, int b)
{
X = a;
Y = b;
} public static bool operator ==(Coordinate loc1, Coordinate loc2)
{ return (loc1.X == loc2.X) && (loc1.Y == loc2.Y);
} public static bool operator !=(Coordinate loc1, Coordinate loc2)
{ return !(loc1 == loc2);
} public override bool Equals(object loc)
{ return this == (Coordinate)loc;
} public override int GetHashCode()
{ return base.GetHashCode();
} public static Coordinate operator -(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X - loc2.X, loc1.Y - loc2.Y);
} public static Coordinate operator +(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X + loc2.X, loc1.Y + loc2.Y);
} public override string ToString()
{ return "(" + X + "," + Y + ")";
}
}次に、逆の方法を使用して、ステップ数に基づいて X、Y 座標を計算します。
public Coordinate ToLocation(int step, int pulse)
{
int c = (int)Math.Ceiling((Math.Sqrt(step) - 1) / 2);
int max = (int)Math.Pow(2 * c + 1, 2);
int x, y;
y = -c;//top
x = -(max + y - step);
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = -c;//left
y = max + 3 * x - step;
if (Math.Abs(y) <= Math.Abs(x))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
y = c;//bottom
x = max - 5 * y - step;
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = c;//right
y = -(max - 7 * x - step);
this.location.X = x * pulse;
this.location.Y = y * pulse;
//LocChange();
return this.location;
}最後に、座標の変更に応じた動きが実現されます。
public void Start()
{
Coordinate moveToLoc, currentLoc, deltaLoc;
currentLoc = ToLocation(1, 0);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the start location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "begin to move... ");
log.SaveLogToTxt(logInfo);
for (int step = 1; step <= this.roMaxStep[0]; step++)
{
moveToLoc = ToLocation(step + 1, this.roPulse[0]);
deltaLoc = moveToLoc - currentLoc;
logInfo = string.Format("{0}: step{1}{2}{3}...", DateTime.Now.ToString("HH:mm:ss"), step + " ", "move to ", moveToLoc.ToString());
log.SaveLogToTxt(logInfo);
bool moveX = card.MoveX(deltaLoc.X);
bool moveY = card.MoveY(deltaLoc.Y);
if (moveX == false || moveY == false)
//throw error
return;
currentLoc = moveToLoc;
//if RES > RoRESTarget
//break;
}
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "move done");
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the current location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
}上記は、0-Spiral Queue と Spiral Movement の独習 C#07 の内容です。その他の関連コンテンツについては、PHP 中国語 Web サイト (m.sbmmt.com) をご覧ください。