πは、数え切れないほどの人が従う本当に魔法の数字です。永遠に繰り返される無理数の何がそんなに魅力的なのか、私にはよくわかりません。私は、πの計算、つまりπの値を計算することが楽しいと思っています。 πは無理数なので無限大です。これは、π の計算は単なる近似値にすぎないことを意味します。あなたが 100 桁を計算する場合、私は 101 桁を計算することができ、より正確になります。これまでのところ、最も正確な π を計算するためにスーパーコンピューターを選んでいる人もいます。極端な値には、円周率 5 億桁の計算も含まれます。 100 億桁の π を含むテキスト ファイルをオンラインで見つけることもできます (注意してください。このファイルのダウンロードには時間がかかる場合があり、通常のメモ帳アプリケーションでは開くことができません)。私にとって、Python の簡単な数行で π を計算する方法に興味があります。
math.pi 変数はいつでも使用できます。これは標準ライブラリに含まれているため、自分で計算する前に使用する必要があります。 実際に、これを使用して精度を計算します。まず、円周率を計算する非常に簡単な方法を見てみましょう。いつものように、私は Python 2.7 を使用しますが、同じアイデアとコードが異なるバージョンに適用される可能性があります。私たちが使用するアルゴリズムのほとんどは、Pi WikiPedia ページから取得して実装されています。以下のコードを見てみましょう:
importsys
importmath
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=1.0
b=1.0/math.sqrt(2)
t=1.0/4.0
p=1.0
foriinrange(int(sys.argv[1])):
at=(a+b)/2
bt=math.sqrt(a*b)
tt=t-p*(a-at)**2
pt=2*p
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(math.pi-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])これは、必要に応じてダウンロード、実行、変更、他の人と共有できる非常にシンプルなスクリプトです。次のような出力が表示されます。
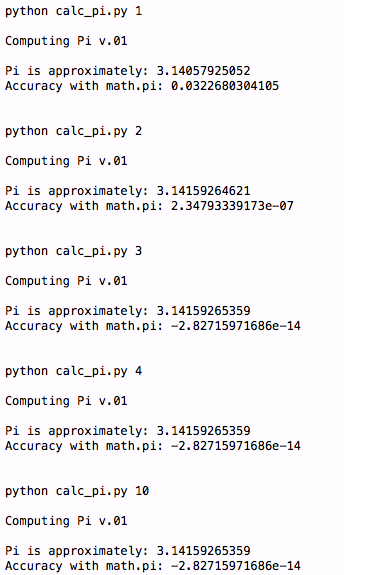
n が 4 より大きいにもかかわらず、Pi への近似の精度があまり改善されていないことがわかります。 nの値が大きくなっても同じこと（円周率の近似精度は上がらない）が起こると推測できます。幸いなことに、この謎を解決する方法は複数あります。 Python Decimal (10 進数) ライブラリを使用すると、Pi を近似するためのより精度の高い値を取得できます。ライブラリ関数がどのように使用されるかを見てみましょう。この簡素化されたバージョンでは、11 桁を超える数値を取得できますが、通常は Python の浮動小数点数より精度が低くなります。 Python Decimal ライブラリの例を次に示します。
これらの数値を参照してください。間違っている！ 3.14 だけを入力したのに、なぜジャンクが発生したのでしょうか? これはメモリジャンクです。 簡単に言うと、Python は必要な 10 進数に加えて、少し追加の値を提供します。 精度が最初の以前のジャンク数値よりも小さい限り、計算には影響しません。 getcontext().prec を設定することで、必要な桁数を指定できます。やってみよう。
とても良いです。 次に、これを使用して、前のコードをより適切に近似できるかどうかを確認してみましょう。 さて、私は通常「 from library import * 」を使用することに反対しますが、この場合はコードがより美しく見えます。
importsys
importmath
fromdecimalimport*
defmain(argv):
iflen(argv) !=1:
sys.exit('Usage: calc_pi.py <n>')
print'\nComputing Pi v.01\n'
a=Decimal(1.0)
b=Decimal(1.0/math.sqrt(2))
t=Decimal(1.0)/Decimal(4.0)
p=Decimal(1.0)
foriinrange(int(sys.argv[1])):
at=Decimal((a+b)/2)
bt=Decimal(math.sqrt(a*b))
tt=Decimal(t-p*(a-at)**2)
pt=Decimal(2*p)
a=at;b=bt;t=tt;p=pt
my_pi=(a+b)**2/(4*t)
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately: "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if__name__=="__main__":
main(sys.argv[1:])出力結果:
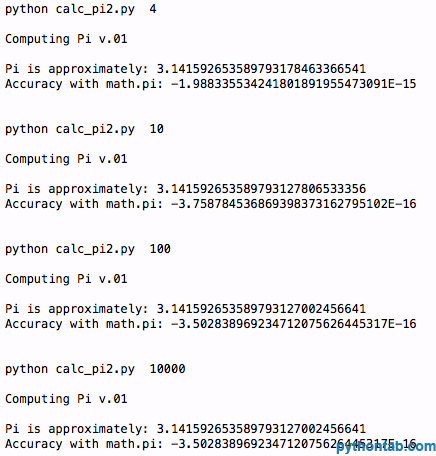
わかりました。より正確ですが、多少の四捨五入があるようです。 n = 100 と n = 1000 では、同じ精度が得られます。何をするべきだろう？さて、数式の話に移りましょう。これまでのところ、円周率を計算する方法は、その部分を加算することによって行われてきました。円周率の計算に関する DAN の記事からコードを見つけました。彼は、次の 3 つの公式を使用することを提案しました:
Bailey-Borwein-Plouffe の公式
Bellard の公式
Chudnovsky アルゴリズム
Bailey-Borwein-Plouffe の公式から始めましょう。次のようになります:
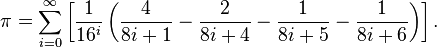
コードでは次のように記述できます:
import sys
import math
from decimal import *
def bbp(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(1)/(16**k))*((Decimal(4)/(8*k+1))-(Decimal(2)/(8*k+4))-(Decimal(1)/(8*k+5))-(Decimal(1)/(8*k+6)))
k+=1
return pi
def main(argv):
if len(argv) !=2:
sys.exit('Usage: BaileyBorweinPlouffe.py <prec> <n>')
getcontext().prec=(int(sys.argv[1]))
my_pi=bbp(int(sys.argv[2]))
accuracy=100*(Decimal(math.pi)-my_pi)/my_pi
print"Pi is approximately "+str(my_pi)
print"Accuracy with math.pi: "+str(accuracy)
if __name__=="__main__":
main(sys.argv[1:])「ラッパー」コードはさておき、BBP(N) の関数が本当に必要なものです。 N を大きくするほど、また getcontext().prec に設定する値が大きくなるほど、計算がより正確になります。コードの結果をいくつか見てみましょう:
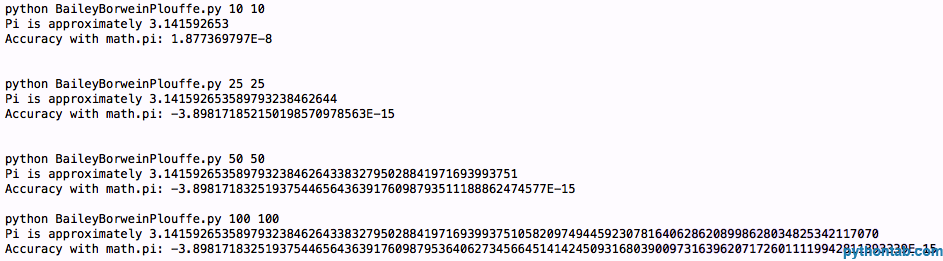
これは大量のデジタルビットです。以前ほど正確ではないことがわかります。したがって、次の公式、Bellah の公式に進み、できれば精度を高める必要があります。次のようになります:
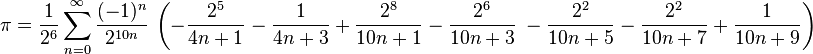
変換式のみを変更し、コードの残りの部分は同じままです。 Python で実装された Bella の数式をダウンロードするには、ここをクリックしてください。 bellards(n) を見てみましょう:
def bellard(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k/(1024**k))*( Decimal(256)/(10*k+1)+Decimal(1)/(10*k+9)-Decimal(64)/(10*k+3)-Decimal(32)/(4*k+1)-Decimal(4)/(10*k+5)-Decimal(4)/(10*k+7)-Decimal(1)/(4*k+3))
k+=1
pi=pi*1/(2**6)
return pi出力:
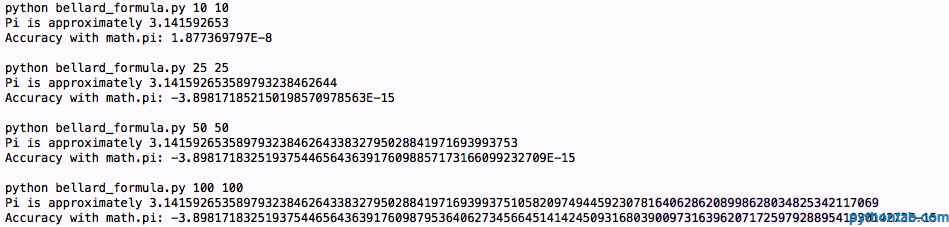
哦，不，我们得到的是同样的精度。好吧，让我们试试第三个公式， Chudnovsky 算法，它看起来是这个样子：
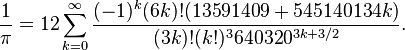
再一次，让我们看一下这个计算公式（假设我们有一个阶乘公式）。 点击这里可下载用 python 实现的 Chudnovsky 公式。
下面是程序和输出结果：
def chudnovsky(n):
pi=Decimal(0)
k=0
while k < n:
pi+=(Decimal(-1)**k)*(Decimal(factorial(6*k))/((factorial(k)**3)*(factorial(3*k)))*(13591409+545140134*k)/(640320**(3*k)))
k+=1
pi=pi*Decimal(10005).sqrt()/4270934400
pi=pi**(-1)
return pi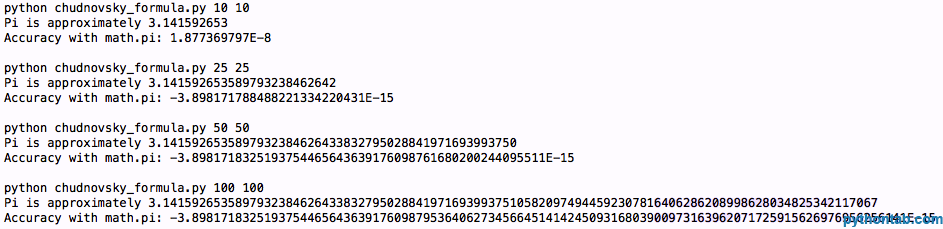
所以我们有了什么结论？花哨的算法不会使机器浮点世界达到更高标准。我真的很期待能有一个比我们用求和公式时所能得到的更好的精度。我猜那是过分的要求。如果你真的需要用PI，就只需使用math.pi变量了。然而，作为乐趣和测试你的计算机真的能有多快，你总是可以尝试第一个计算出Pi的百万位或者更多位是几。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
