マトリックスはわかりにくいですが、見方を変えると違うのかもしれません。
数学を学ぶとき、私たちは学んだ知識の難しさと抽象性にイライラすることがよくありますが、視点を変えるだけで、問題に対するシンプルで直感的な解決策を見つけることができることがあります。たとえば、私たちが子供の頃に二乗和 (a+b)² の公式を習ったとき、それがなぜ a²+2ab+b² に等しいのか理解できなかったかもしれません。この本を読んで、先生は私たちにこのように覚えるように言いました。ある日、このアニメーションを見るまでは、
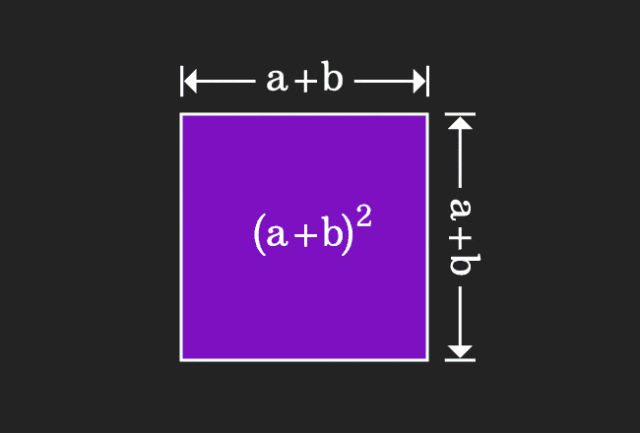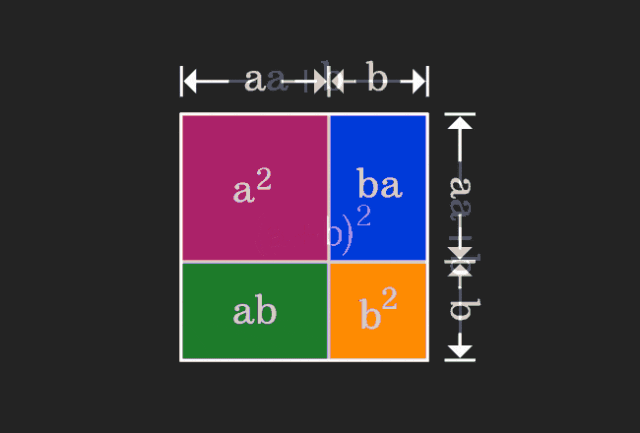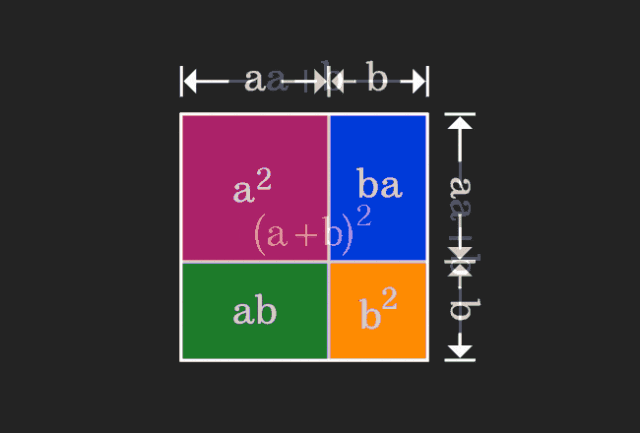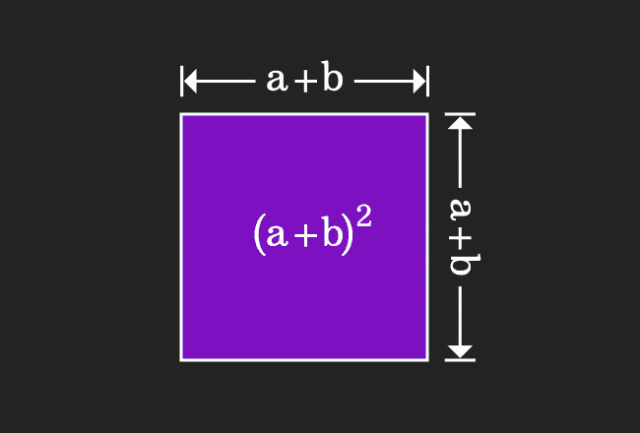
私はそれを幾何学的な観点から理解できることに突然気づきました。
さて、この啓発的な感覚が再び現れました。非負行列は、対応する有向グラフに等価的に変換できます。
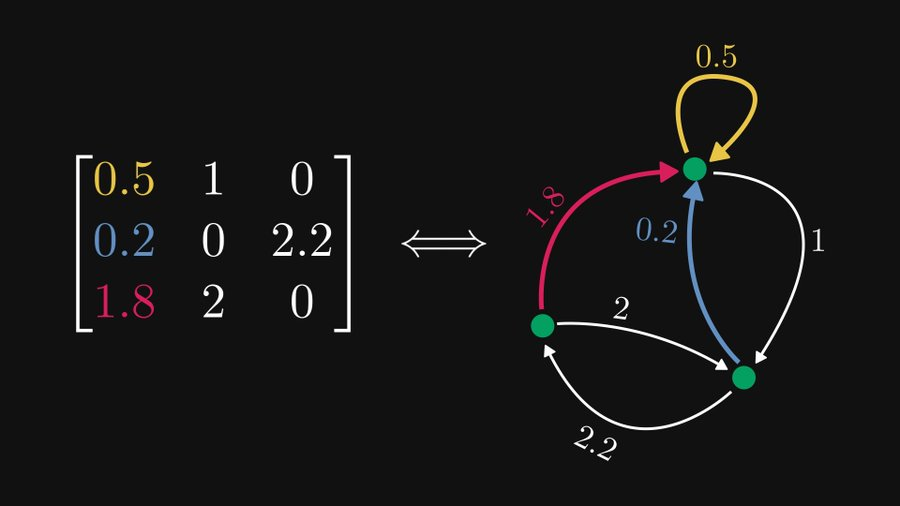
下の図に示すように、左側の 3×3 行列は、実際には右側の 3 つのノードを含む有向グラフとして等価に表すことができ、この表現は行列理論とグラフ理論の両方に非常に役立ちます。
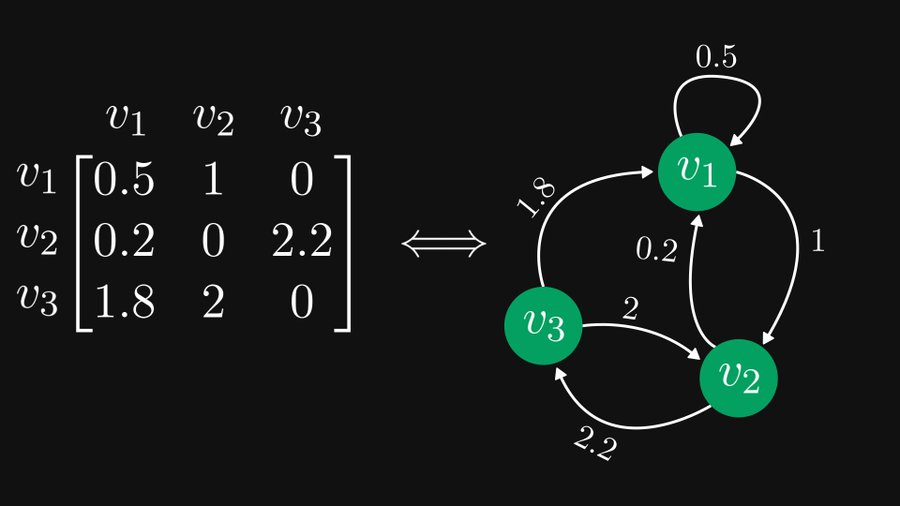
この例は、誰もが数学を利用できるようにすることに尽力している数学者、Tivadar Danka によるものです。自称「混沌とした善良な」数学者は、一連のツイートやブログ投稿で、行列とグラフのこの等価性とその使用法を生き生きと紹介しました。現在までに、このツイートは 200 万回以上読まれ、3,200 件以上のリツイートと 9,100 件以上のお気に入りが登録されています。
行列と有向グラフの価数
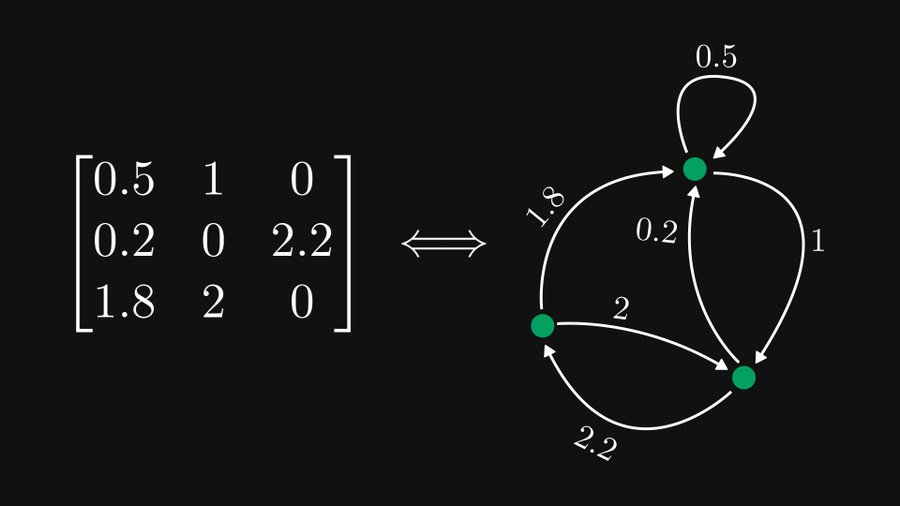
上の例に示すように、各行をノードとして扱う場合、各要素は有向エッジと重み付きエッジとして表すことができます。もちろん、0 要素は無視できます。要素が行 i、列 j に位置する場合、それはノード i からノード j までのエッジに対応します。
これは一見複雑に見えるかもしれませんが、最初にノードの 1 つを見てみましょう。
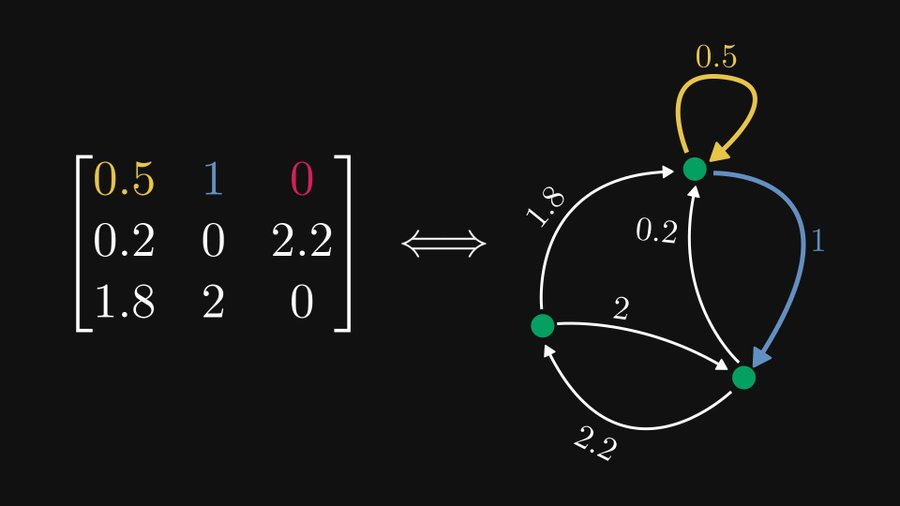
図に示すように、この 3×3 行列の場合、行 1 は最上位のノード (ここではノード 1 と呼びます) に対応します。これには 3 つの要素が含まれていますが、そのうちの 1 つは 0 であるため、このノードは 2 つの要素を拡張します。エッジ。黄色のエッジは (1,1) の要素 0.5 を表すため、重み 0.5 でそれ自体を指す有向エッジです。同様に、青いエッジはノード 2 を指すエッジで、重みは 1 です。
このようにして、行列の i 番目の列が i 番目のノードを指すすべてのエッジに対応していることを分析できます。
この同等の表現は何に使われるのでしょうか?
非負行列と有向グラフの間のこの等価性は、行列とその演算をより深く理解するのに役立つだけでなく、一部の計算プロセスを簡素化するのにも役立ちます。これは、新しい観点から理解する図から始めるのにも役立ちます。
たとえば、行列の累乗はグラフのウォークに対応します。
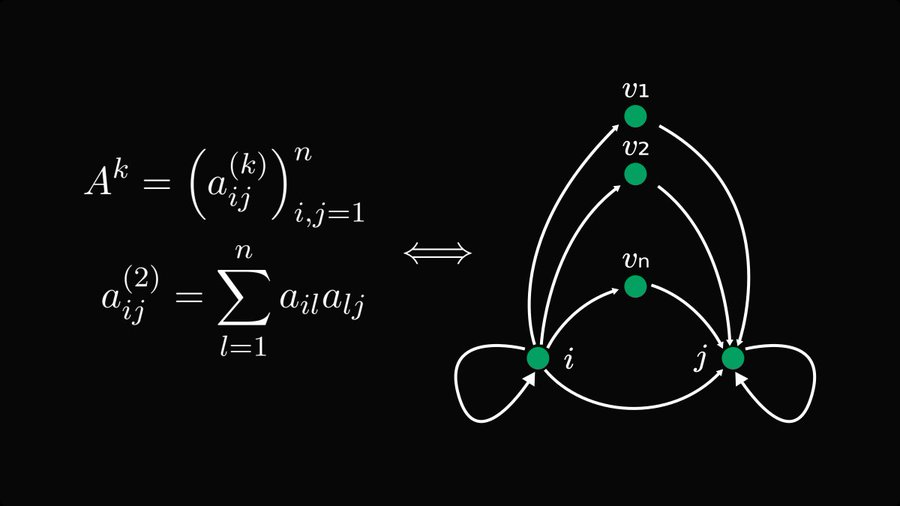
上の図に示すように、n×n 正方行列 A の k 乗について、各要素の合計プロセスには、考えられるすべての k ステップ ウォークが組み込まれます。
たとえば、上記の 3×3 行列の 2 乗を計算したいとします。
行列の乗算を使用する場合は、次のように計算する必要があります:
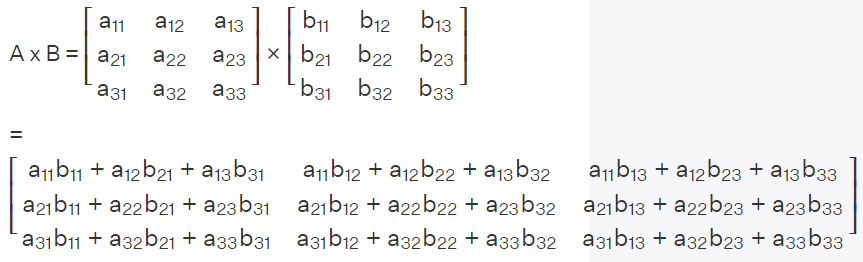
演算結果の最初の要素については、結果 = 0.5×0.5+1×0.2+0×1.8を得ることができます。 = 0.45。最後に、次のように完全な結果を得ることができます:
しかし、上記のグラフウォーキング方法を使用すると、パスを歩くことによって結果を得ることができます。同様に、結果行列の最初の要素については、a_{1,l}→a_{l,1}を満たす 2 ステップの歩行パスをすべて合計する必要があります。
ただし、この有向グラフがマルコフ連鎖の状態を表す場合、その遷移確率行列の二乗は本質的に、連鎖が 2 ステップ後に特定の状態に到達する確率を表します。
それだけでなく、グラフを使用して行列を表すことで、非負の行列の構造を深く理解することもできます。これを行うには、まず「強く接続されたコンポーネント」の概念を理解する必要があるとダンカ氏は言いました。
強連結成分
強連結成分とは何ですか?有向グラフの場合、グラフ内の他のすべてのノードにすべてのノードから到達できる場合、グラフは強く接続されていると言えます。以下に示すように。
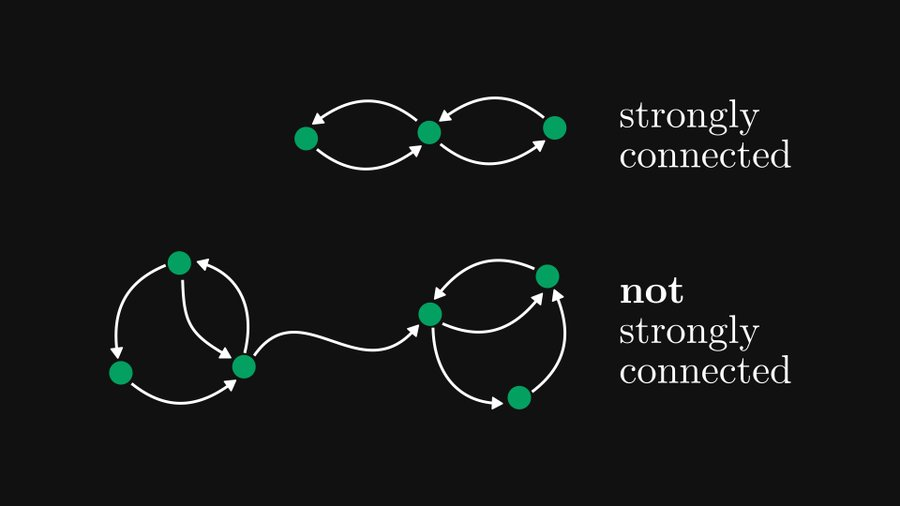
強連結成分とは、有向グラフ内の強連結性を実現できる部分/部分グラフを指します。以下の図に示すように、左右には強連結成分が存在しますが、中央の白いエッジはどの強連結成分にも属していません。
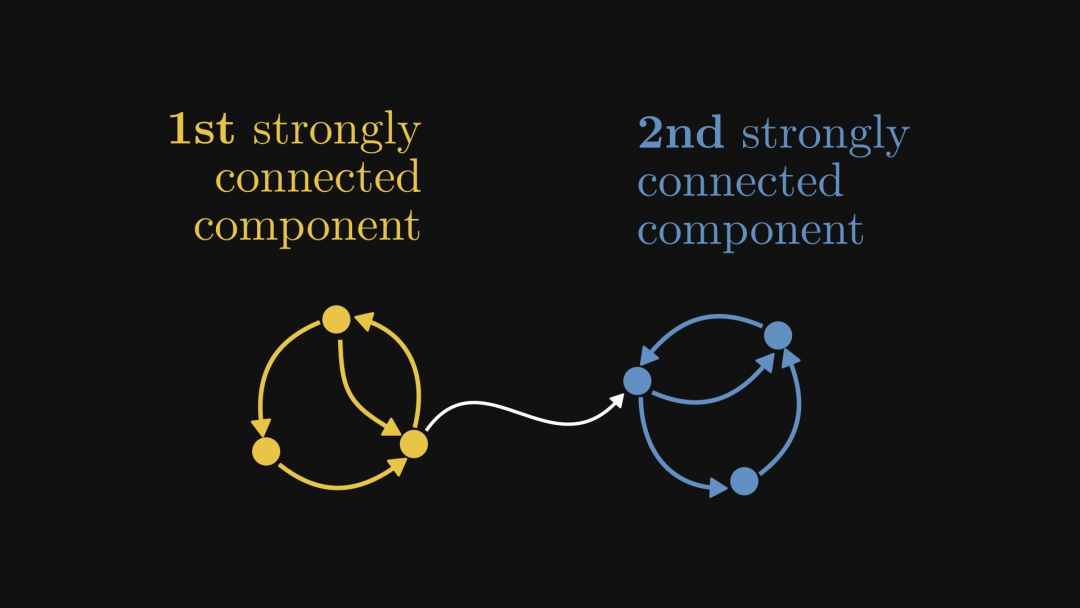
下の図は別の例を示しており、黄色の部分が強連結成分です:
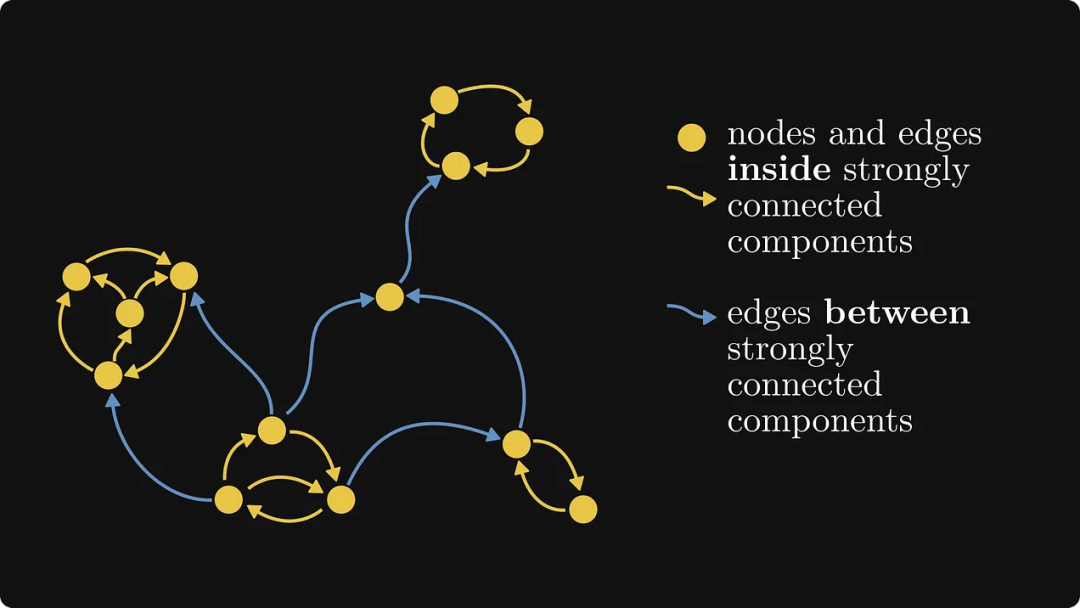
強連結グラフに対応する行列は既約行列ですが、非負行列内の他のすべての行列はは可約行列です。
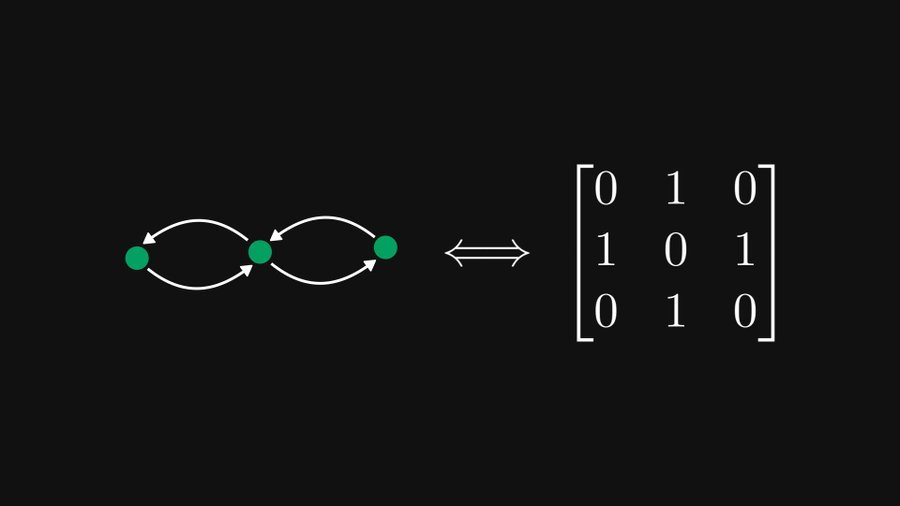
ダンカが例をあげて説明します。 (わかりやすくするために、例のすべての重みは単位重みですが、実際には、これらの重み値は負でない任意の値にすることができます。)
強く接続された成分を含むが強く接続されていないこのグラフを転写してみましょうそれ自体を対応する行列形式に変換します:
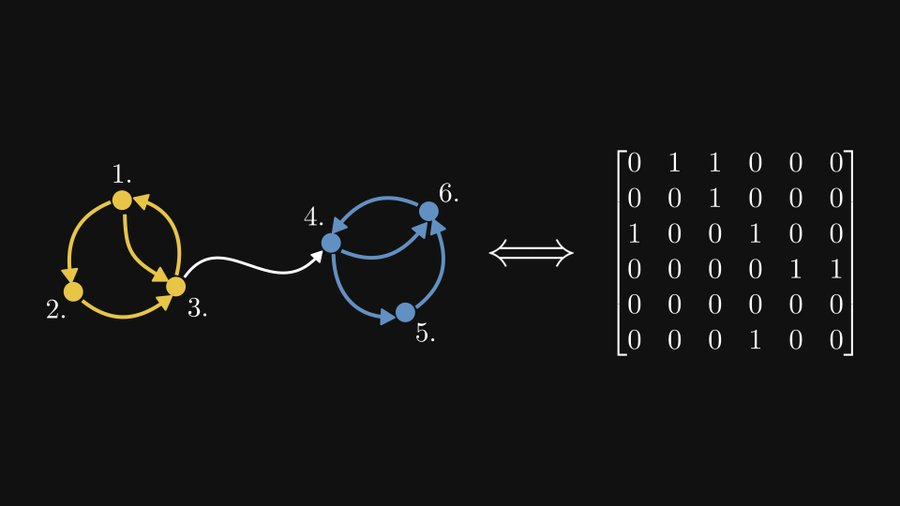
そして、この行列は可約行列です。
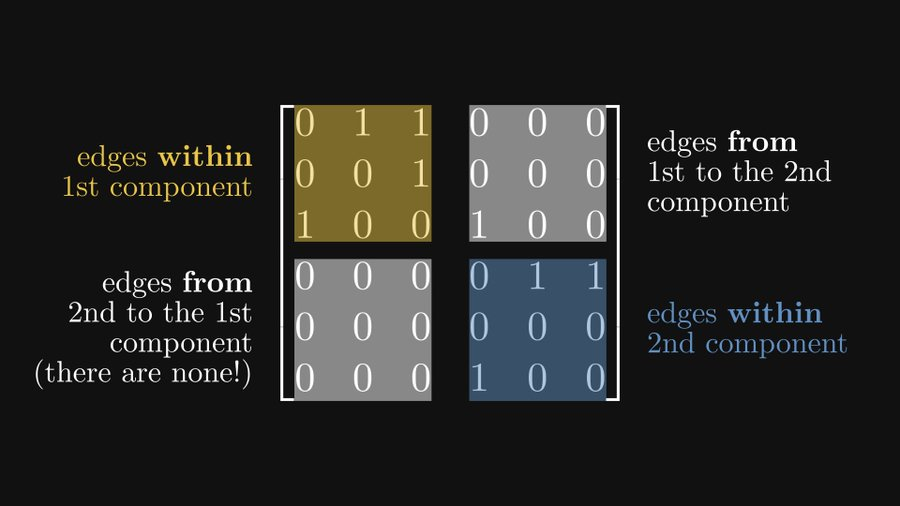
主対角線上の 2 つの部分行列は、それぞれ 2 つの強連結成分を表しており、右上の部分行列は、最初の強連結成分から 2 番目の強連結成分までのエッジを表していることがわかります。左下は、2 番目の強連結成分から最初の強連結成分へのエッジを表します (そのようなエッジはないため、すべて 0 になります)。
このブロック行列の記述形式は、フロベニウス正規形式と呼ばれます。
そこで、当然のことながら、非負行列をフロベニウス正規形行列に変換できるか?と尋ねます。
有向グラフを使用して非負行列を表すと、答えが「はい」であることが簡単にわかります。非負行列を表す有向グラフは、互いに接続された強連結成分として表すことができるためです。このプロセスは非常に簡単です:
非負行列に対応する有向グラフを構築します
各ノードにラベルを付けるより良い方法に変更します。
以上です！
それでは、これより良い方法は何でしょうか?上記の例に基づいて、プロセスを見てみましょう。
まず、以下の図に示すように、強く接続された各コンポーネントを 1 つのオブジェクトに融合します。現時点では、強く接続された各コンポーネントをブラック ボックスとして扱うことができます。内部構造は気にせず、外部接続のみを気にします。
次に、この新しいグラフで、出力エッジのみを持ち、入力エッジを持たないコンポーネントを見つける必要があります。この特定の例では 1 つだけあり、それに番号 0 のラベルを付けます。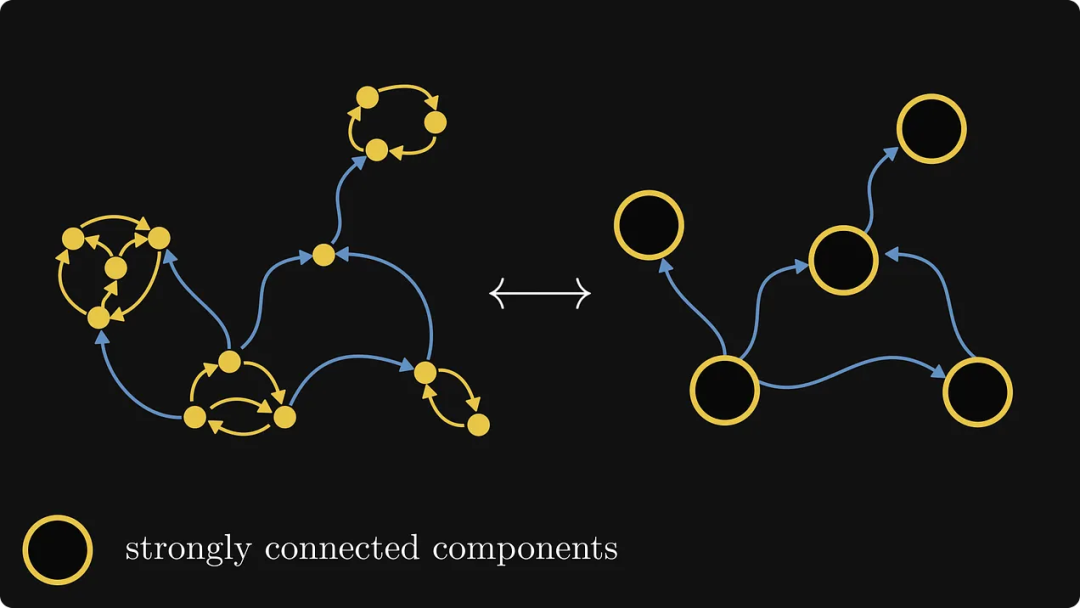
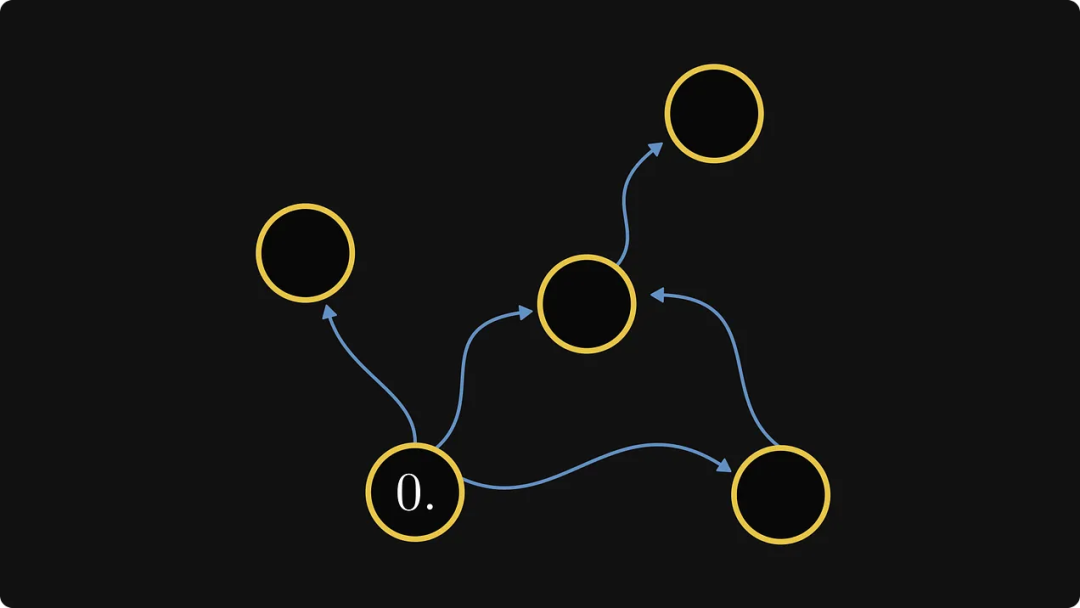
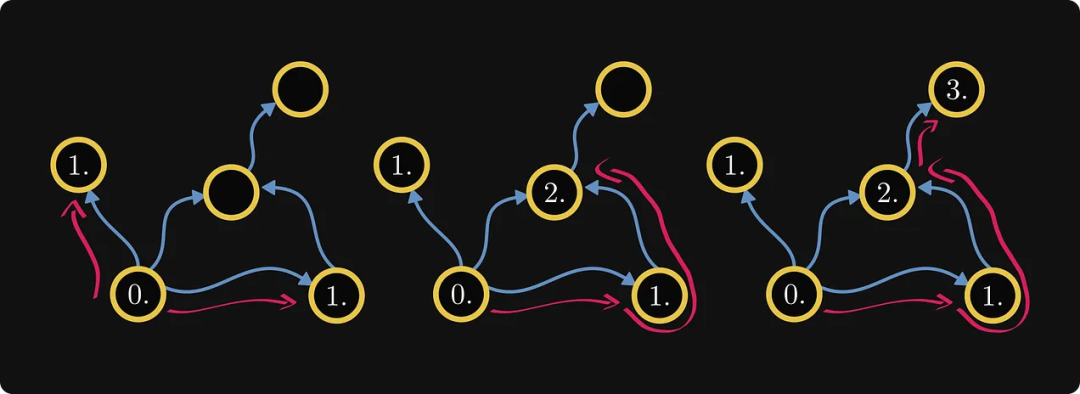
실제로 이는 구성 요소의 순서를 정의합니다. 다음으로, 각 구성 요소의 내부 노드에 레이블을 지정합니다.
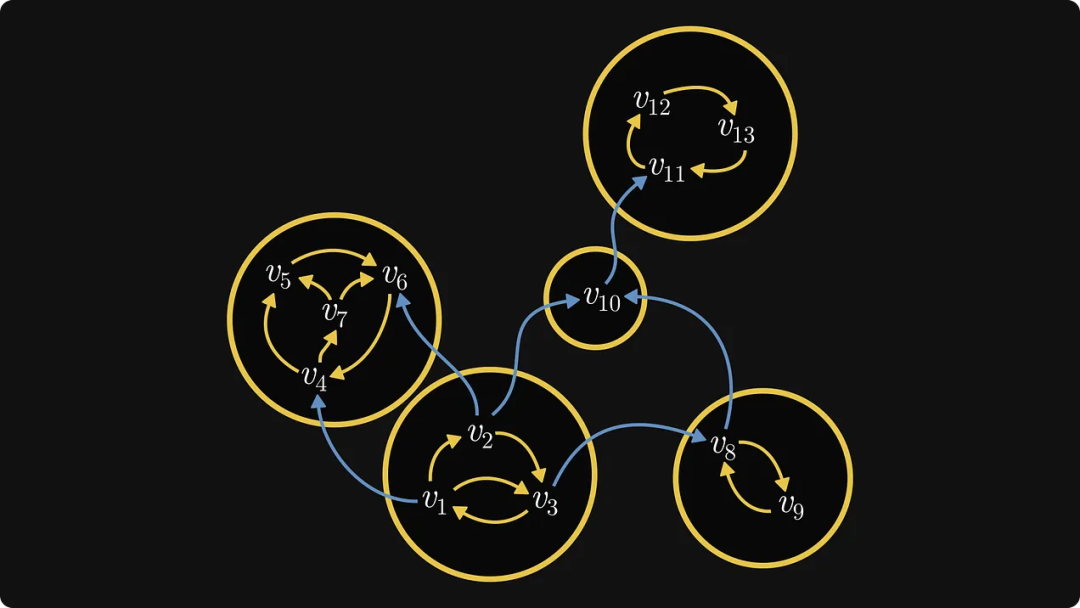
그래프 자체가 행렬에서 나온 경우 이러한 레이블 재지정 프로세스로 인해 Frobenius 정규 행렬이 생성될 수 있습니다!
실제로 이러한 재라벨링 과정은 순열 행렬 P를 사용하여 원래 행렬을 변환하는 것이며, 순열 행렬은 여러 전치 행렬의 곱으로 구성됩니다.
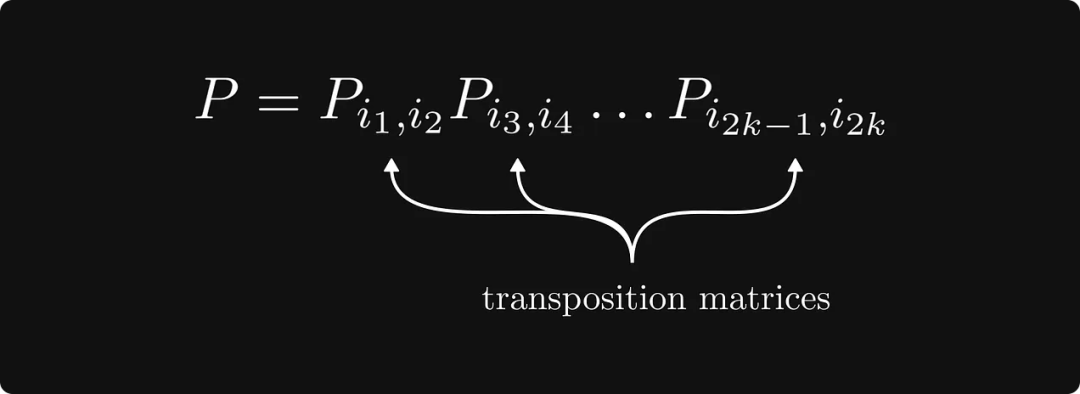
다음은 정리의 완전한 형태입니다.
물론 행렬을 표현하기 위해 그래프를 사용하는 것은 이보다 훨씬 더 뛰어납니다. 예를 들어 행렬의 고유값을 사용할 수도 있습니다. 그래프의 고유값을 정의합니다. 실제로 이러한 사고 방식이 스펙트럼 그래프 이론이라는 연구 분야를 탄생시켰습니다.
결론
분명히 행렬과 그래프의 이러한 등가 관계는 그래프 이론 연구에 도움이 될 뿐만 아니라 선형 대수학의 계산 및 분석에 대한 새로운 관점을 제공합니다. 또한 몇 가지 중요한 실제 용도가 있습니다. 예를 들어, DNA 데이터는 행렬이나 그래프 형태로 표현되는 경우가 많습니다.
또한 우리 모두는 현재 대형 모델 AI에서 행렬 연산의 중요성을 알고 있으며, 지식 그래프로 표현되는 그래프도 검색 강화 검색과 같은 기술을 통해 현재 AI의 중요한 동인이 되고 있습니다. 이 둘을 연결하면 AI 해석 가능성과 그래프 인공 지능에 새로운 돌파구가 생길 수 있습니다. 최소한 이것은 우리가 선형 대수학을 더 잘 배우는 데 도움이 됩니다.
사실 위 내용은 Tivadar Danka가 집필한 책 "기계 학습의 수학"에서 발췌한 것입니다. 이 책은 머신러닝과 관련된 수학적 지식을 단순한 수준부터 심층적인 수준까지 소개하여 독자들이 무슨 일이 일어나고 있는지, 왜 일어나는지 진정으로 이해할 수 있도록 해줄 것이며, 단카는 이 책이 “머신러닝 학습을 위한 최고의 리소스”가 될 것이라고 자신있게 선언합니다. 현재 그는 온라인으로 두 장의 미리보기를 공개했습니다. 관심 있는 독자는 https://tivadardanka.com/mathematics-of-machine-learning-preview/
를 방문하세요.以上が行列とグラフの間には等価関係があるということを、ライン生成を学んでいたときになぜ知らなかったのでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
