パス計画の概要: サンプリング、検索、最適化に基づいてすべて完了しました。

1 意思決定制御と動作計画の概要

現在の意思決定制御方法は、逐次計画、行動認識型計画、およびエンドツーエンド計画の 3 つのカテゴリに分類できます。

• 逐次計画: 最も伝統的な方法であり、知覚、決定、制御の3つの部分が比較的明確です。
• 行動を意識した計画: 最初の方法と比較して、ハイライトは次のとおりです。人間と機械のコラボレーションの導入 運転、車両と道路のコラボレーション、および外部動的環境に対する車両のリスク推定
• エンドツーエンドの計画: 大量のデータ トレーニングの助けを借りて、DL および DRL テクノロジーを使用して、画像などの感覚情報からハンドル角度などの車両制御入力までの情報を統合するリレーションシップは、現在最も一般的な手法の 1 つです。

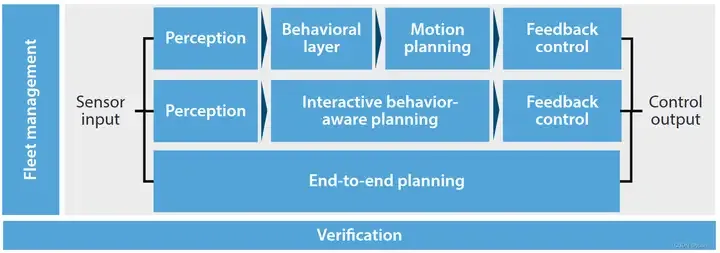
この記事では、逐次計画を紹介し、意思決定制御シーケンス全体に従って自動運転車の知覚制御プロセスを説明し、最後に上記で解決すべき問題を簡単にまとめます。

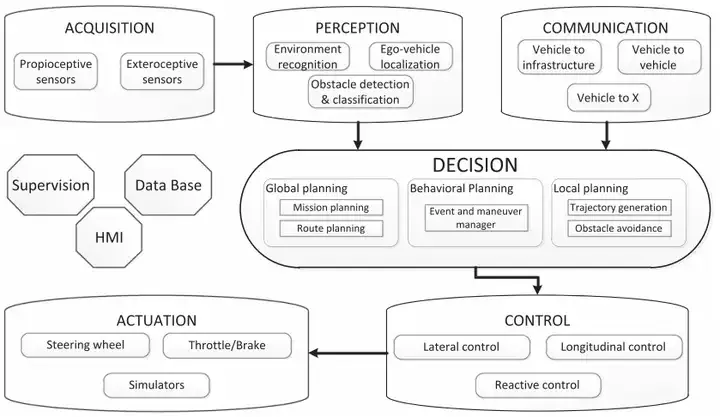
自動運転車両の制御アーキテクチャ

2 経路計画の概要

の一連の計画プロセスは、経路計画->意思決定プロセス->車両制御として簡単にまとめられています。この記事で説明する計画は、最初のステップと 3 番目のステップに属します。

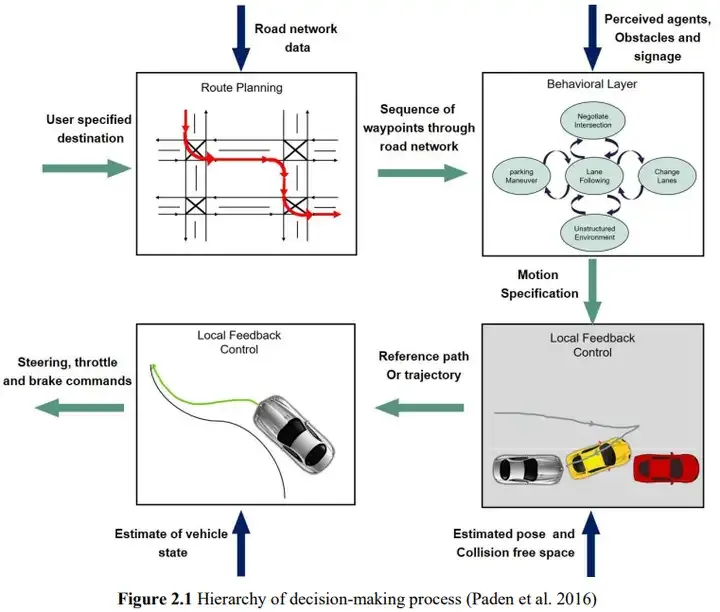
//m.sbmmt.com/link/aa7d66ed4b1c618962d406535c4d282a

無人車両の軌道生成の問題には直接軌道生成法とpath-veの2種類がある位置分解法 、最初のタイプと比較して、パス速度の難易度が低いため、より一般的に使用されます。

2.1 経路計画の種類

経路計画は、PRM および RRT に代表される サンプリング に基づくアルゴリズム、A* および D* に代表される search に基づくアルゴリズム、軌道生成の 4 つの主要なカテゴリに分類できます。 β-スプライン曲線で表される 補間 フィッティングに基づくアルゴリズムと、MPC で表されるローカル パス プランニングの 最適 制御アルゴリズム。

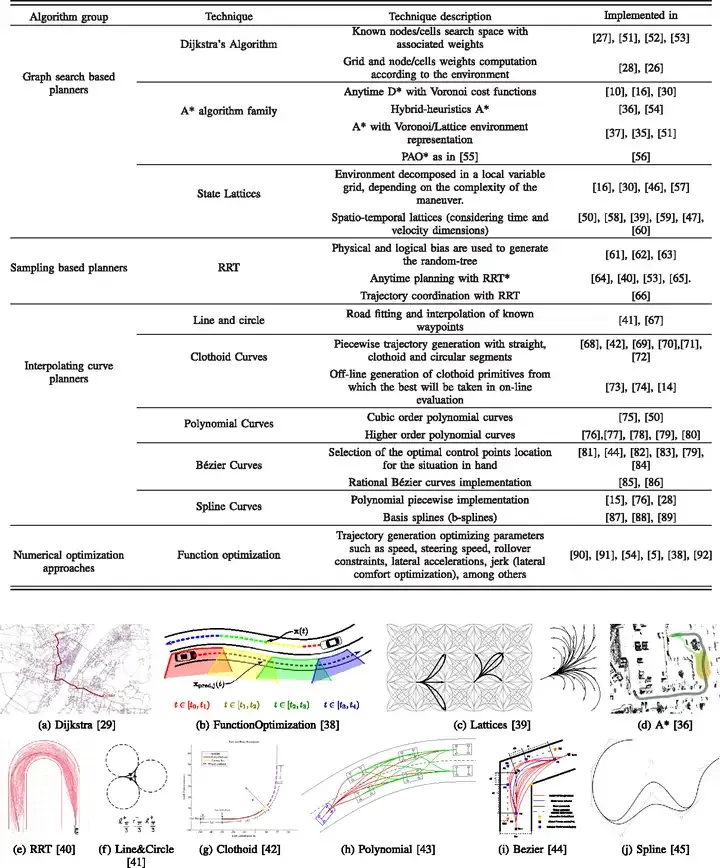
動作計画技術のアルゴリズムのおさらい

3.1.1 基本アルゴリズムPRMとRRT

(1) PRM

PRMアルゴリズム(確率的ロードマップ)。 PRM は主に 2 つのステップで構成され、1 つは学習段階、もう 1 つはクエリ段階です。

最初のステップ、学習段階: 状態空間の安全領域内の n 点を均一かつランダムにサンプリングし、サンプルが障害物に当たる点を削除します。その後、隣接する点を接続して衝突検出を実行し、障害物を排除します。 -衝突なしの接続、そして最終的に接続されたグラフを取得します。

2 番目のステップ、クエリ ステージ: 初期状態とターゲット状態の特定のペアに対して、前のステップで構築されたサンプリング ノードと連続性を使用し、グラフ検索メソッド (ダイクストラまたは A*) を使用して実現可能なパスを見つけます。

PRM の構築が完了すると、さまざまな初期状態と目標状態での動作計画の問題を解決するために使用できますが、この機能は無人車両の動作計画には不要です。さらに、PRM では状態間の正確な接続が必要ですが、これは複雑な微分制約を伴う動作計画の問題では非常に困難です。

(2) RRT

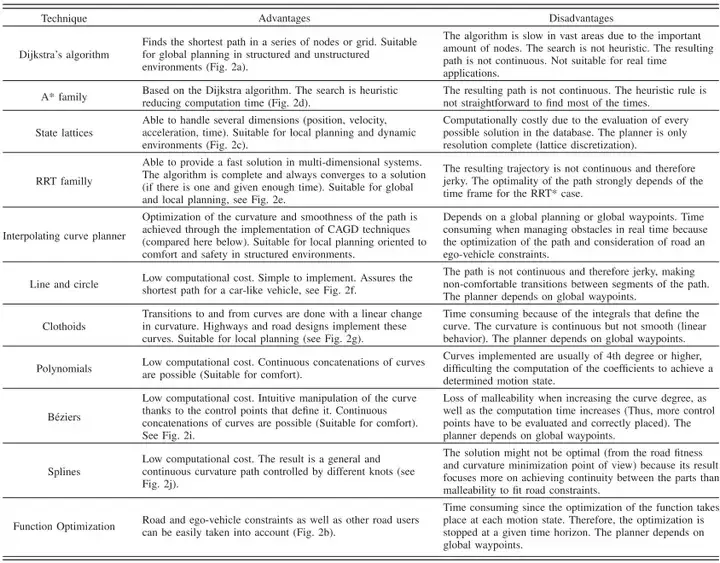
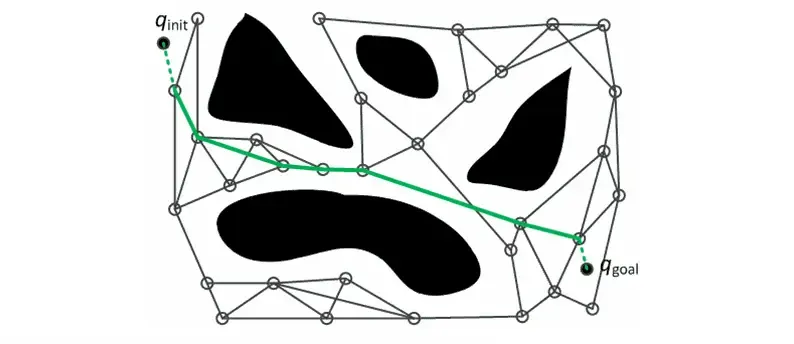
RRT (Rapidly-exploring Random Tree) アルゴリズム。 RRT は実際には、

ランダムにツリーを成長させる

という考えに基づいた一連のアルゴリズムを表しており、現在ロボット工学の分野で最も多くの最適化バリアントが使用されているアルゴリズムです。

① ツリーの初期化:ツリーのノード セットとエッジ セット。ノード セットには初期状態のみが含まれ、エッジ セットは空です。

② ツリーの成長: 状態空間をランダムにサンプリングします。サンプリング点が状態空間の安全領域にある場合、現在のツリー内のサンプリング点に最も近いノードを選択し、生成された場合はサンプリング点まで拡張します。軌跡が障害物と繋がっていない 物体が衝突すると、軌跡が木のエッジセットに追加され、軌跡の終点が木のノードセットに追加されます

③ 展開されるまで②を繰り返しますPRM の無向グラフと比較すると、RRT では、初期状態をルート ノード、ターゲット状態をリーフ ノードとするツリー構造が構築されます。初期状態とターゲット状態が異なると、異なるツリーが必要になります。構築される。

RRT は状態間の正確な接続を必要とせず、無人車両の動作計画などの動作ダイナミクス問題を解決するのにより適しています。

3.1.2 サンプリング法の問題点と解決策

解決効率と最適解かどうか。 PRM と RRT が確率的完全性を持つ理由は、それらが構成空間内のほぼすべての位置を横断するためです。

(1) 解決効率

解決効率の向上に関して、RRT 最適化の中心となる考え方は、ツリーをオープンエリアに誘導すること、つまり、ツリーをオープンエリアに近づけないようにすることです。障害物を回避し、障害物にあるノードを繰り返し確認することを避けることで効率が向上します。主な解決策:

① 均一サンプリング

標準的な RRT アルゴリズムは、状態空間を均一かつランダムにサンプリングします 現在のツリー内のノードが拡張を得る確率は、そのボロノイ領域面積に比例します。ツリーは状態に向かって移動します。空間の空の領域が成長し、状態空間の空き領域を均一に満たします。

RRT 接続アルゴリズムは、それぞれ initialstate と targetstate から始まる 2 つのツリーを同時に構築し、2 つのツリーが 一緒に成長するとき、実現可能な解決策が見つかります。 Go-biaing は、ターゲット状態をランダム サンプリング シーケンスに一定の割合で挿入し、ツリーをターゲット状態に向かって拡張するように導き、解を高速化し、解の品質を向上させます。

ヒューリスティック RRT は、ヒューリスティック関数を使用して、拡張コストの低いノードをサンプリングする確率を高め、ツリー内の各ノードのコストを計算します。ただし、複雑な環境では、この問題を解決するためのコスト関数の定義が困難です。 f -biased サンプリング手法では、まず状態空間をグリッドに離散化し、次にダイクストラ アルゴリズムを使用して各グリッドのコストを計算します。グリッドの領域内の点のコスト値はこの値に等しくなります。 、それによってヒューリスティック関数を構築します。

② 最適化された距離メトリック

距離は、2 つの構成間のパスのコストを測定するために使用され、ヒューリスティックなコスト関数の生成を支援し、ツリーの方向をガイドします。ただし、障害物を考慮すると距離の計算が難しくなります。運動計画における距離の定義はユークリッド距離に近い定義が採用されています。 RG-RRT (rechability guided RRT) は、サンプリング ポイントからノードまでの距離が到達可能なノードのセットよりも長い場合、RRT の探索能力に対する不正確な距離の影響を排除できます。ノード、距離、ノードを展開用に選択できます。

③ 衝突チェックの数を減らす

衝突チェックのサンプリング方法の効率のボトルネックの 1 つは、通常のアプローチではパスを等距離で離散化し、それぞれの構成に対して衝突チェックを実行することです。ポイント。解決完了 RRT は、障害物に近い ノード を削減することで拡張確率を取得し、特定の入力に対応する軌道が障害物と衝突した場合に、入力空間を 1 回だけ使用します。ペナルティ値がノードに追加されると、ノードが拡張される可能性が低くなります。ダイナミック ドメイン RRT とアダプティブ ダイナミック ドメイン RRT は、障害物に近いノードによる繰り返しの拡張失敗を防ぎ、アルゴリズムの効率を向上させるために、サンプリング領域を現在のツリーが配置されているローカル空間に制限します。

④ リアルタイムパフォーマンスの向上

いつでも、RRT は最初に RRT を迅速に構築し、実現可能なソリューションを取得してそのコストを記録し、その後サンプリングを継続しますが、実現可能なソリューションのコスト削減に有益なノードのみを RRT に挿入します。ツリーを作成し、それによって徐々により適切な実行可能なソリューションを取得します。再計画では、計画タスク全体を多数の等しい時間のサブタスク シーケンスに分解し、現在のタスクを実行しながら次のタスクを計画します。

(2) 最適性問題を解決するには、主に次の方法があります:

RGGアルゴリズム (ランダム幾何グラフ): ランダム幾何グラフ理論に基づいて、標準のPRMおよびRRTを改良した、漸近的な最適特性を持つPRM . RRG および RRT アルゴリズムは、状態空間内の n 点をランダムにサンプリングし、距離が r(n) 未満の点を接続して RGG を形成します。

RRT* アルゴリズム: RRG に基づく「再接続」ステップを導入して、隣接ポイントの親ノードとして新しく挿入されたノードがその隣接ポイントのコストを削減するかどうかを確認します。削減する場合は、元の親と子を削除します。現在の挿入ポイントを親ノードとする隣接ポイントの関係。これは RRT* アルゴリズムです。

LBT-RRT アルゴリズム: 多数のノード接続とローカル調整により、PRM と RRT は非常に非効率になります。 LBT-RRT アルゴリズムは、RRG アルゴリズムと RRT* アルゴリズムを組み合わせて、漸近的な最適性を得るという前提でより高い効率を実現します。

3.2 検索ベースのアルゴリズム

基本的な考え方は、状態空間を特定の方法でグラフに離散化し、その後、さまざまなヒューリスティック検索アルゴリズムを使用して実現可能な解決策、さらには最適な解決策を検索することです。ソリューション では、このカテゴリのアルゴリズムは比較的成熟しています。

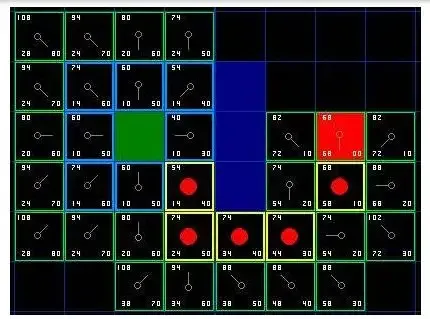
探索ベースのアルゴリズムの基礎は状態格子です。状態格子は状態空間の離散化であり、そのノードから始まり隣接するノードに到達するモーション プリミティブで構成されます。状態ノードは、そのモーション プリミティブ変換を別の状態ノードに渡すことができます。状態ラティスは、元の連続状態空間を検索グラフに変換します。動作計画の問題は、グラフ内の初期状態をターゲット状態に変換する一連の動作プリミティブを検索することになります。状態ラティスを構築した後、グラフ検索を使用できます。最適な軌道を探索するアルゴリズム。

3.2.1 基本アルゴリズムの構築 Dijkstra と A*

Dijkstra アルゴリズムは、構成空間全体を横断し、各 2 つのグリッド間の距離を見つけ、最終的に開始点から目標点までの最短経路とその幅を選択します。まず、このアルゴリズムにヒューリスティック関数、つまり検索されたノードから目的のノードまでの距離を追加し、これに基づいて再検索することで、グローバル検索による非効率を回避できます。 , 以下の図に示すように、赤色が検索エリアです。

図 6: A* アルゴリズムとダイクストラ アルゴリズムの効果の比較

3.2.2 検索方法の問題点と提案

サンプリングベースのアルゴリズムと同様に、このタイプのアルゴリズムも効率的かつ効率的である必要があります。最適な性的最適化。

効率の向上という点では、A* 自体は静的計画アルゴリズムであり、A* アルゴリズムの拡張である重み付き A* は、検索の重みを増やすことによってターゲット ノードへの検索方向をさらに導きます。速度は非常に速いですが、極小値に陥りやすく、大域的な最適解を保証できません。

移動車両の場合、A* の微分アルゴリズム D (動的 A) を使用すると、効率が大幅に向上します。 LPA も動的計画に基づいており、このアルゴリズムは、状態グリッドのモーション プリミティブのコストが時間とともに変化する状況に対処でき、より少ない数のモーション プリミティブを再探索することで新しい最適なプランを計画できます。ノード。 LPA

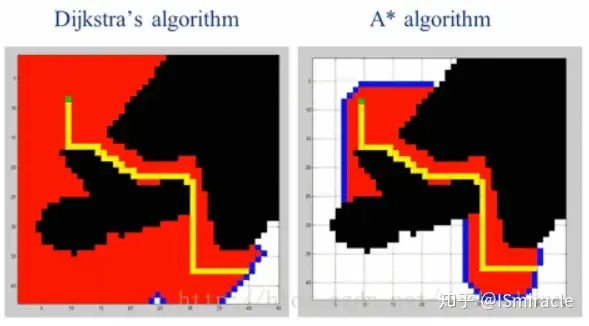
に基づいて開発されたD*-Liteは、D*と同じ結果をより高い効率で達成できます。

最適なソリューションを検索する場合、ARA* は重み付け A* に基づいて開発されたいつでも検索アルゴリズムであり、重み付け A* アルゴリズムを複数回呼び出し、呼び出しごとにヒューリスティック関数の重みを減らします。セット INCONS を導入することにより、各サイクルは前のサイクルの情報を引き続き使用してパスを最適化し、徐々に最適解に近づくことができます。

アルゴリズムの効率と最適性のバランスに関して、Sandin aine らは、複数のヒューリスティック関数を導入して、ヒューリスティック関数の 1 つが単独で使用された場合でも最適なソリューションを見つけられるようにする MHA* アルゴリズムを提案しました。さまざまなヒューリスティック関数によって生成されたアルゴリズムは、アルゴリズムの効率と最適性を考慮できます。 DMHA は、MHA に基づいて適切なヒューリスティック関数をオンラインかつリアルタイムで生成するため、ローカル ミニマム問題が回避されます。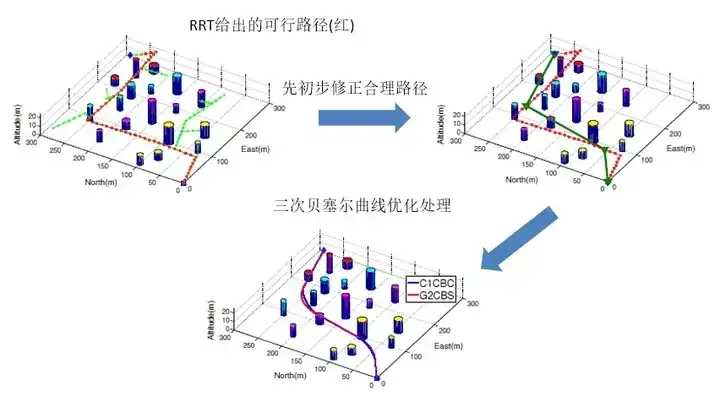

3.3 補間フィッティングに基づくアルゴリズム

補間フィッティングに基づくアルゴリズムは、次のように定義できます:

データ補間 と を使用して、ロードマップを記述するために使用される一連の既知の点セットに基づいてカーブフィッティング法は、スマートカーが走行する経路を作成し、より優れた連続性とより高い微分可能性を提供します。具体的な方法は以下の通りです: Dubins 曲線と Reeds and Sheep (RS) 曲線は、配置空間内の任意の 2 点を結ぶ最短経路であり、それぞれ反転なしと反転ありの状況に対応します。これらはすべて円弧と最大曲率の直線で構成されており、円弧と直線の接続部分には曲率の不連続部があり、実際の車両がこのような曲線を走行する場合には、その不連続部で停止してステアリングホイールを調整する必要があります。運転を続けるための曲率。

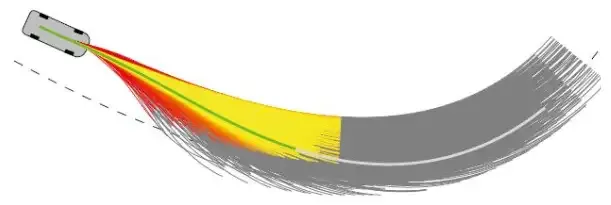
多項式補間曲線

は、ノードの要件を満たすことで多項式係数を設定でき、縦方向の制約制御には 4 次多項式がよく使用され、5 次多項式がよく使用されます。多項式は縦方向の拘束制御に使用されることが多く、3次多項式は追い越し軌道にも使用されます。

スプライン曲線は閉じた表現を持ち、曲率の連続性を容易に確保できます。 βスプライン曲線は曲率の連続性を実現でき、3次ベジェ曲線は曲率の連続性と有界性を確保でき、計算量も比較的少ない。 η^3 曲線 [43] は 7 次のスプライン曲線で、曲率の連続性と曲率導関数の連続性という非常に優れた特性を持ち、高速車両にとって非常に意味があります。

3.4 最適制御に基づくアルゴリズム

最適制御に基づくアルゴリズムは、主に MPC が障害物を回避するためのローカルな経路計画を実行できるため、経路計画に分類されます。また、MPC の主な機能は軌道を追跡することです。必要な力学と運動学的制約に加えて、考慮される問題には、快適性、感覚情報の不確実性、将来の車両間通信の不確実性も考慮する必要があり、ローカル軌道を計画する際には、ドライバーも制御ループに含めることができます。前述の不確実性の問題とドライバーの制御ループへの組み込みについては、セクション 4 で説明します。 MPC の研究は主に、最適化理論とエンジニアリングの実践という 2 つの側面から始まります。前者については、Dimitri P. Bertsekas 著『Convex Optimization Algorithms』と James B. Rawlings 著『Model Predictive Control: Theory, Computation, and Design』をお勧めします。中国語分野では、Liu Haoyang 先生の最適化本が比較的明確で理解しやすいと個人的に感じています。後者については、まず Gong Jianwei 先生の自動運転 MPC の本を強くお勧めします。本の古いバージョンではデモに問題がありましたが、新しいバージョンではすべて解決されました。

MPC で使用される予測モデルは、畳み込みニューラル ネットワーク、ファジー制御、状態空間など、数多くあります。その中で、最も一般的に使用されるのは状態空間法です。 MPC は次のように簡単に表現できます。必要な力学、運動学などの制約が満たされると、数値的手段を通じてモデルの最適解が解かれます。最適解は、ステアリング ホイール角度などの状態方程式の制御変数です。 、などの制御量を車両モデルに適用して、速度、加速度、座標などの必要な状態量を取得します。

上記の説明から、MPC の鍵はモデルの構築と解決にあり、モデルの構築をいかに等価的に簡素化し、解決の効率を向上させるかが最優先事項であることがわかります。車両は異なる制御入力の下で異なる軌道をとり、それぞれの軌道は目的関数値に対応します。無人車両は解決アルゴリズムを使用して最小の目的関数値に対応する制御量を見つけ、それを上記の車両に適用します。 、以下の図に示すように:

モデリングの難しさを軽減するために、人工の位置エネルギー場のモデルもモデリングに使用されます。人工の位置エネルギー場の基本的な考え方は電場と似ています。道路上の障害物は、異なる電荷極性を持つ電界の電界源に似ています。障害物 (動的、静的) における位置エネルギーはより高く、無人車両は位置エネルギーの低い位置に向かって移動します。

4 オープンソース プロジェクト

オープンソース プロジェクトを推奨します CppRobotics:

• 経路計画
• ディクストラ
• スター
• RRT
• ダイナミック ウィンドウ アプローチ
• モデル予測軌道ジェネレーター
• 3次スプラインプランナー
• 状態格子プランナー
• フレネフレーム軌道

5 学習方法

新しい分野を始めるための学習コンテキストは次のとおりです: エンジニアリング、理論、ビジョントロイカは連携してパス計画を立てます。例:

5.1エンジニアリング

は、幅から各アルゴリズムの内容を理解し、同時に深さから各アルゴリズムの詳細を学習しながら、各パス計画アルゴリズムの内容を理解することを指します。 。経路計画の分野のアルゴリズムに関しては、現時点では包括的なチュートリアルはありませんが、Gong Jianwei の NMPC 動作計画が参考になります。

5.2 理論

は、これらのアルゴリズムの動作をサポートする数学的原理と、これらのアルゴリズムが生成される理由 (数学的観点) を理解することを指します。

• 目的関数と制約を構築し、同時に極値を求めて最適な制御変数(経路)を求めることは、最適化理論に属します。
• 一般的なニュートン法、最急降下法などは、これらの数値解法の本質は、代数方程式を数値的に解くことに由来し、解法プロセスで見られる導関数ヤコビ行列、判定条件のベクトルノルムに属します。などは、本質的には 1 次元の数値解を変換するものであり、数値解は高次元に達し、
行列理論
• に属します。

5.3 ビジョン

は、科学研究文書や結果レポートなどを使用して、科学研究および企業におけるパス計画の主な用途を理解することを指します。

6 まとめ

この記事では、電流パス計画の概要を紹介し、電流パス計画方法を理解します。内容は非常に複雑で、実践的な応用指向がなければ、短期間ですべてを学ぶのは困難です。必要なときだけ集中して学ぶことができます。