Le modèle de diffusion ouvre une nouvelle ère de modèles génératifs avec ses excellentes performances en génération d'images. De grands modèles comme Stable Diffusion, DALLE, Imagen, SORA… ont vu le jour, enrichissant encore les perspectives d’application de l’IA générative. Cependant, les modèles de diffusion actuels ne sont pas théoriquement parfaits et peu d’études se sont intéressées au problème des singularités indéfinies aux extrémités du temps d’échantillonnage. De plus, le niveau de gris moyen causé par le problème de singularité dans l'application et d'autres problèmes affectant la qualité de l'image générée n'ont pas été résolus.
Afin de résoudre ce problème, l'équipe WeChat Vision a collaboré avec l'Université Sun Yat-sen pour explorer conjointement le problème de singularité dans le modèle de diffusion et a proposé une méthode plug-and-play qui a résolu efficacement le problème d'échantillonnage au niveau moment initial. Cette méthode résout avec succès le problème du niveau de gris moyen et améliore considérablement la capacité de génération des modèles de diffusion existants. Les résultats de la recherche ont été présentés lors de la conférence CVPR 2024.
Les modèles de diffusion ont obtenu un succès significatif dans les tâches de génération de contenu multimodal, notamment la génération d'images, d'audio, de texte et de vidéo. La modélisation réussie de ces modèles repose principalement sur l'hypothèse que le processus inverse du
processus de diffusion est également conforme aux propriétés gaussiennes. Cependant, cette hypothèse n'a pas été entièrement prouvée. Surtout au point final, c'est-à-dire t=0 ou t=1, le problème de singularité se produira, ce qui limite les méthodes existantes pour étudier l'échantillonnage au niveau de la singularité.
De plus, le problème de singularité affectera également la capacité de génération du modèle de diffusion, provoquant le
problème d'échelle de gris moyendu modèle, c'est-à-dire qu'il est difficile de générer des images avec une luminosité forte ou faible, car illustré dans la figure ci-dessous. Cela limite également dans une certaine mesure le champ d’application des modèles de diffusion actuels.
Afin de résoudre le problème de singularité du modèle de diffusion au point final temporel, l'équipe de vision WeChat a coopéré avec l'Université Sun Yat-sen pour mener des recherches approfondies sous les aspects théoriques et pratiques. Premièrement, l’équipe a proposé une limite supérieure d’erreur contenant une distribution gaussienne approximative du processus inverse au moment de singularité, ce qui a fourni une base théorique pour les recherches ultérieures. Sur la base de cette garantie théorique, l'équipe a étudié l'échantillonnage en points singuliers et est parvenue à deux conclusions importantes : 1) Le point singulier à t=1 peut être converti en un point singulier détachable en trouvant la limite, 2) La singularité à t=0 est une propriété inhérente au modèle de diffusion et ne doit pas être évitée. Sur la base de ces conclusions, l'équipe a proposé une méthode plug-and-play :
SingDiffusion, pour résoudre le problème de l'échantillonnage du modèle de diffusion au moment initial.
Un grand nombre de vérifications expérimentales ont montré que le module SingDiffusion peut être appliqué de manière transparente aux modèles de diffusion existants avec une seule formation, résolvant ainsi de manière significative le problème de la valeur de gris moyenne. Sans utiliser une technologie de guidage sans classificateur, SingDiffusion peut améliorer considérablement la qualité de génération des méthodes actuelles. Surtout après avoir été appliqué à Stable Diffusion1.5 (SD-1.5), la qualité des images générées est améliorée de 33 %.
Adresse de l'article : https://arxiv.org/pdf/2403.08381.pdf
 Adresse du projet : https://pangzecheung.github.io/SingDiffusion/
Titre de l'article : S'attaquer aux singularités aux extrémités des intervalles de temps en diffusion Modèles
Propriétés gaussiennes du processus inverse
Adresse du projet : https://pangzecheung.github.io/SingDiffusion/
Titre de l'article : S'attaquer aux singularités aux extrémités des intervalles de temps en diffusion Modèles
Propriétés gaussiennes du processus inverse
Afin d'étudier le problème de singularité du modèle de diffusion, il est nécessaire de vérifier que le processus inverse de l'ensemble du processus incluant la singularité satisfait le gaussien propriétés. Définissez d'abord
comme l'échantillon d'apprentissage du modèle de diffusion. La distribution de l'échantillon d'apprentissage peut être exprimée comme suit :
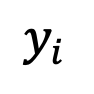 .
Où δ représente la fonction Dirac. Selon la définition du modèle de diffusion temporelle continue dans [1], pour deux instants 0≤s,t≤1, le processus direct peut être exprimé comme suit :
où
.
Où δ représente la fonction Dirac. Selon la définition du modèle de diffusion temporelle continue dans [1], pour deux instants 0≤s,t≤1, le processus direct peut être exprimé comme suit :
où
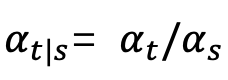 ,
,
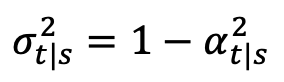 ,
,
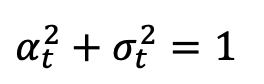 ,
,
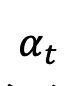 sont monotones avec temps Passage de 1 à 0. Compte tenu de la distribution de l'échantillon d'apprentissage que nous venons de définir, la densité de probabilité marginale à un instant donné de
sont monotones avec temps Passage de 1 à 0. Compte tenu de la distribution de l'échantillon d'apprentissage que nous venons de définir, la densité de probabilité marginale à un instant donné de
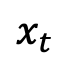 peut être exprimée comme suit :
peut être exprimée comme suit :
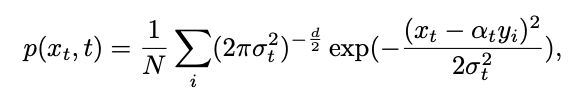
À partir de là, la distribution conditionnelle du processus inverse peut être calculée à l'aide de la formule de Bayes :
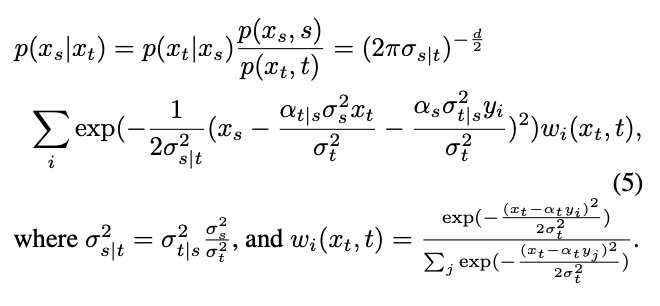
Cependant, la distribution est un mélange de distributions gaussiennes, difficile à intégrer dans un réseau. Par conséquent, les modèles de diffusion traditionnels supposent généralement que cette distribution peut être ajustée par une seule distribution gaussienne.
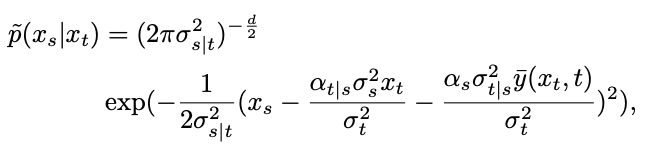
où,
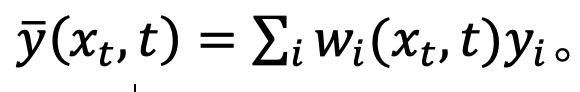 Pour tester cette hypothèse, l'étude estime l'erreur de cet ajustement dans la proposition 1.
Pour tester cette hypothèse, l'étude estime l'erreur de cet ajustement dans la proposition 1.
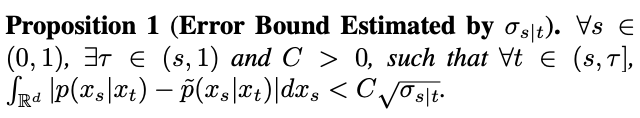
Cependant, l'étude a révélé que lorsque t = 1, lorsque s s'approche de 1,
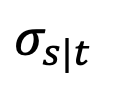 s'approche également de 1, et l'erreur ne peut être ignorée. Par conséquent, la proposition 1 ne prouve pas la propriété gaussienne inverse à t=1. Afin de résoudre ce problème, cette étude donne une nouvelle proposition :
s'approche également de 1, et l'erreur ne peut être ignorée. Par conséquent, la proposition 1 ne prouve pas la propriété gaussienne inverse à t=1. Afin de résoudre ce problème, cette étude donne une nouvelle proposition :
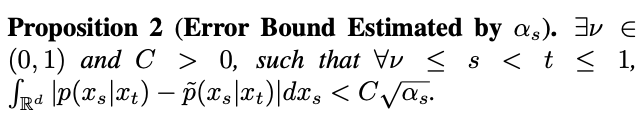
Selon la proposition 2, lorsque t=1, lorsque s tend vers 1,
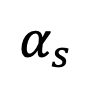 tendra vers 0. Ainsi, cette étude prouve que l’ensemble du processus inverse, y compris le moment de singularité, est conforme aux caractéristiques gaussiennes.
Échantillonnage au moment de singularité
Avec la garantie des caractéristiques gaussiennes du processus inverse, cette étude a mené une étude sur l'échantillonnage au moment de singularité basée sur la formule d'échantillonnage inverse.
Considérons d'abord le problème de singularité au temps t=1. Lorsque t=1,
tendra vers 0. Ainsi, cette étude prouve que l’ensemble du processus inverse, y compris le moment de singularité, est conforme aux caractéristiques gaussiennes.
Échantillonnage au moment de singularité
Avec la garantie des caractéristiques gaussiennes du processus inverse, cette étude a mené une étude sur l'échantillonnage au moment de singularité basée sur la formule d'échantillonnage inverse.
Considérons d'abord le problème de singularité au temps t=1. Lorsque t=1,
 =0, la formule d'échantillonnage suivante aura le dénominateur divisé par 0 :
=0, la formule d'échantillonnage suivante aura le dénominateur divisé par 0 :
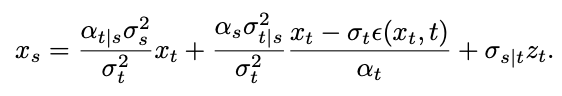
L'équipe de recherche a découvert qu'en calculant la limite, le point singulier peut être transformé en un point singulier détachable :
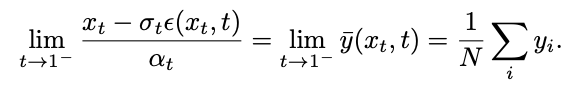
Cependant, cette limite ne peut pas être calculée lors des tests. À cette fin, cette étude propose que nous puissions ajuster
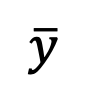 au temps t=1 et utiliser la « prédiction x » pour résoudre le problème d'échantillonnage au point singulier initial.
Considérons ensuite le temps t=0, le processus inverse d'ajustement de la distribution gaussienne deviendra une distribution gaussienne de variance 0, c'est-à-dire la fonction Dirac :
au temps t=1 et utiliser la « prédiction x » pour résoudre le problème d'échantillonnage au point singulier initial.
Considérons ensuite le temps t=0, le processus inverse d'ajustement de la distribution gaussienne deviendra une distribution gaussienne de variance 0, c'est-à-dire la fonction Dirac :
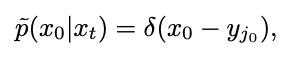
où
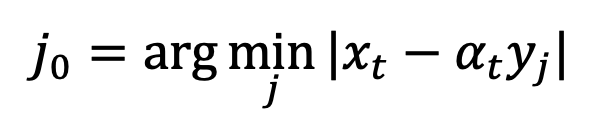 . De telles singularités feront converger le processus d'échantillonnage vers les données correctes
. De telles singularités feront converger le processus d'échantillonnage vers les données correctes
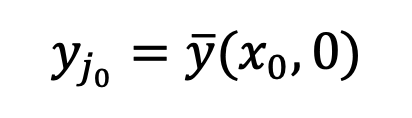 . Par conséquent, la singularité à t=0 est une bonne propriété du modèle de diffusion et ne doit pas être évitée.
De plus, l'étude explore également le problème de singularité dans DDIM, SDE, ODE en annexe.
Module SingDiffusion Plug-and-play
L'échantillonnage à des points singuliers affectera la qualité de l'image générée par le modèle de diffusion. Par exemple, lors de la saisie d'indices de luminosité élevée ou faible, les méthodes existantes ne peuvent souvent générer que des images avec une échelle de gris moyenne, ce que l'on appelle le problème de l'échelle de gris moyenne. Ce problème vient du fait que les méthodes existantes ignorent l'échantillonnage au point singulier à t = 0 et utilisent à la place la
distribution gaussienne standardcomme distribution initiale pour l'échantillonnage au temps 1-ϵ. Cependant, comme le montre la figure ci-dessus, il existe un écart important entre la distribution gaussienne standard et la distribution réelle des données au temps 1-ϵ.
. Par conséquent, la singularité à t=0 est une bonne propriété du modèle de diffusion et ne doit pas être évitée.
De plus, l'étude explore également le problème de singularité dans DDIM, SDE, ODE en annexe.
Module SingDiffusion Plug-and-play
L'échantillonnage à des points singuliers affectera la qualité de l'image générée par le modèle de diffusion. Par exemple, lors de la saisie d'indices de luminosité élevée ou faible, les méthodes existantes ne peuvent souvent générer que des images avec une échelle de gris moyenne, ce que l'on appelle le problème de l'échelle de gris moyenne. Ce problème vient du fait que les méthodes existantes ignorent l'échantillonnage au point singulier à t = 0 et utilisent à la place la
distribution gaussienne standardcomme distribution initiale pour l'échantillonnage au temps 1-ϵ. Cependant, comme le montre la figure ci-dessus, il existe un écart important entre la distribution gaussienne standard et la distribution réelle des données au temps 1-ϵ.
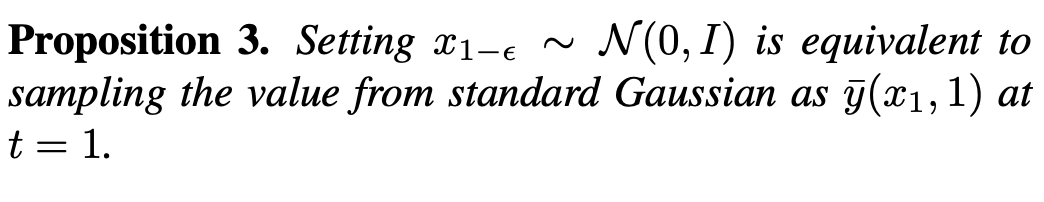
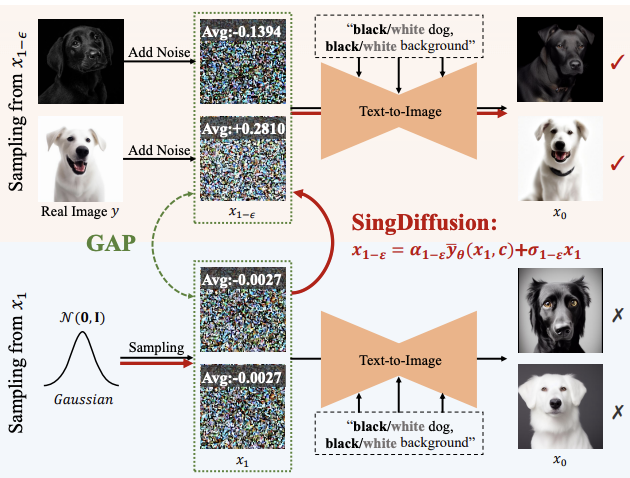
Sous un tel écart, selon la proposition 3, la méthode existante équivaut à générer une image avec une valeur moyenne de 0 à t=1, c'est-à-dire une image moyenne en niveaux de gris. Par conséquent, il est difficile pour les méthodes existantes de générer des images avec une luminosité extrêmement forte ou faible. Pour résoudre ce problème, cette étude propose une méthode SingDiffusion plug-and-play pour combler cet écart en ajustant la conversion entre une distribution gaussienne standard et la distribution réelle des données. L'algorithme de
SingDiffuion est présenté dans la figure ci-dessous :

D'après la conclusion de la section précédente, cette étude a utilisé la méthode "x - prédiction" à t=1 pour résoudre le problème d'échantillonnage à le point singulier. Pour les paires de données image-texte
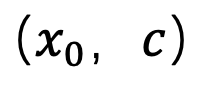 , cette méthode entraîne un Unet
, cette méthode entraîne un Unet
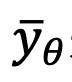 à s'adapter
à s'adapter
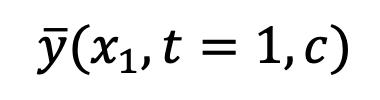 . La fonction de perte est exprimée comme suit :
. La fonction de perte est exprimée comme suit :
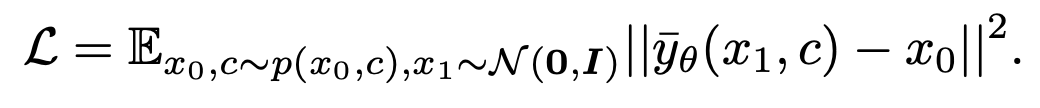
Une fois le modèle convergé, vous pouvez suivre la formule d'échantillonnage DDIM ci-dessous et utiliser le module
 sampling
sampling
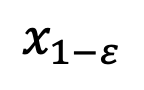 nouvellement obtenu.
nouvellement obtenu.
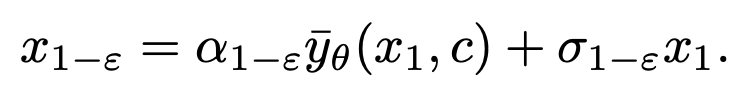
La formule d'échantillonnage de
DDIM garantit que le
 généré est conforme à la distribution des données
généré est conforme à la distribution des données
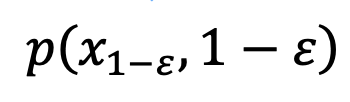 au moment 1-ε, résolvant ainsi le problème des niveaux de gris moyens. Après cette étape, le modèle pré-entraîné peut être utilisé pour effectuer les étapes d'échantillonnage suivantes jusqu'à ce que
au moment 1-ε, résolvant ainsi le problème des niveaux de gris moyens. Après cette étape, le modèle pré-entraîné peut être utilisé pour effectuer les étapes d'échantillonnage suivantes jusqu'à ce que
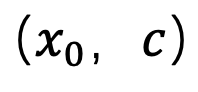 soit généré. Il convient de noter que puisque cette méthode ne participe qu’à la première étape de l’échantillonnage et n’a rien à voir avec le processus d’échantillonnage ultérieur, SingDiffusion peut être appliquée à la plupart des modèles de diffusion existants. De plus, afin d'éviter le problème de débordement de données provoqué par l'opération sans guidage du classificateur, cette méthode utilise également l'opération de normalisation suivante :
soit généré. Il convient de noter que puisque cette méthode ne participe qu’à la première étape de l’échantillonnage et n’a rien à voir avec le processus d’échantillonnage ultérieur, SingDiffusion peut être appliquée à la plupart des modèles de diffusion existants. De plus, afin d'éviter le problème de débordement de données provoqué par l'opération sans guidage du classificateur, cette méthode utilise également l'opération de normalisation suivante :
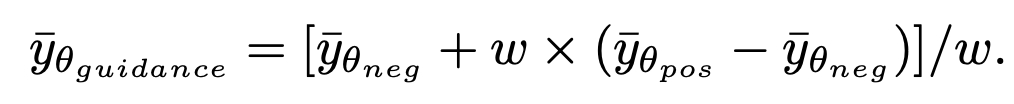
où guidage représente le résultat après l'opération sans guidage du classificateur, et neg représente le résultat sous les invites négatives Sortie, pos représente la sortie sous les invites positives et ω représente la force du guidage.
Tout d'abord, cette étude a vérifié la capacité de SingDiffusion à résoudre le problème moyen des niveaux de gris sur trois modèles : SD-1.5, SD-2.0-base et SD-2.0. Cette étude a sélectionné quatre invites extrêmes, notamment « fond blanc/noir pur » et « logo de dessin au trait monochrome sur fond blanc/noir », comme conditions de génération, et a calculé la valeur moyenne en niveaux de gris de l'image générée, comme indiqué dans le tableau ci-dessous. Montré :
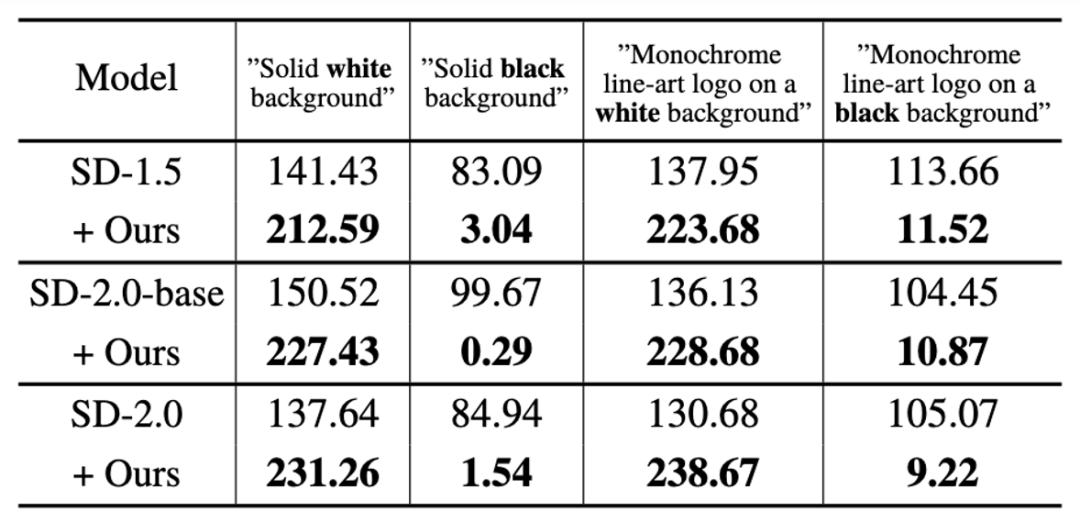
Comme le montre le tableau, cette recherche peut résoudre de manière significative le problème de la valeur de gris moyenne et générer des images qui correspondent à la luminosité de la description du texte saisi. De plus, l'étude a également visualisé les résultats de génération sous ces quatre instructions d'invite, comme le montre la figure ci-dessous :

Comme le montre la figure, après avoir ajouté cette méthode, le modèle de diffusion existant peut générer du noir ou du blanc. image.
Pour étudier plus en détail l'amélioration de la qualité de l'image obtenue par cette méthode, l'étude a sélectionné 30 000 descriptions à tester sur l'ensemble de données COCO. Tout d'abord, cette étude démontre la capacité générative du modèle lui-même sans utiliser de guidage sans classificateur, comme le montre le tableau suivant :

Comme le montre le tableau, la méthode proposée peut réduire considérablement le FID de les images générées et améliorer les indicateurs CLIP. Il convient de noter que dans le modèle SD-1.5, la méthode présentée dans cet article réduit l'indice FID de 33 % par rapport au modèle original.
De plus, afin de vérifier la capacité de génération de la méthode proposée sans guidage du classificateur, l'étude montre également dans la figure ci-dessous que sous différentes tailles de guidage ω∈[1.5,2,3,4,5,6, 7,8] Courbe de Pareto de CLIP vs FID :
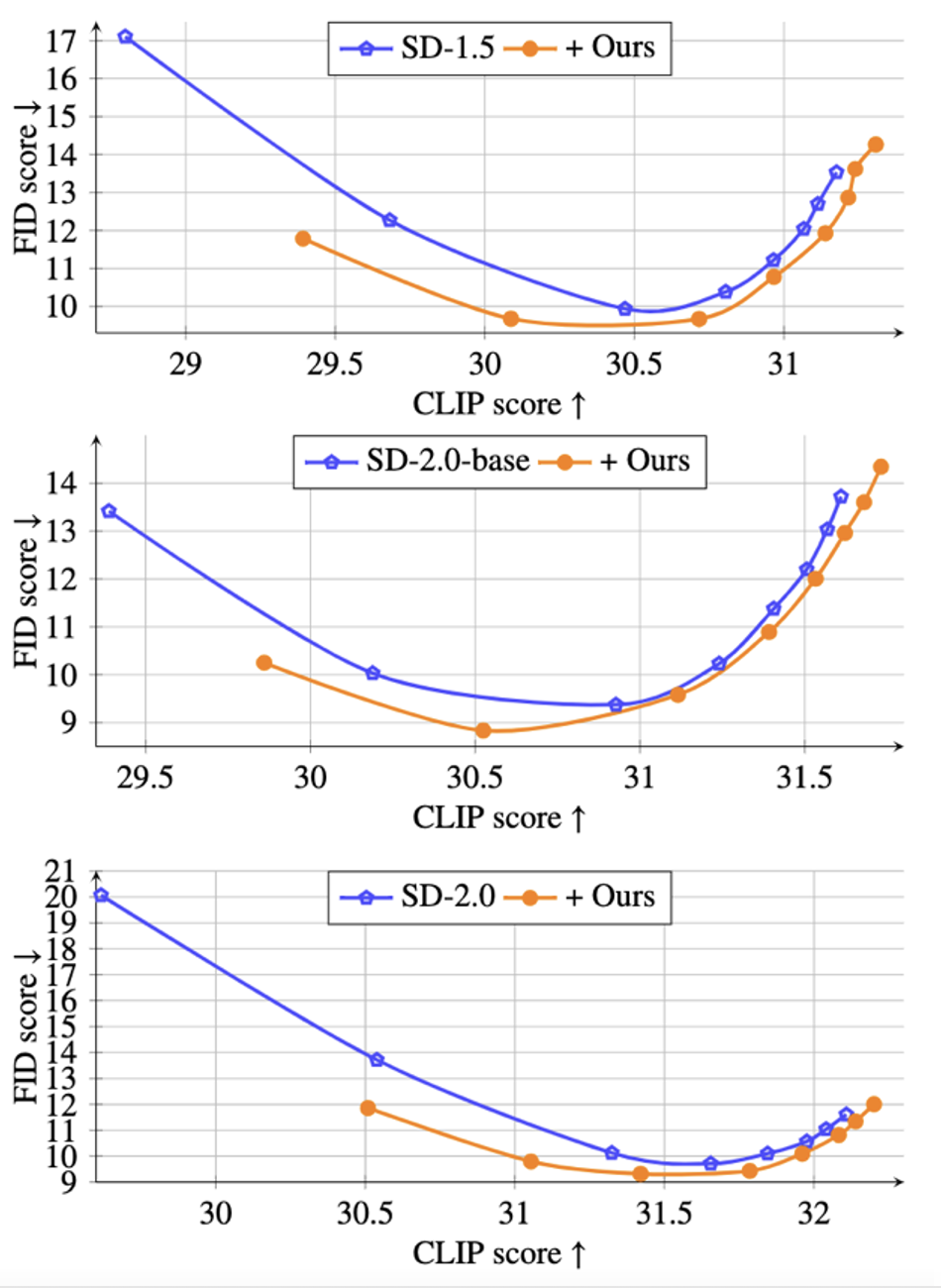
Comme le montre la figure, au même niveau CLIP, la méthode proposée peut obtenir des valeurs FID inférieures et générer des images plus réalistes.
De plus, cette étude démontre également la capacité de généralisation de la méthode proposée sous différents modèles pré-entraînés CIVITAI, comme le montre la figure ci-dessous :

On peut voir que la méthode proposée dans cette étude il suffit d'après une formation, il peut être facilement appliqué aux modèles de diffusion existants pour résoudre le problème du niveau de gris moyen.
Enfin, la méthode proposée par cette recherche peut également être appliquée de manière transparente au modèle ControlNet pré-entraîné, comme le montre la figure ci-dessous :

Comme le montrent les résultats, cette méthode peut résoudre efficacement la moyenne problème gris du problème du degré ControlNet.
[1] Tero Karras, Miika Aittala, Timo Aila et Samuli Laine, pages. 26565-26577, 2022. 3
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

 Adresse du projet : https://pangzecheung.github.io/SingDiffusion/
Adresse du projet : https://pangzecheung.github.io/SingDiffusion/
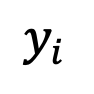 .
.
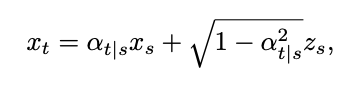
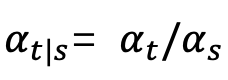 ,
,
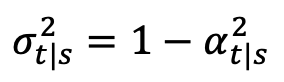 ,
,
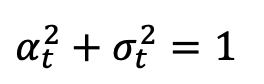 ,
,
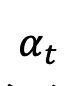 sont monotones avec temps Passage de 1 à 0. Compte tenu de la distribution de l'échantillon d'apprentissage que nous venons de définir, la densité de probabilité marginale à un instant donné de
sont monotones avec temps Passage de 1 à 0. Compte tenu de la distribution de l'échantillon d'apprentissage que nous venons de définir, la densité de probabilité marginale à un instant donné de
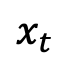 peut être exprimée comme suit :
peut être exprimée comme suit :
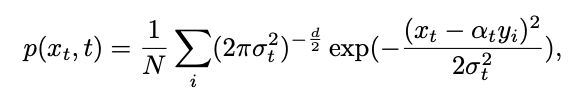
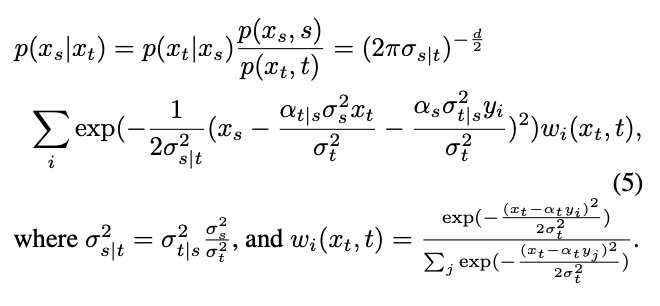
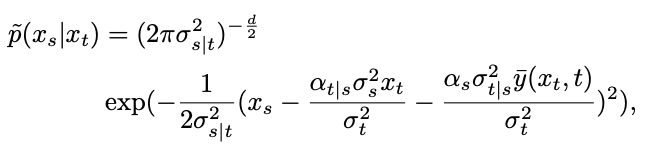
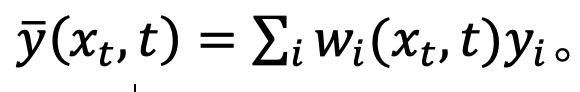 Pour tester cette hypothèse, l'étude estime l'erreur de cet ajustement dans la proposition 1.
Pour tester cette hypothèse, l'étude estime l'erreur de cet ajustement dans la proposition 1.
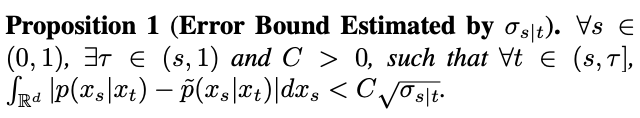
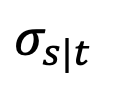 s'approche également de 1, et l'erreur ne peut être ignorée. Par conséquent, la proposition 1 ne prouve pas la propriété gaussienne inverse à t=1. Afin de résoudre ce problème, cette étude donne une nouvelle proposition :
s'approche également de 1, et l'erreur ne peut être ignorée. Par conséquent, la proposition 1 ne prouve pas la propriété gaussienne inverse à t=1. Afin de résoudre ce problème, cette étude donne une nouvelle proposition :
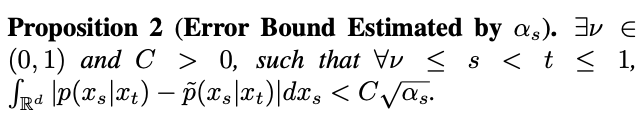
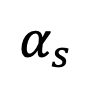 tendra vers 0. Ainsi, cette étude prouve que l’ensemble du processus inverse, y compris le moment de singularité, est conforme aux caractéristiques gaussiennes.
tendra vers 0. Ainsi, cette étude prouve que l’ensemble du processus inverse, y compris le moment de singularité, est conforme aux caractéristiques gaussiennes.
 =0, la formule d'échantillonnage suivante aura le dénominateur divisé par 0 :
=0, la formule d'échantillonnage suivante aura le dénominateur divisé par 0 :
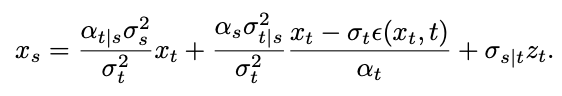
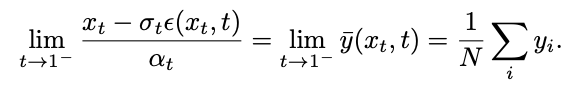
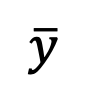 au temps t=1 et utiliser la « prédiction x » pour résoudre le problème d'échantillonnage au point singulier initial.
au temps t=1 et utiliser la « prédiction x » pour résoudre le problème d'échantillonnage au point singulier initial.
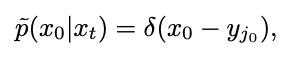
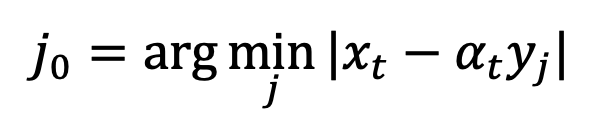 . De telles singularités feront converger le processus d'échantillonnage vers les données correctes
. De telles singularités feront converger le processus d'échantillonnage vers les données correctes
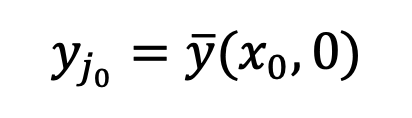 . Par conséquent, la singularité à t=0 est une bonne propriété du modèle de diffusion et ne doit pas être évitée.
. Par conséquent, la singularité à t=0 est une bonne propriété du modèle de diffusion et ne doit pas être évitée.
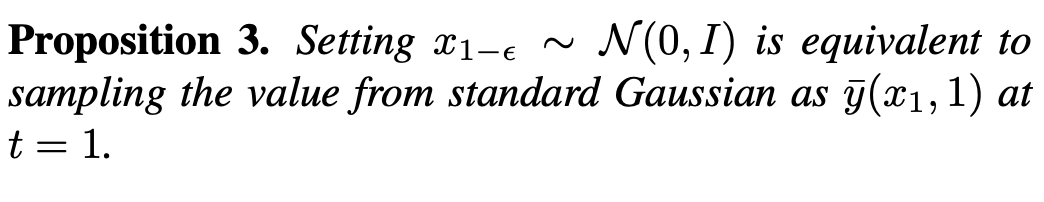

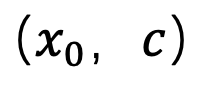 , cette méthode entraîne un Unet
, cette méthode entraîne un Unet
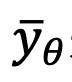 à s'adapter
à s'adapter
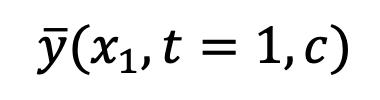 . La fonction de perte est exprimée comme suit :
. La fonction de perte est exprimée comme suit :
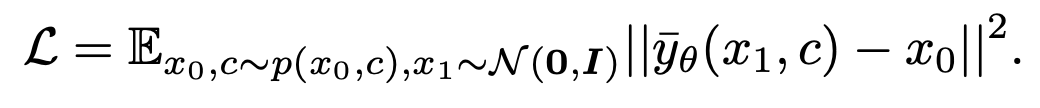
 sampling
sampling
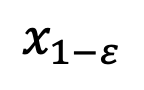 nouvellement obtenu.
nouvellement obtenu.
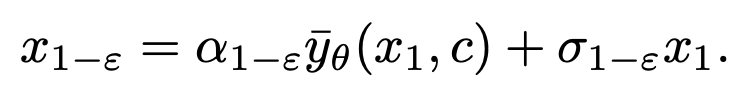
 généré est conforme à la distribution des données
généré est conforme à la distribution des données
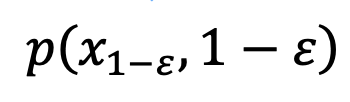 au moment 1-ε, résolvant ainsi le problème des niveaux de gris moyens. Après cette étape, le modèle pré-entraîné peut être utilisé pour effectuer les étapes d'échantillonnage suivantes jusqu'à ce que
au moment 1-ε, résolvant ainsi le problème des niveaux de gris moyens. Après cette étape, le modèle pré-entraîné peut être utilisé pour effectuer les étapes d'échantillonnage suivantes jusqu'à ce que
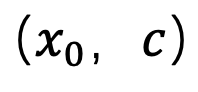 soit généré. Il convient de noter que puisque cette méthode ne participe qu’à la première étape de l’échantillonnage et n’a rien à voir avec le processus d’échantillonnage ultérieur, SingDiffusion peut être appliquée à la plupart des modèles de diffusion existants. De plus, afin d'éviter le problème de débordement de données provoqué par l'opération sans guidage du classificateur, cette méthode utilise également l'opération de normalisation suivante :
soit généré. Il convient de noter que puisque cette méthode ne participe qu’à la première étape de l’échantillonnage et n’a rien à voir avec le processus d’échantillonnage ultérieur, SingDiffusion peut être appliquée à la plupart des modèles de diffusion existants. De plus, afin d'éviter le problème de débordement de données provoqué par l'opération sans guidage du classificateur, cette méthode utilise également l'opération de normalisation suivante :
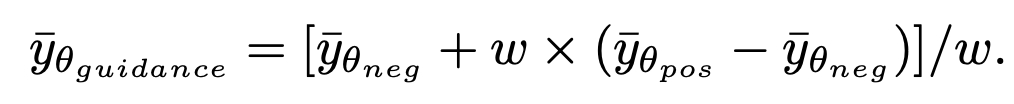






 js actualiser la page actuelle
js actualiser la page actuelle Comment gagner de l'argent avec la blockchain
Comment gagner de l'argent avec la blockchain Utilisation du framework DWZ
Utilisation du framework DWZ Comment configurer l'hibernation dans le système Win7
Comment configurer l'hibernation dans le système Win7 Ouvrir le dossier personnel sur Mac
Ouvrir le dossier personnel sur Mac Savez-vous si vous annulez l'autre personne immédiatement après l'avoir suivie sur Douyin ?
Savez-vous si vous annulez l'autre personne immédiatement après l'avoir suivie sur Douyin ? Que signifie formater un téléphone mobile ?
Que signifie formater un téléphone mobile ? arithmétique binaire
arithmétique binaire