
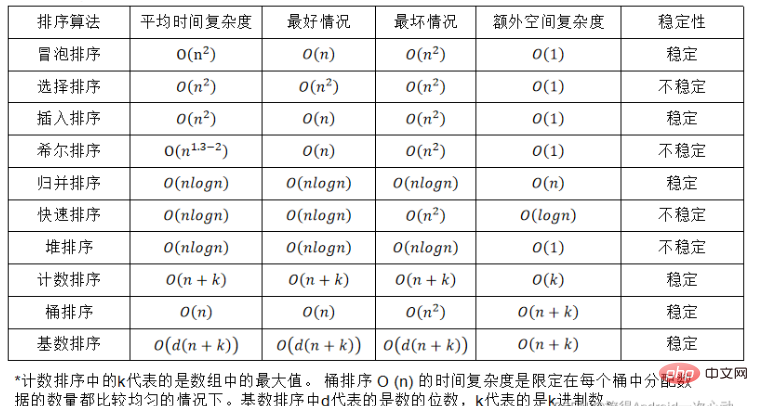
On suppose qu'il y a plusieurs enregistrements avec les mêmes mots-clés dans la séquence d'enregistrements à trier. Si après le tri, il est garanti que l'ordre relatif de ces enregistrements reste inchangé, cela. est, dans la séquence originale, a[i]=a[j], et a[i] est avant a[j], et si a[i] est toujours avant a[j] après le tri, on dit que ceci l'algorithme de tri est stable ; sinon, il est appelé instabilité.
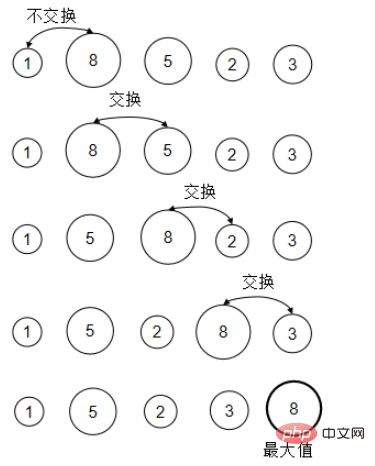
Sélectionnez à chaque fois le plus petit élément parmi les éléments à trier, et échangez-le avec les éléments en 1ère, 2ème, 3ème... position tour à tour. Cela forme une zone ordonnée à l’avant du réseau. Chaque fois qu'un échange est effectué, la longueur de la région ordonnée est augmentée de un.
public static void selectionSort(int[] arr){
//细节一:这里可以是arr.length也可以是arr.length-1
for (int i = 0; i < arr.length-1 ; i++) {
int mini = i;
for (int j = i+1; j < arr.length; j++) {
//切换条件,决定升序还是降序
if(arr[mini]>arr[j]) mini =j;
}
swap(arr,mini,i);
}
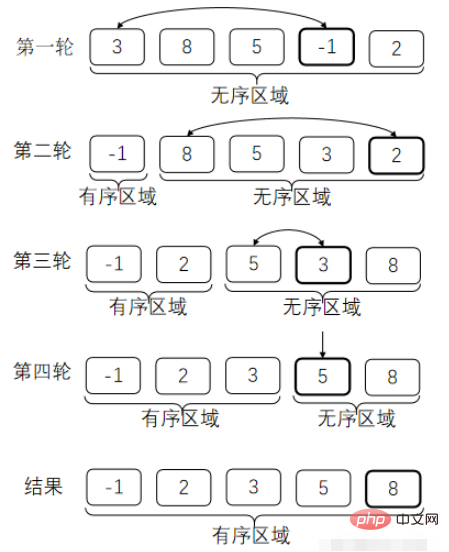
}Comparez tour à tour deux nombres adjacents. Si l'ordre est erroné, échangez-les De cette façon, après chaque tour de comparaison, le plus grand nombre peut être placé là où il devrait être. . (C'est comme amener la plus grosse bulle vers la couche supérieure.)
Voici la signification du mauvais ordre. Nous trions par ordre croissant. Les dernières valeurs doivent être supérieures ou égales aux valeurs précédentes. Sinon, échangez-les.
public static void bubbleSort(int[] arr){
for (int i = 0; i < arr.length-1; i++) {
//记录本次有没有进行交换的操作
boolean flag = false;
//保存在头就动头,保存在尾就动尾
for(int j =0 ; j < arr.length-1-i ; j++){
//升序降序选择地
if(arr[j] > arr[j+1])
{
swap(arr,j,j+1);
flag = true;
}
}
//如果本次没有进行交换操作,表示数据已经有序
if(!flag){break;} //程序结束
}
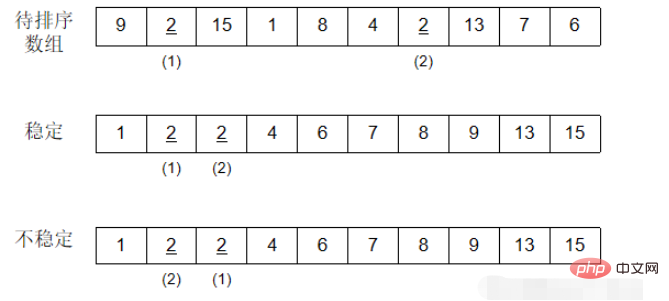
}Le tri par insertion peut en fait être compris comme le processus de tirage de cartes lorsque nous jouons au poker. Lorsque nous tirons des cartes, les cartes dans nos mains sont toujours en ordre chaque fois que nous touchons une carte. , Insérez la carte là où elle doit être. Une fois que toutes les cartes auront été touchées, toutes les cartes seront en ordre.
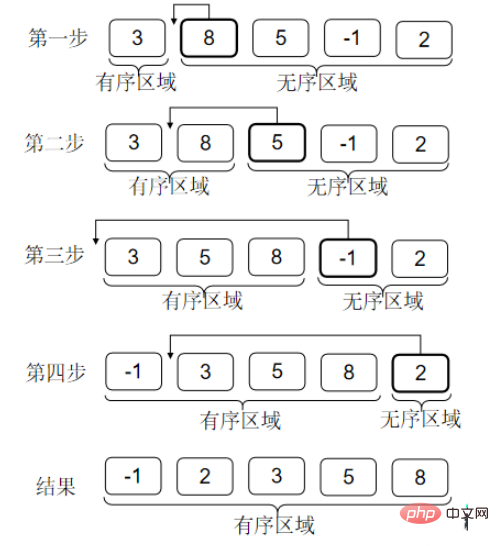
Réflexion : une zone ordonnée est formée devant le tableau. Ensuite, lorsque je trouve la position où le nombre actuel doit être inséré, j'utilise la division binaire. Puis-je optimiser la complexité du tri par insertion en O(nlogn). ?
La position peut être trouvée avec une complexité logarithmique. La clé est que si vous utilisez un tableau pour stocker les données, la complexité du déplacement des données lors de l'insertion est toujours O(n). Si vous utilisez une liste chaînée, trouver la position et l'insérer est O(1), mais la liste chaînée ne peut pas être divisée en deux.
public static void insertSort(int[] arr){
//从第二个数开始,把每个数依次插入到指定的位置
for(int i = 1 ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-1;
//大的后移操作
while(j >= 0 && arr[j] > key)
{
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}Le tri Hill est un algorithme de tri proposé par Donald Shell en 1959. Il s'agit d'une version améliorée et efficace du tri par insertion directe. Le tri en colline nécessite de préparer un ensemble de données sous forme de séquence incrémentielle.
Cet ensemble de données doit remplir les trois conditions suivantes :
1. Les données sont classées par ordre décroissant
2. La valeur maximale des données est inférieure à la longueur du tableau à trier
3. La valeur minimale dans les données est 1.
Les tableaux qui répondent aux exigences ci-dessus peuvent être utilisés comme séquences incrémentielles, mais différentes séquences incrémentielles affecteront l'efficacité du tri. Ici, nous utilisons {5,3,1} comme séquence incrémentielle pour expliquer
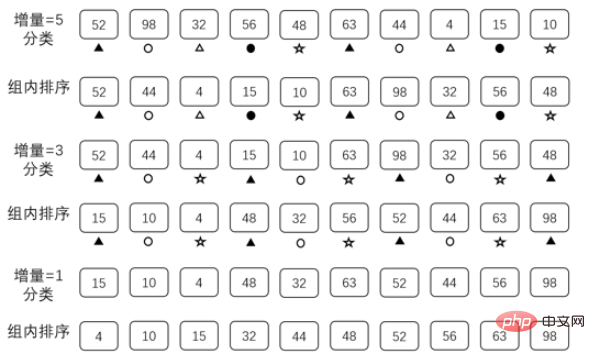
La raison de l'optimisation : réduire la quantité de données pour que la différence entre O(n) et O(n^2) ne soit pas grande
public static void shellSort(int[] arr){
//分块处理
int gap = arr.length/2; //增量
while(1<=gap)
{
//插入排序:只不过是与增量位交换
for(int i = gap ; i < arr.length ; i++)
{
int key = arr[i];
int j = i-gap;
while(j >= 0 && arr[j] > key)
{
arr[j+gap] = arr[j];
j-=gap;
}
arr[j+gap] = key;
}
gap = gap/2;
}
}est un arbre binaire complet, divisé en deux types : grand tas de racines et petit tas de racines
Il peut prendre la valeur maximale/minimale dans O(1), supprimer la valeur maximale/minimale dans O(logn) et supprimez la valeur maximale/minimale dans l'élément d'insertion O(logn)
Opération MIN-HEAPIFY (i) :
Nous supposons que le sous-arbre gauche et le sous-arbre droit d'un certain nœud i dans l'arbre binaire complet les deux satisfont aux propriétés d'un petit tas racine, en supposant que l'enfant gauche du nœud i est left_i, i L'enfant droit du nœud est rigℎt_i. Si a[i] est plus grand que a[left_i] ou a[rigℎt_i], alors le sous-arbre entier avec le nœud i comme nœud racine ne satisfait pas aux propriétés d'un petit tas racine. Nous devons maintenant effectuer une opération : mettre i. en tant que nœud racine Le sous-arbre du nœud racine est ajusté en un petit tas racine.
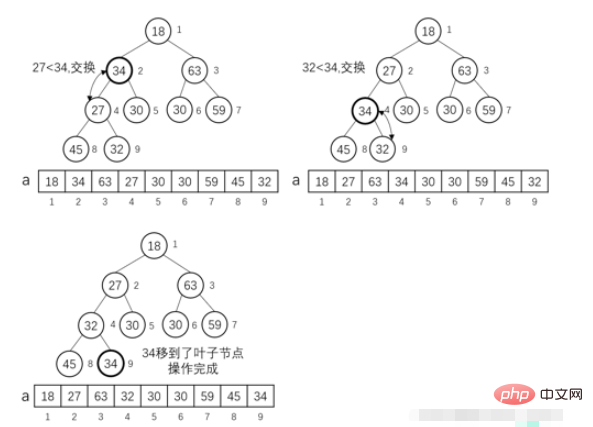
//堆排序
public static void heapSort(int[] arr){
//开始调整的位置为最后一个叶子节点
int start = (arr.length - 1)/2;
//从最后一个叶子节点开始遍历,调整二叉树
for (int i = start; i >= 0 ; i--){
maxHeap(arr, arr.length, i);
}
for (int i = arr.length - 1; i > 0; i--){
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
//将二叉树调整为大顶堆
public static void maxHeap(int[] arr, int size, int index){
//建立左子节点
int leftNode = 2 * index + 1;
//建立右子节点
int rightNode = 2 * index + 2;
int maxNode = index;
//左子节点的值大于根节点时调整
if (leftNode < size && arr[leftNode] > arr[maxNode]){
maxNode = leftNode;
}
//右子节点的值大于根节点时调整
if (rightNode < size && arr[rightNode] > arr[maxNode]){
maxNode = rightNode;
}
if (maxNode != index){
int temp = arr[maxNode];
arr[maxNode] = arr[index];
arr[index] = temp;
//交换之后可能会破坏原来的结构,需要再次调整
//递归调用进行调整
maxHeap(arr, size, maxNode);
}
}J'utilise un gros tas de racines. Le processus de tri se résume à : d'abord la racine gauche puis la racine droite (voyez comment vous l'écrivez) -> (Gauche, droite, haut et bas)
Le tri par fusion est une application typique de la méthode diviser pour régner. Introduisons d'abord la méthode diviser pour régner. La méthode diviser pour régner consiste à diviser un problème complexe. en deux ou plusieurs sous-problèmes identiques ou similaires, puis divisez les sous-problèmes en sous-problèmes plus petits... jusqu'à ce que le sous-problème final soit très petit et puisse être résolu directement, puis les solutions du sous-problème. -les problèmes sont combinés pour obtenir la solution au problème initial.
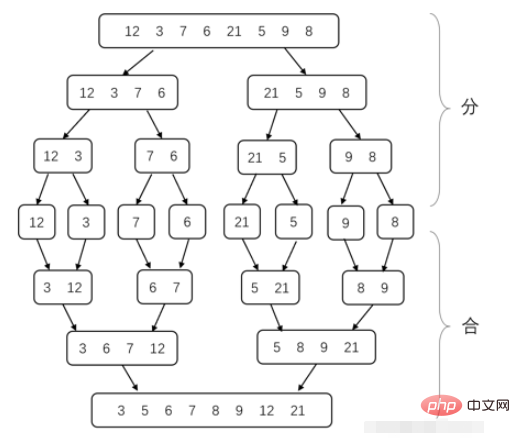
Le processus de sous-problème de décomposition du tri par fusion consiste à diviser le tableau en 2 parties à chaque fois jusqu'à ce que la longueur du tableau soit de 1 (car un tableau avec un seul nombre est ordonné). Fusionnez ensuite les tableaux ordonnés adjacents en un seul tableau ordonné. Jusqu'à ce qu'ils soient tous rassemblés, l'ensemble du tableau est trié. Le problème à résoudre maintenant est de savoir comment fusionner deux tableaux ordonnés en un seul tableau ordonné. En fait, il s'agit de comparer à chaque fois les deux plus petits éléments actuels des deux tableaux. Celui qui est le plus petit est choisi
tableau a | tableau b | Explication | tableau de réponse . |
| 2,5,7 | 1,3,4 | 1<2, prenez 1 et déplacez le pointeur du tableau b vers l'arrière | 1 |
| 2 ,5,7 | 1,3,4 | 2<3, prise 2, le pointeur du tableau a recule | 1,2 |
2,5,7 | 1,3, 4 | 3<5, prise 3, le pointeur du tableau b recule | 1,2,3 |
2,5,7 | 1,3,4 | 4<5, prends 4, déplace le pointeur du tableau b vers l'arrière | 1,2,3,4 |
2,5,7 | 1 ,3,4 | array Il n'y a aucun élément dans b, prenez 5 | 1,2,3,4,5 |
2,5,7 | 1,3, 4 | Il n'y a aucun élément dans le tableau b Oui, prenez 7 | 1,2,3,4,5,7 |
public static void mergeSort(int[] arr, int low, int high){
int middle = (high + low)/2;
if (low < high){
//递归排序左边
mergeSort(arr, low, middle);
//递归排序右边
mergeSort(arr, middle +1, high);
//将递归排序好的左右两边合并
merge(arr, low, middle, high);
}
}
public static void merge(int[] arr, int low, int middle, int high){
//存储归并后的临时数组
int[] temp = new int[high - low + 1];
int i = low;
int j = middle + 1;
//记录临时数组中存放数字的下标
int index = 0;
while (i <= middle && j <= high){
if (arr[i] < arr[j]){
temp[index] = arr[i];
i++;
} else {
temp[index] = arr[j];
j++;
}
index++;
}
//处理剩下的数据
while (j <= high){
temp[index] = arr[j];
j++;
index++;
}
while (i <= middle){
temp[index] = arr[i];
i++;
index++;
}
//将临时数组中的数据放回原来的数组
for (int k = 0; k < temp.length; ++k){
arr[k + low] = temp[k];
}
}快速排序的工作原理是:从待排序数组中随便挑选一个数字作为基准数,把所有比它小的数字放在它的左边,所有比它大的数字放在它的右边。然后再对它左边的数组和右边的数组递归进行这样的操作。
全部操作完以后整个数组就是有序的了。 把所有比基准数小的数字放在它的左边,所有比基准数大的数字放在它的右边。这个操作,我们称为“划分”(Partition)。

//快速排序
public static void QuickSort1(int[] arr, int start, int end){
int low = start, high = end;
int temp;
if(start < end){
int guard = arr[start];
while(low != high){
while(high > low && arr[high] >= guard) high--;
while(low < high && arr[low] <= guard) low++;
if(low < high){
temp = arr[low];
arr[low] = arr[high];
arr[high] = temp;
}
}
arr[start] = arr[low];
arr[low] = guard;
QuickSort1(arr, start, low-1);
QuickSort1(arr, low+1, end);
}
}
//快速排序改进版(填坑法)
public static void QuickSort2(int[] arr, int start, int end){
int low = start, high = end;
if(start < end){
while(low != high){
int guard = arr[start];//哨兵元素
while(high > low && arr[high] >= guard) high--;
arr[low] = arr[high];
while(low < high && arr[low] <= guard) low++;
arr[high] = arr[low];
}
arr[low] = guard;
QuickSort2(arr, start, low-1);
QuickSort2(arr, low+1, end);
}
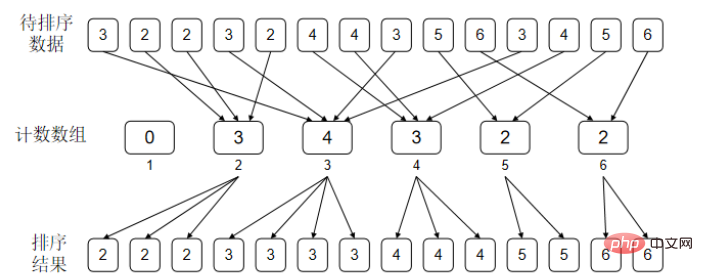
}计算一下每一个数出现了多少次。举一个例子,比如待排序的数据中1出现了2次,2出现了0次,3出现了3次,4出现了1次,那么排好序的结果就是{1.1.3.3.3.4}。
//鸽巢排序
public static void PigeonholeSort(int[] arr){
//获取最大值
int k = 0;
for (int i = 0; i < arr.length; i++) {
k = Math.max(k,arr[i]);
}
//创建计数数组并且初始化为0
int[] cnt = new int[k+10];
for(int i = 0 ; i <= k ; i++) { cnt[i]=0; }
for(int i = 0 ; i < arr.length ;i++) { cnt[arr[i]]++; }
int j = 0;
for(int i = 0 ; i <=k ; i++)
{
while(cnt[i]!=0)
{
arr[j]=i;
j++;
cnt[i]--;
}
}
}鸽巢排序其实算不上是真正意义上的排序算法,它的局限性很大。只能对纯整数数组进行排序,举个例子,如果我们需要按学生的成绩进行排序。是一个学生+分数的结构那就不能排序了。
先考虑这样一个事情:如果对于待排序数据中的任意一个元素 a[i],我们知道有 m 个元素比它小,那么我们是不是就可以知道排好序以后这个元素应该在哪个位置了呢?(这里先假设数据中没有相等的元素)。计数排序主要就是依赖这个原理来实现的。
比如待排序数据是{2,4,0,2,4} 先和鸽巢一样做一个cnt数组{1,0,2,0,2} 0,1,2,3,4
此时cnt[i]表示数据i出现了多少次,
然后对cnt数组做一个前缀和{1,1,3,3,5} :0,1,2,3,4
此时cnt[i]表示数据中小于等于i的数字有多少个
待排序数组 | 计数数组 | 说明 | 答案数组ans |
2,4,0,2,4 | 1,1,3,3,5 | 初始状态 | null,null,null,null,null, |
2,4,0,2,4 | 1,1,3,3,5 | cnt[4]=5,ans第5位赋值,cnt[4]-=1 | null,null,null,null,4 |
2,4,0,2,4 | 1,1,3,3,4 | cnt[2]=3,ans第3位赋值,cnt[2]-=1 | null,null,2 null,4 |
2,4,0,2,4 | 1,1,2,3,4 | cnt[0]=1,ans第1位赋值,cnt[0]-=1 | 0,null,2,null,4 |
2,4,0,2,4 | 0,1,2,3,4 | cnt[4]=4,ans第4位赋值,cnt[4]-=1 | 0,null,2,4,4 |
2,4,0,2,4 | 0,1,2,3,3 | cnt[2]=2,ans第2位赋值,cnt[2]-=1 | 0,2,2,4,4 |
基数排序是通过不停的收集和分配来对数据进行排序的。
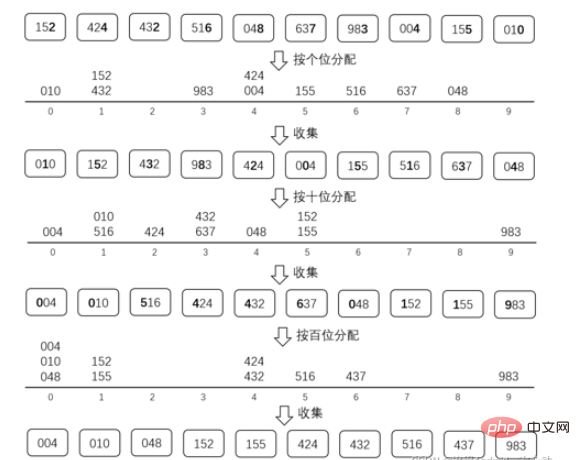
因为是10进制数,所以我们准备十个桶来存分配的数。
最大的数据是3位数,所以我们只需要进行3次收集和分配。
需要先从低位开始收集和分配(不可从高位开始排,如果从高位开始排的话,高位排好的顺序会在排低位的时候被打乱,有兴趣的话自己手写模拟一下试试就可以了)
在收集和分配的过程中,不要打乱已经排好的相对位置
比如按十位分配的时候,152和155这两个数的10位都是5,并且分配之前152在155的前面,那么收集的时候152还是要放在155之前的。
//基数排序
public static void radixSort(int[] array) {
//基数排序
//首先确定排序的趟数;
int max = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
}
int time = 0;
//判断位数;
while (max > 0) {
max /= 10;
time++;
}
//建立10个队列;
List<ArrayList> queue = new ArrayList<ArrayList>();
for (int i = 0; i < 10; i++) {
ArrayList<Integer> queue1 = new ArrayList<Integer>();
queue.add(queue1);
}
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
//分配数组元素;
for (int j = 0; j < array.length; j++) {
//得到数字的第time+1位数;
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
ArrayList<Integer> queue2 = queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
while (queue.get(k).size() > 0) {
ArrayList<Integer> queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!