
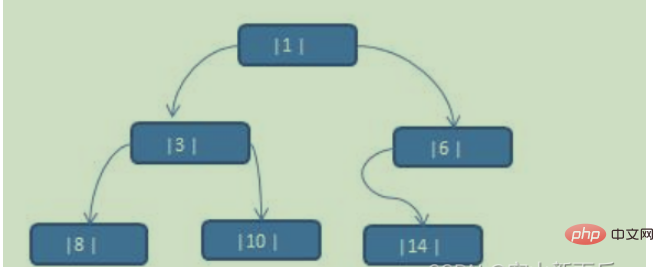
Construisez la séquence {1, 3, 6, 8, 10, 14} dans un arbre binaire.
Analyse du problème :
1. tree Lors du parcours dans l'ordre, le tableau est {8, 3, 10, 1, 6, 14}
2 Cependant, les pointeurs gauche et droit des nœuds 6, 8, 10, 14 ne sont pas entièrement utilisés.
.3. Et si nous voulons utiliser pleinement les pointeurs gauche et droit de chaque nœud afin que chaque nœud puisse pointer vers ses propres nœuds précédents et suivants
4 Solution - Arbre binaire d'indices
Concept : lors de l'utilisation d'un liste chaînée binaire comme structure de stockage d'un arbre binaire, il est facile de trouver les enfants gauche et droit d'un nœud, mais en général, il n'est pas possible de trouver directement les nœuds prédécesseurs et successeurs du nœud dans une certaine séquence de parcours ; . Par conséquent, le threading est utilisé et le champ de pointeur nul de la liste chaînée de la structure arborescente binaire est utilisé pour le threading.
Une liste chaînée binaire de n nœuds contient n+1 [formule 2n-(n-1)=n+1] champs de pointeur nuls. Utilisez le champ de pointeur nul dans la liste chaînée binaire pour stocker des pointeurs vers les nœuds prédécesseurs et successeurs du nœud dans un certain ordre de parcours (ces pointeurs supplémentaires sont appelés « indices »)
Ce type d'indices ajoutés La liste chaînée binaire est appelée une liste chaînée threadée, et l'arbre binaire correspondant est appelé un arbre binaire threadé (Threaded BinaryTree). Selon la nature différente des indices, les arbres binaires d'indices peuvent être divisés en trois types : l'arbre binaire d'indices de pré-ordre, l'arbre binaire d'indices dans l'ordre et l'arbre binaire d'indices de post-ordre
Arbres binaires d'indices dans l'ordre et traversée
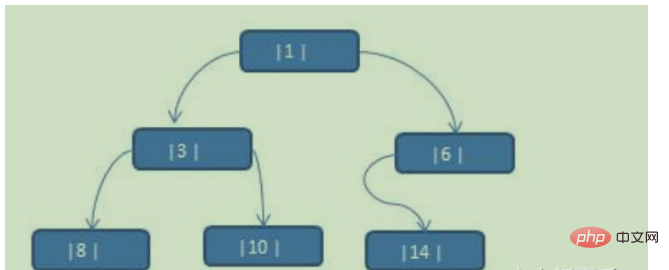
Cas d'application Description : Convertissez l'arbre binaire suivant en un arbre binaire d'indices dans l'ordre. La séquence numérique du parcours dans l'ordre est {8, 3, 10, 1, 14, 6}
Pensez à l'analyse
Le résultat du parcours dans l'ordre : {8, 3, 10, 1, 14, 6}
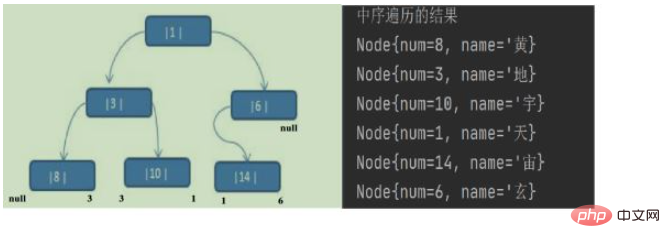
Ensuite, les pointeurs gauche et droit de l'arbre binaire après le threading sont comme indiqué dans la figure ci-dessus↑
Explication : Lorsque l'arbre binaire est threadé, les attributs gauche et droit du nœud Node ont les éléments suivants situations :
gauche pointe vers le sous-arbre gauche, Il peut également s'agir du nœud prédécesseur pointé. Par exemple, le sous-arbre gauche du nœud ① pointe vers le sous-arbre gauche et la gauche du nœud ⑩ pointe vers le nœud prédécesseur.
right pointe vers le sous-arbre droit, ou il peut pointer vers le nœud successeur, tel que le nœud ① right pointe vers le sous-arbre droit, et la droite du nœud ⑩ pointe vers le nœud successeur.
Donc nous besoin de changer la structure des nœuds de l'arbre binaire d'origine
package com.studySelf.tree.threadedBinaryTree; /** * @author wang * @version 1.0 * @packageName com.studySelf.tree.tree01 * @className Node * @date 2022/4/19 20:15 * @Description Node结点 */ public class Node { //唯一编号 private int num; //结点的值 private String name; //左结点 private Node left; //右节点 private Node right; //这个属性用来控制线索二叉树的结点的指向,0代表指向左结点,1代表指向前趋结点 private int leftType; //这个属性用来控制线索二叉树的结点的指向,0代表指向右结点,1代表指向后继结点 private int rightType; //构造方法 public Node(int num, String name) { this.num = num; this.name = name; } public int getLeftType() { return leftType; } public void setLeftType(int leftType) { this.leftType = leftType; } public int getRightType() { return rightType; } public void setRightType(int rightType) { this.rightType = rightType; } public int getNum() { return num; } public void setNum(int num) { this.num = num; } public String getName() { return name; } public void setName(String name) { this.name = name; } public Node getLeft() { return left; } public void setLeft(Node left) { this.left = left; } public Node getRight() { return right; } public void setRight(Node right) { this.right = right; } @Override public String toString() { return "Node{" + "num=" + num + ", name='" + name + '}'; } /** * 前序遍历 */ public void preSelect() { //首先输出根结点 System.out.println(this); //其次判断是否有左结点 if (this.left != null) { //没有左结点,就递归调用本方法输出该结点。 this.left.preSelect(); } if (this.right != null) { this.right.preSelect(); } } /** * 中序遍历 */ public void infixSelect() { //首先判断左结点 if (this.left != null) { //如果左结点不为空,递归向左子树调用 this.left.infixSelect(); } //当左结点为空,再输出根结点。当他本身就是最后一个左结点的时候,会直接输出,且没有右节点 System.out.println(this); if (this.right != null) { //右节点同样如此,递归调用。直到没有结点为止。 this.right.infixSelect(); } } /** * 设二叉树有三个结点,根结点,左结点,右节点。 * 后序遍历,解释,当一个二叉树的左结点不为空,那么他会进入下一个递归调用自己的后序遍历方法 * 此时,根结点就是左结点,这时判断左结点,右节点均为空,就会输出左结点 * 回退到根结点为this的时候,左结点已经判断完毕,接下来是右节点,右节点不为空,进入后续遍历递归, * 此时的this就是右节点,进入递归后,判断,不存在左右结点,输出this,也就是整个二叉树的右节点 * 回退到this为根结点时,右节点也已经输出,走到最后一步,输出自己也就是this。 * 整个后序遍历就结束,那么该二叉树的遍历结果就是左,右,根 */ public void afterSelect() { if (this.left != null) { this.left.afterSelect(); } if (this.right != null) { this.right.afterSelect(); } System.out.println(this); } /** * @param num * @Date 2022/4/21 17:51 * @Param * @Return Node * @MetodName preSearchByNum * @Author wang * @Description 根据结点的编号来查询结点, 前序遍历查询,根,左,右 */ public Node preSearchByNum(int num) { //首先判断传进来的num与该结点的num是否相等 //如果相等,那该结点就是我们要找的结点。 if (this.num == num) { return this; } //如果不相等,该结点就不是我们要找的结点 //那么我们就遍历该结点的左子节点,和右子结点 //定义一个结点用于接收最后的返回结果 Node resultNode = null; //如果该结点的左子结点不为空,就递归调用前序遍历,继续查找,如果找到了,那么resultNode就是我们想要的值 if (this.left != null) { resultNode = this.left.preSearchByNum(num); } //如果遍历完左子结点,已经找到了我们想要的结果,直接返回结果即可, if (resultNode != null) { return resultNode; } //如果左子结点为空,且没有找到我们想要的结点的情况下。那就判断右子结点 if (this.right != null) { resultNode = this.right.preSearchByNum(num); } //最后,如果找到了,那么resultNode一定会被赋值,如果没找到,就会返回null return resultNode; } /** * @param num * @Date 2022/4/21 17:58 * @Param * @Return Node * @MetodName infixSearchByNum * @Author wang * @Description 中序遍历查找,左,根,右进行查询即可。 */ public Node infixSearchByNum(int num) { //首先判断左子结点,如果存在左子结点,递归继续查询遍历即可即可。 Node resultNode = null; if (this.left != null) { resultNode = this.left.infixSearchByNum(num); } //如果左子结点已经找到了我们想要的结点,直接返回当前结点即可 if (resultNode != null) { return resultNode; } //判断根结点 if (this.num == num) { return this; } //判断右子结点, if (this.right != null) { resultNode = this.right.infixSearchByNum(num); } //最后返回我们的结果即可。 return resultNode; } /** * @param num * @Date 2022/4/21 19:15 * @Param * @Return Node * @MetodName afterSearchNum * @Author wang * @Description 后续遍历结点进行查找结点。左,右,根 */ public Node afterSearchNum(int num) { Node resultNode = null; //首先遍历左结点 if (this.left != null) { resultNode = this.left.afterSearchNum(num); } //判断左结点是否找到哦啊 if (resultNode != null) { return resultNode; } //判断右节点是否为空 if (this.right != null) { resultNode = this.right.afterSearchNum(num); } //判断右节点是否找到 if (resultNode != null) { return resultNode; } //判断根结点是否为我们找的结点 if (this.num == num) { return this; } //最后返回 return resultNode; } /** * @param num * @Date 2022/4/25 19:30 * @Param * @Return void * @MetodName delNodeByNum * @Author wang * @Description 根据结点的编号删除结点 */ public void delNodeByNum(int num) { //首先,判断当前结点的左结点是否为空,并且左结点的num是否与num相等 if (this.left != null && this.left.num == num) { //如果相等,那就说明该结点就是我们要删除的结点,将其左结点置空即可 this.left = null; return; } //如果左结点没有执行,说明左结点没有我们想要的结果,也就是要删除的结点不在左结点 //那么就对右节点进行判断 if (this.right != null && this.right.num == num) { this.right = null; return; } //如果左右结点均没有找到目标结点 //那么就对左子树进行递归删除操作 if (this.left != null) { this.left.delNodeByNum(num); } //同理,如果左子树没有目标结点,向右子树进行递归删除操作 if (this.right != null) { this.right.delNodeByNum(num); } } }
Vous pouvez voir que nous avons ces deux attributs supplémentaires :
//这个属性用来控制线索二叉树的结点的指向,0代表指向左结点,1代表指向前趋结点 private int leftType; //这个属性用来控制线索二叉树的结点的指向,0代表指向右结点,1代表指向后继结点 private int rightType;
Arbre binaire fileté dans l'ordre
/**中序线索化二叉树*/ /** * @param node 该结点为根结点,从根节点开始线索化二叉树,中序 */ public void infixThreadNodes(Node node) { /**首先判断二叉树的根节点上会否为空,如果根结点为空,不可以线索化,因为没有二叉树*/ if (node == null) { return; } /**接着对左子树进行线索化*/ infixThreadNodes(node.getLeft()); /**对当前结点进行线索化*/ /**首先判断当前结点的左子结点是否为空*/ if (node.getLeft() == null) { //如果左子结点为空,说明就找到了我们需要线索化的结点 //就可以将pre也就是一直在当前结点的前趋结点设置给当前结点的左子结点, //如果这是第一个结点,那么pre为空,正好第一个结点的前趋结点也为空 node.setLeft(pre); //并且将它的左子结点的类型设置为前趋结点。1代表前趋结点 node.setLeftType(1); } /**接着判断前趋结点的右子结点是否为空,前提是前趋结点不能为空,如果他为空,说明这是第一个结点还没走完*/ if (pre != null && pre.getRight() == null) { //如果条件满足,说明前趋结点现在已经走到了值,并且还没有线索到后继结点, // 也就是当前结点的上一个结点(这个上一个结点就是当前的前趋结点)还没有后继, //那么上一个结点的后继结点就是当前结点,因此赋值前趋结点(也就是上一个结点)的后继结点为当前结点。 //这样这条线索就连接上了,并且只有满足叶子结点的结点才可以进行线索化 pre.setRight(node); pre.setRightType(1); } //当前两步走完之后,就可以将pre结点赋值为当前结点, // 因为下一个结点一走,当前结点就是前趋结点了。直到走到全部线索化结束 //这步十分重要,这一步不写,整个线索化就连接不上 pre = node; /**对右子树进行线索化*/ infixThreadNodes(node.getRight()); }
Idée d'arbre binaire fileté d'ordre moyen
Parce que l'ordre de l'arbre binaire parcouru dans l'ordre est la racine gauche et la droite, par conséquent, enfilez d'abord le sous-arbre gauche et enfilez-le récursivement
Lors d'une récurrence vers le nœud le plus à gauche du sous-arbre gauche, son nœud gauche doit être vide, puis son nœud gauche reçoit la valeur pre (le nœud pré reçoit la valeur actuelle dans la dernière étape du nœud de thread, afin que la récursion puisse continuer), notez que le type du nœud gauche doit être changé en 1, ce qui signifie qu'il s'agit du nœud prédécesseur. Le nœud prédécesseur a perdu la trace.
Le traitement du nœud successeur consiste à déterminer le nœud prédécesseur. Si le nœud de tendance actuel n'est pas vide et que le nœud droit du nœud prédécesseur est vide, définissez le nœud droit du nœud prédécesseur comme nœud actuel. .C'est-à-dire que le nœud droit du nœud précédent qui n'a pas été défini, le type doit également être défini sur successeur
La dernière étape consiste à attribuer une valeur au nœud pré, qui est le nœud actuel, car le prochaine récursion, le nœud actuel devient le nœud précédent. Le point, qui est le pré
ici, doit enfin indiquer le nœud enfant droit de l'arbre binaire.
Parcours d'arbres binaires filetés dans l'ordre
Lors du parcours d'un arbre binaire fileté dans l'ordre, il doit d'abord être clair que l'ordre de parcours doit être le même que le résultat du parcours du binaire dans l'ordre d'origine arbre, alors le parcours sera réussi
Ensuite, la première étape devrait être de déterminer que le nœud racine n'est pas vide, ce qui est la condition de fin de boucle
Ensuite, nous bouclons pour trouver le nœud enfant gauche du courant nœud dont le type est 0, c'est-à-dire le nœud qui n'a pas été threadé. Point, tant qu'il est 0, le nœud attribuera toujours des valeurs au nœud enfant de gauche. Jusqu'à ce que nous trouvions le premier nœud threadé et le produisions, ce sera notre premier nœud threadé et le premier nœud enfant gauche du parcours dans l'ordre.
Après la sortie, déterminez si son nœud enfant droit est threadé. S'il est threadé, alors le nœud de nœud actuel est attribué comme son propre nœud enfant droit et indique si le nœud qui le suit est le type du bon enfant. le nœud est à nouveau 1, puis continuez à revenir en arrière et à attribuer des valeurs, indiquant qu'il a un successeur
jusqu'à ce que le type du nœud enfant droit soit 0. Après avoir quitté la boucle, vous devez également attribuer des valeurs à droite et continuez vers Post traversal
démonstration de code
/**遍历中序线索化二叉树*/ public void infixThreadNodesSelect() { /**第一个结点为根结点*/ Node node = root; while(node != null) { /**当结点不为空,就一直遍历*/ /**当该结点的左子结点的类型为1的时候,也就是说该结点是被线索化的结点, * 因为是中序遍历,所以应该遍历到最左边的最左子结点,那么就是第一个 * 左子结点类型为1的结点。*/ while(node.getLeftType() == 0) { node = node.getLeft(); } /**当左子结点的类型为1,输出左子结点*/ System.out.println(node); /**当右子结点类型为1,当前结点输出完毕后 * 中序遍历就应该输出右子结点,那么就是当前结点的右子结点类型只要为1,就往后移动 * 并且输出,当他为0,说明没有线索化,那么没有后继结点,但是他有右子结点, * 因此要在循环结束以后向后移动。*/ while (node.getRightType() == 1) { node = node.getRight(); System.out.println(node); } /**当右子结点循环退出,说明这里到了类型为0也就是后继结点*/ node = node.getRight(); }
arbre binaire threadé
./** * 前序线索化二叉树 */ public void preThreadNodes(Node node) { /**首先判断当前节点是否为空*/ if (node == null) { return; } /**如果是前序遍历,那么先对当前结点进行判断,当前结点的前趋结点的操作*/ if (node.getLeft() == null) { node.setLeft(pre); node.setLeftType(1); } /**处理后继结点,定义的前趋结点不为空,说明他有值,就是已经存在了上一个结点的值,他的右子结点没有值的话,就可以 * 给他赋予后继结点为当前结点,这里赋予的也就是上一个结点*/ if (pre != null && pre.getRight() == null) { pre.setRight(node); pre.setRightType(1); } /**这里是关键的一步*/ pre = node; /**对左子结点进行线索化,注意,这里需要排除已经被线索化掉的结点,因为这里要考虑一个情况, * 比如这里已将到了最下面一个左子结点,由于是前序遍历,遍历到左子结点,他的前趋结点在上面就设置了 * 如果这里不判断左子结点的类型,那么就会进入递归,但是这个递归如果进去了,就是错误的递归,因为他传过去的结点 * 是我们刚刚给他赋值的前趋结点,也就是根结点。会发生错误。因此得判断类型*/ if (node.getLeftType() != 1) { preThreadNodes(node.getLeft()); } /**对右子结点进行递归线索化*/ if (node.getRightType() != 1) { preThreadNodes(node.getRight()); } }
遍历线索化二叉树
/** * 前序遍历线索二叉树*/ public void preThreadNodeSelect() { Node node = root; while(node !=null) { while(node.getLeftType() == 0) { /**前序遍历为根左右,先输出根结点,因为他每次进来循环肯定是先到根结点,所以一进该循环 * 就要输出根结点,当他的lefttype=1循环结束,说明遇到了被线索化的地方了。*/ System.out.println(node); /**再最左子结点进行遍历*/ node = node.getLeft(); } /**上面的循环结束之后就应该输出当前结点,也就是那个序列化的结点 * 之后结点向右移动继续遍历*/ System.out.println(node); node = node.getRight(); } }
图解
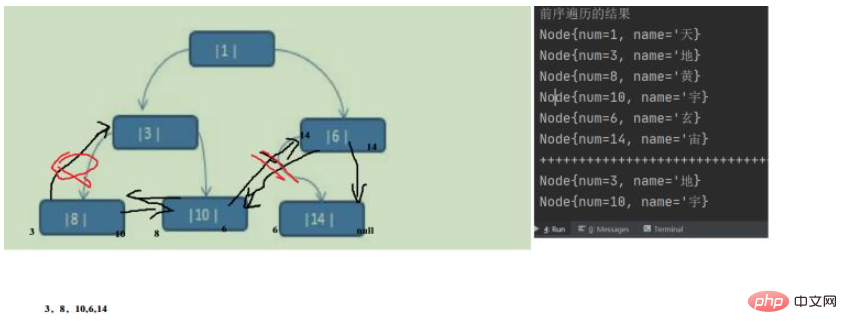
后续线索化二叉树
/** * 后序线索化二叉树的方法 */ public void postThreadedBinaryTree(Node node) { /**首先判断结店不能为空*/ if (node == null) { return; } /**先后续线索化左子结点*/ postThreadedBinaryTree(node.getLeft()); /**在后续线索化右子结点*/ postThreadedBinaryTree(node.getRight()); /**处理当前结点的前趋结点*/ if (node.getLeft() == null) { node.setLeft(pre); node.setLeftType(1); } /**处理后继结点*/ if (pre != null && pre.getRight() == null) { pre.setRight(node); pre.setRightType(1); } pre = node; }
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!