
L'index est trié à l'avance, de sorte que des algorithmes à haute efficacité tels que la recherche binaire puissent être appliqués lors de la recherche. La complexité de la recherche séquentielle générale est O(n), tandis que la complexité de la recherche binaire est O(log2n) ; lorsque n est très grand, la différence d'efficacité entre les deux est énorme.

L'environnement d'exploitation de ce tutoriel : système windows7, version mysql8, ordinateur Dell G3.
Mysql est une base de données très populaire sur Internet. La conception de son moteur de stockage sous-jacent et de son moteur de récupération de données est très importante. En particulier, la forme de stockage des données Mysql et la conception de l'index déterminent les performances globales de récupération des données de Mysql. .
Nous savons que la fonction d'un index est de récupérer rapidement des données, et l'essence d'une récupération rapide est la structure des données. Grâce à la sélection de différentes structures de données, diverses données peuvent être rapidement récupérées. Dans la base de données, des algorithmes de recherche efficaces sont très importants, car une grande quantité de données est stockée dans la base de données et un index efficace peut faire gagner énormément de temps. Par exemple, dans le tableau de données suivant, si Mysql n'implémente pas l'algorithme d'indexation, alors pour trouver les données avec id=7, vous ne pouvez utiliser qu'un parcours séquentiel violent pour trouver les données. Pour trouver les données avec id=7, vous pouvez uniquement utiliser un parcours séquentiel violent pour trouver les données. Il faut le comparer 7 fois. Si cette table stocke 10 millions de données. Pour rechercher les données avec id=1000W, elles seront comparées 1000W fois. Cette vitesse est inacceptable.
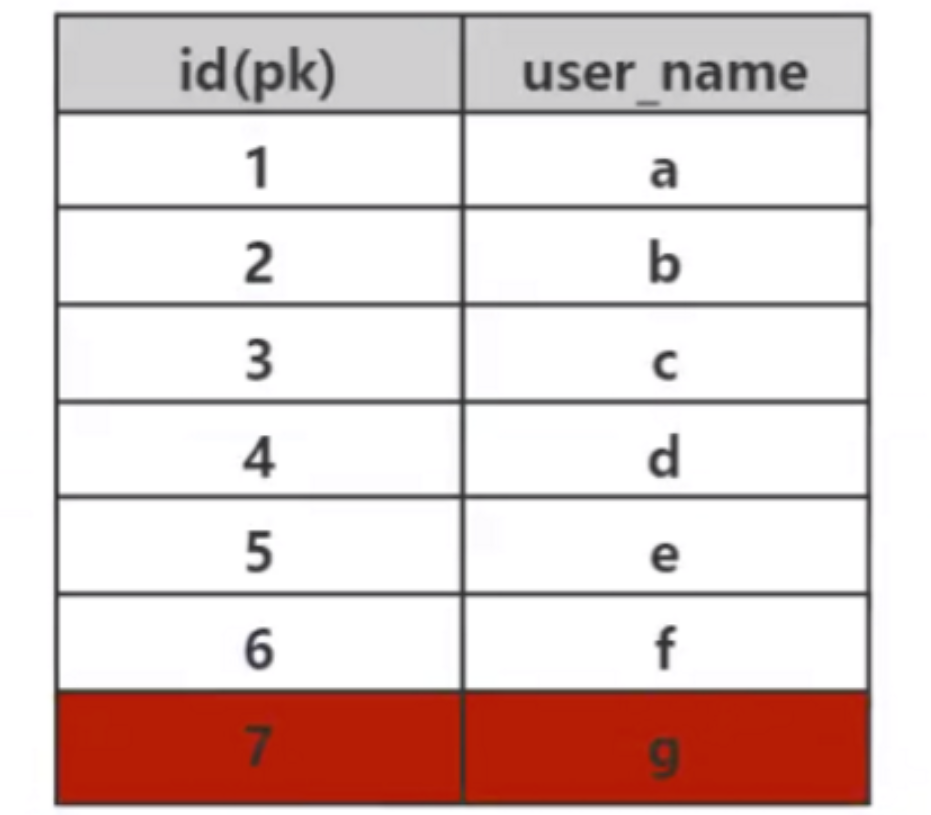
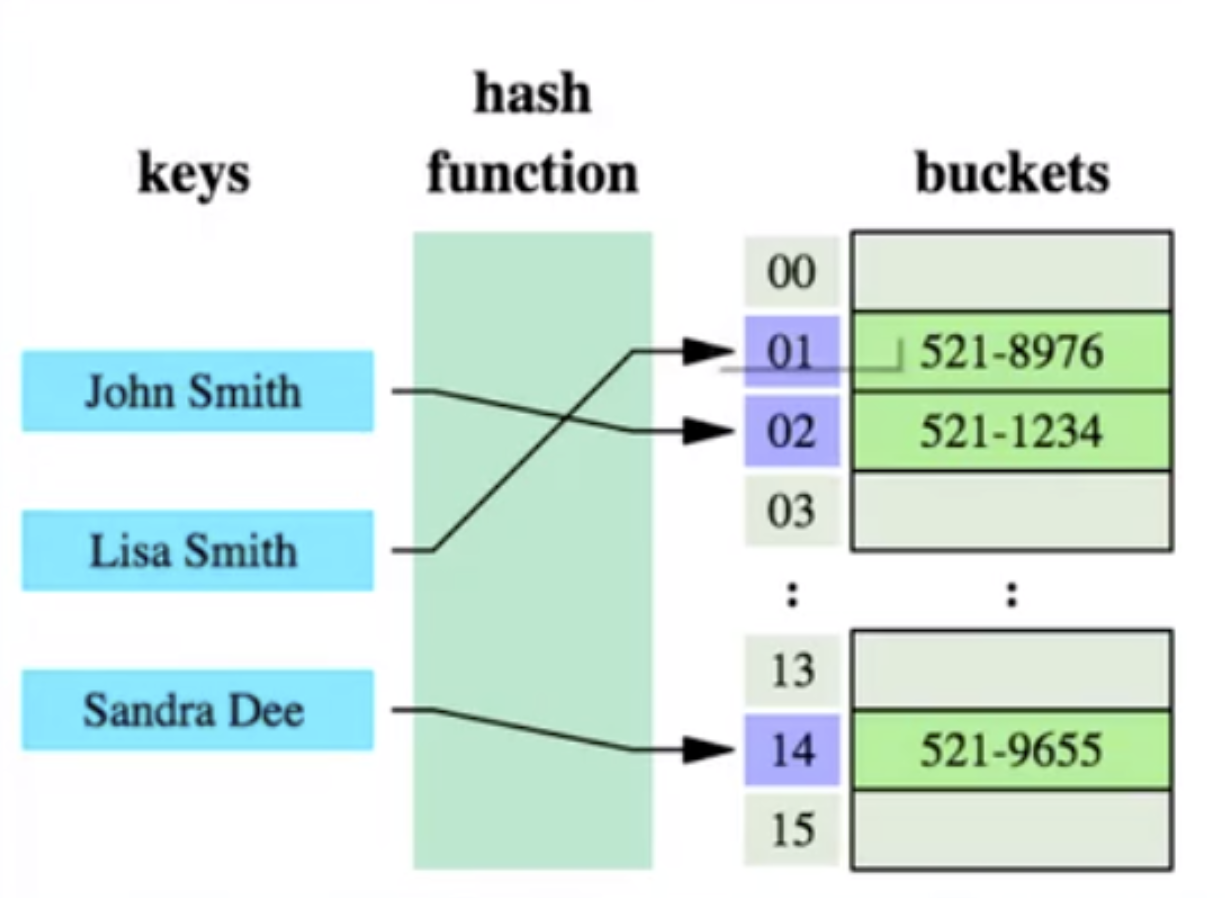
Table de hachage (Hash)
La table de hachage est un outil efficace pour une récupération rapide des données.
Algorithme de hachage : également appelé algorithme de hachage, il convertit n'importe quelle valeur (clé) en une adresse de clé de longueur fixe via une fonction de hachage et utilise cette adresse pour créer une structure de données pour des données spécifiques.
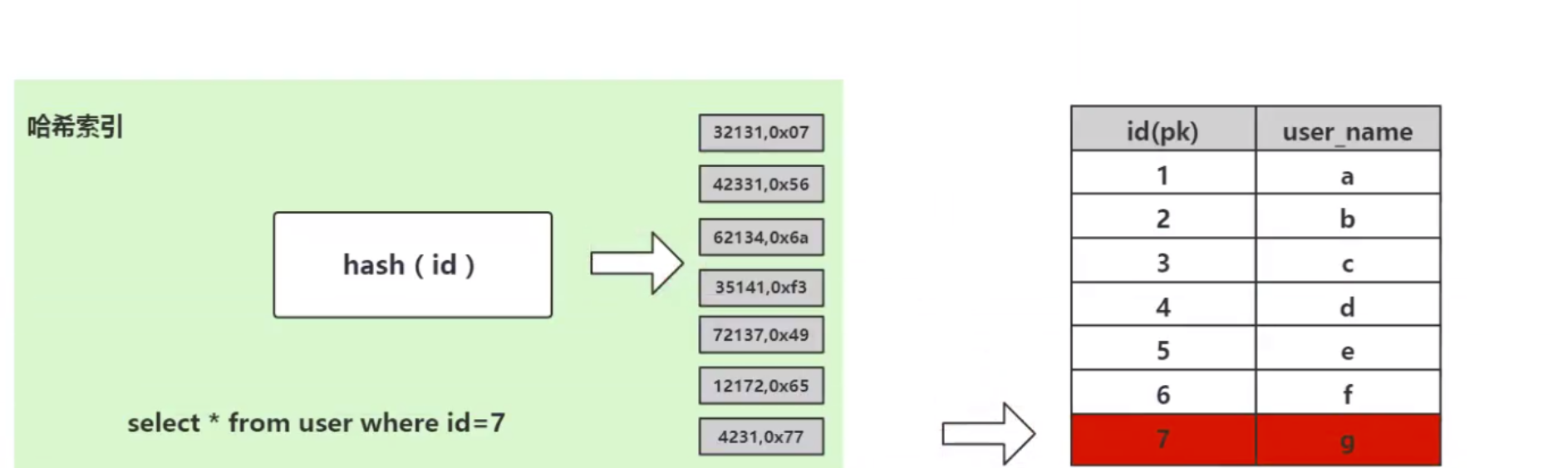
Considérez cet utilisateur de table de base de données. Il y a 7 données dans la table. Nous devons récupérer les données avec l'id=7. La syntaxe SQL est :
select * from user where id=7;
L'algorithme de hachage calcule et stocke d'abord le. data avec id=7 L'adresse physique addr=hash(7)=4231, et l'adresse physique mappée par 4231 est 0x77 est l'adresse physique des données stockées avec id=7 Les données correspondant à user_name='g'. peuvent être trouvés via cette adresse indépendante. Il s'agit du processus de calcul utilisé par l'algorithme de hachage pour récupérer rapidement les données.
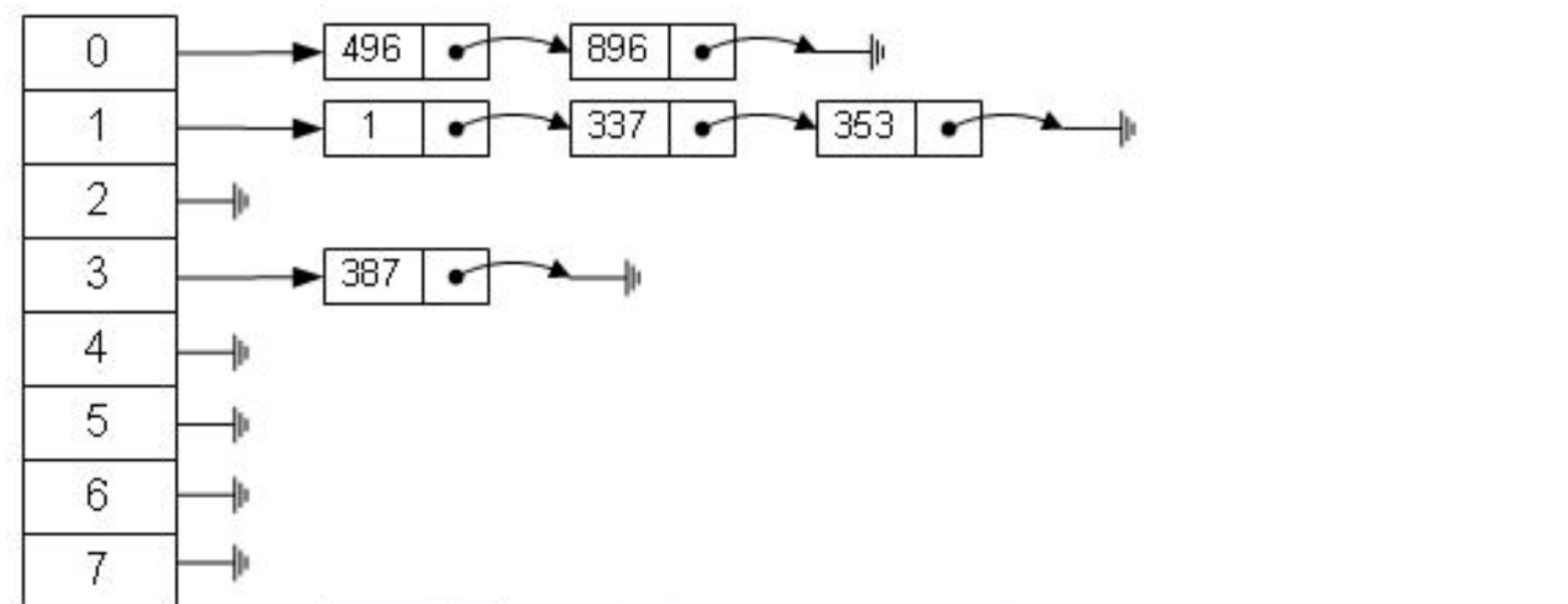
Mais l'algorithme de hachage a un problème de collision de données, c'est-à-dire que la fonction de hachage peut calculer le même résultat pour différentes clés. Par exemple, hash(7) peut calculer le même résultat que hash(199), qui est différent de la clé. est mappé au même résultat, ce qui est un problème de collision. Un moyen courant de résoudre le problème de collision est la méthode d'adresse en chaîne, qui utilise une liste chaînée pour connecter les données en collision. Après avoir calculé la valeur de hachage, vous devez également vérifier si la valeur de hachage a une collision dans la liste chaînée des données. Si tel est le cas, elle sera parcourue jusqu'à la fin de la liste chaînée jusqu'à ce que les données correspondant à la clé réelle soient trouvées.
从算法时间复杂度分析来看,哈希算法时间复杂度为 O(1),检索速度非常快。比如查找 id=7 的数据,哈希索引只需要计算一次就可以获取到对应的数据,检索速度非常快。但是 Mysql 并没有采取哈希作为其底层算法,这是为什么呢?
因为考虑到数据检索有一个常用手段就是范围查找,比如以下这个 SQL 语句:
select * from user where id \>3;
针对以上这个语句,我们希望做的是找出 id>3 的数据,这是很典型的范围查找。如果使用哈希算法实现的索引,范围查找怎么做呢?一个简单的思路就是一次把所有数据找出来加载到内存,然后再在内存里筛选筛选目标范围内的数据。但是这个范围查找的方法也太笨重了,没有一点效率而言。
所以,使用哈希算法实现的索引虽然可以做到快速检索数据,但是没办法做数据高效范围查找,因此哈希索引是不适合作为 Mysql 的底层索引的数据结构。
二叉查找树(BST)
二叉查找树是一种支持数据快速查找的数据结构,如图下所示:
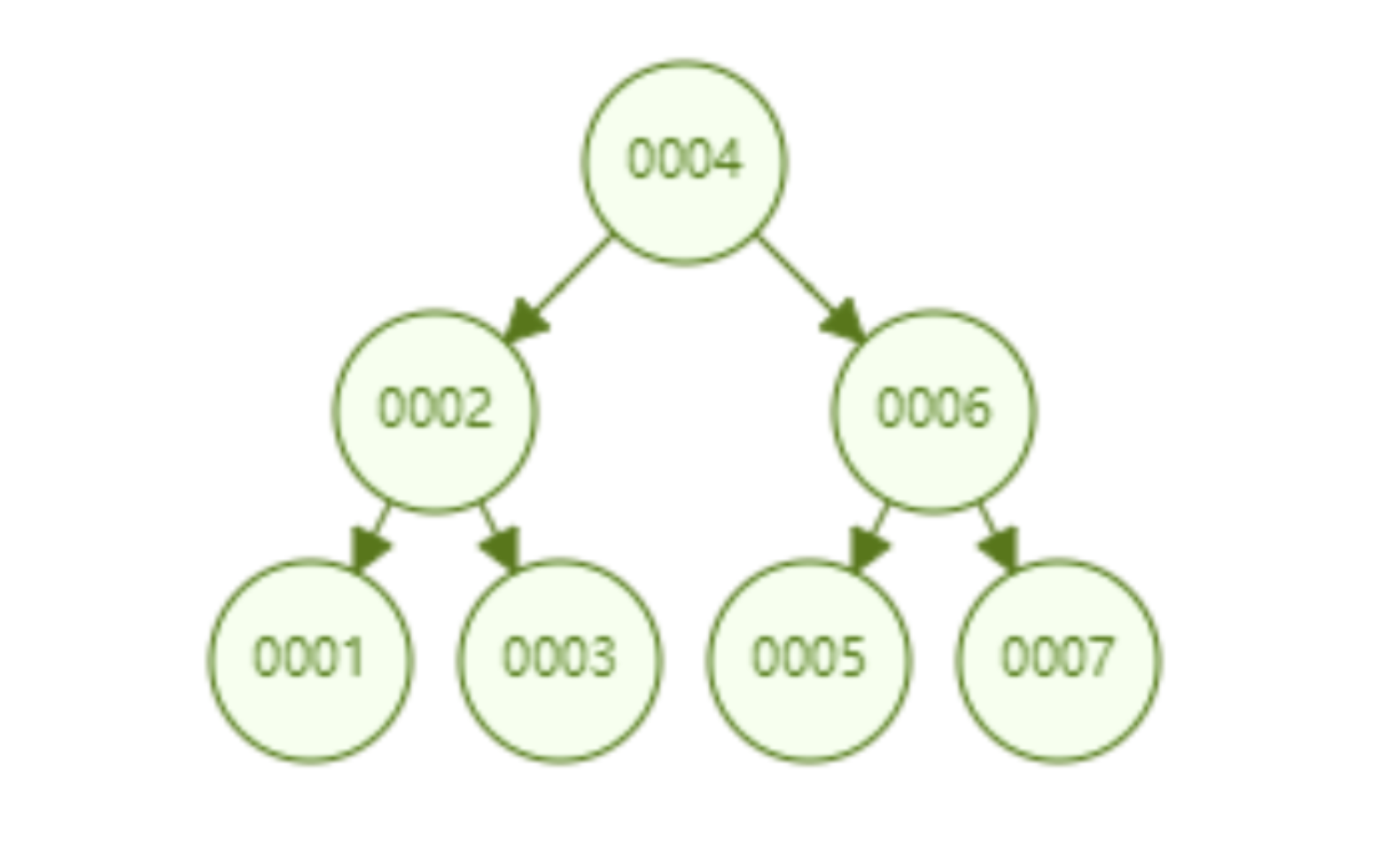
二叉查找树的时间复杂度是 O(lgn),比如针对上面这个二叉树结构,我们需要计算比较 3 次就可以检索到 id=7 的数据,相对于直接遍历查询省了一半的时间,从检索效率上看来是能做到高速检索的。此外二叉树的结构能不能解决哈希索引不能提供的范围查找功能呢?
答案是可以的。观察上面的图,二叉树的叶子节点都是按序排列的,从左到右依次升序排列,如果我们需要找 id>5 的数据,那我们取出节点为 6 的节点以及其右子树就可以了,范围查找也算是比较容易实现。
但是普通的二叉查找树有个致命缺点:极端情况下会退化为线性链表,二分查找也会退化为遍历查找,时间复杂退化为 O(N),检索性能急剧下降。比如以下这个情况,二叉树已经极度不平衡了,已经退化为链表了,检索速度大大降低。此时检索 id=7 的数据的所需要计算的次数已经变为 7 了。
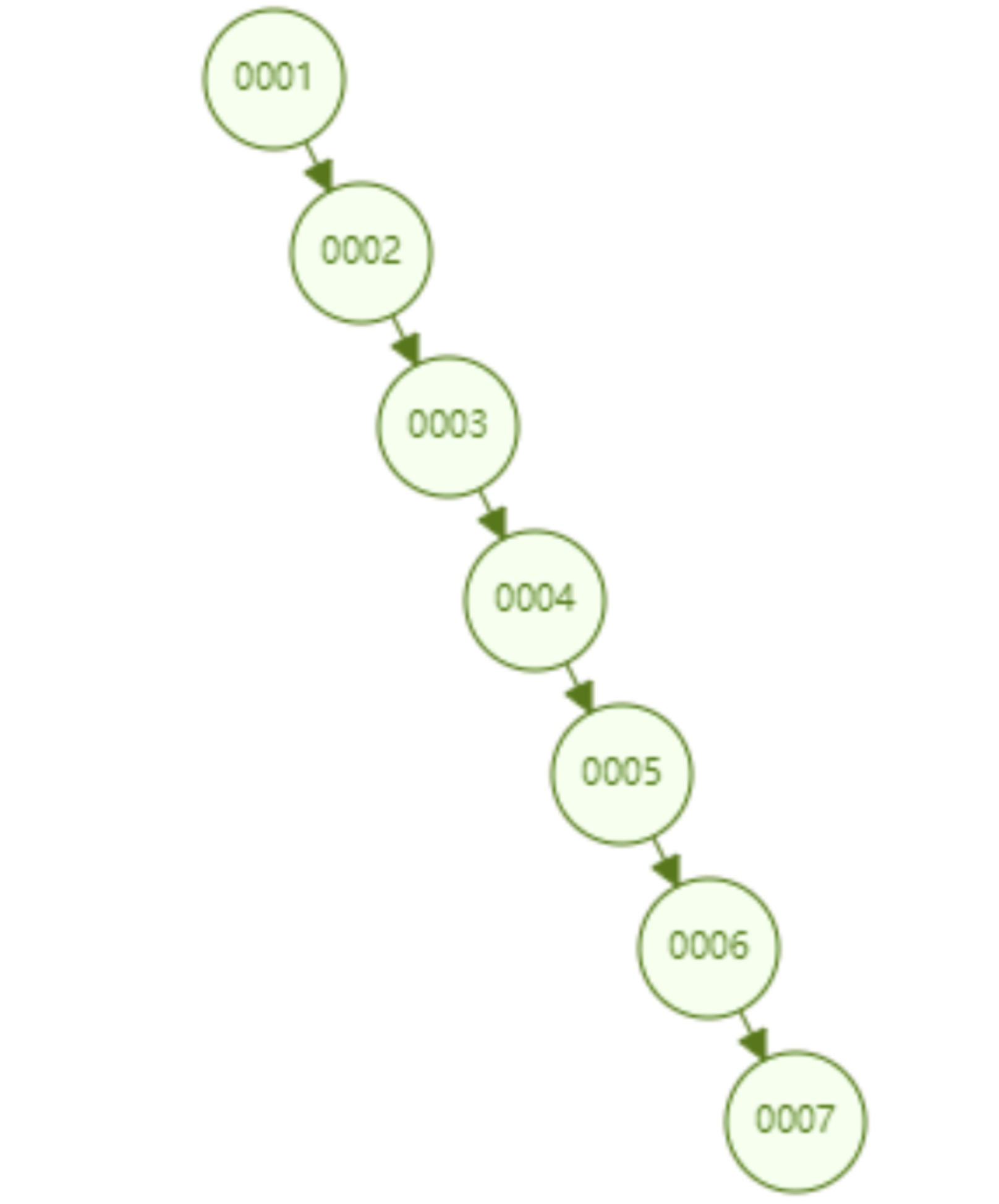
Dans les bases de données, l'auto-incrémentation des données est une forme très courante. Par exemple, la clé primaire d'une table est id, et la clé primaire est généralement auto-incrémentée par défaut dans le cas d'une structure de données. l'arbre binaire est utilisé comme index, Ensuite, le problème de recherche linéaire causé par l'état déséquilibré introduit ci-dessus se produira inévitablement. Par conséquent, un simple arbre de recherche binaire présente le problème de performances de récupération réduites causées par un déséquilibre et ne peut pas être directement utilisé pour implémenter l'index sous-jacent de Mysql.
Arbres AVL et arbres rouge-noir
Les arbres de recherche binaires ont des problèmes de déséquilibre. Par conséquent, les chercheurs proposent que grâce à la rotation et à l'ajustement automatiques des nœuds de l'arbre, l'arbre binaire peut toujours maintenir un état fondamentalement équilibré, et le L'arbre de recherche binaire peut être conservé. Les arbres de recherche pour des performances de recherche optimales. Les arbres binaires à l'état d'équilibre auto-ajustables basés sur cette idée comprennent les arbres AVL et les arbres rouge-noir.
Tout d'abord, présentons brièvement l'arbre rouge-noir. Il s'agit d'une structure arborescente qui ajuste automatiquement la forme de l'arbre. Par exemple, lorsque l'arbre binaire est dans un état déséquilibré, l'arbre rouge-noir pivote automatiquement vers la gauche et. Les nœuds de droite et les nœuds changeront de couleur pour ajuster la forme de l'arbre, afin de maintenir un état d'équilibre de base (la complexité temporelle est O (logn)), ce qui garantit que l'efficacité de la recherche ne sera pas réduite de manière significative. Par exemple, si les nœuds de données sont insérés dans l'ordre croissant de 1 à 7, un arbre de recherche binaire ordinaire dégénérera en une liste chaînée, mais un arbre rouge-noir ajustera continuellement la forme de l'arbre pour maintenir un équilibre de base, comme illustré. dans la figure ci-dessous. Le nombre de nœuds à comparer lors de la recherche de id=7 dans l'arbre rouge-noir ci-dessous est de 4, ce qui maintient toujours la bonne efficacité de recherche de l'arbre binaire.
L'arbre rouge-noir a une bonne efficacité de recherche moyenne, et il n'y a pas de situation O(n) extrême. Alors, l'arbre rouge-noir peut-il être utilisé comme implémentation d'index sous-jacente de Mysql ? En fait, les arbres rouge-noir ont aussi quelques problèmes. Regardez l’exemple suivant.
L'arbre rouge-noir insère 1 à 7 nœuds séquentiellement et le nombre de nœuds qui doivent être calculés lors de la recherche de id=7 est de 4.
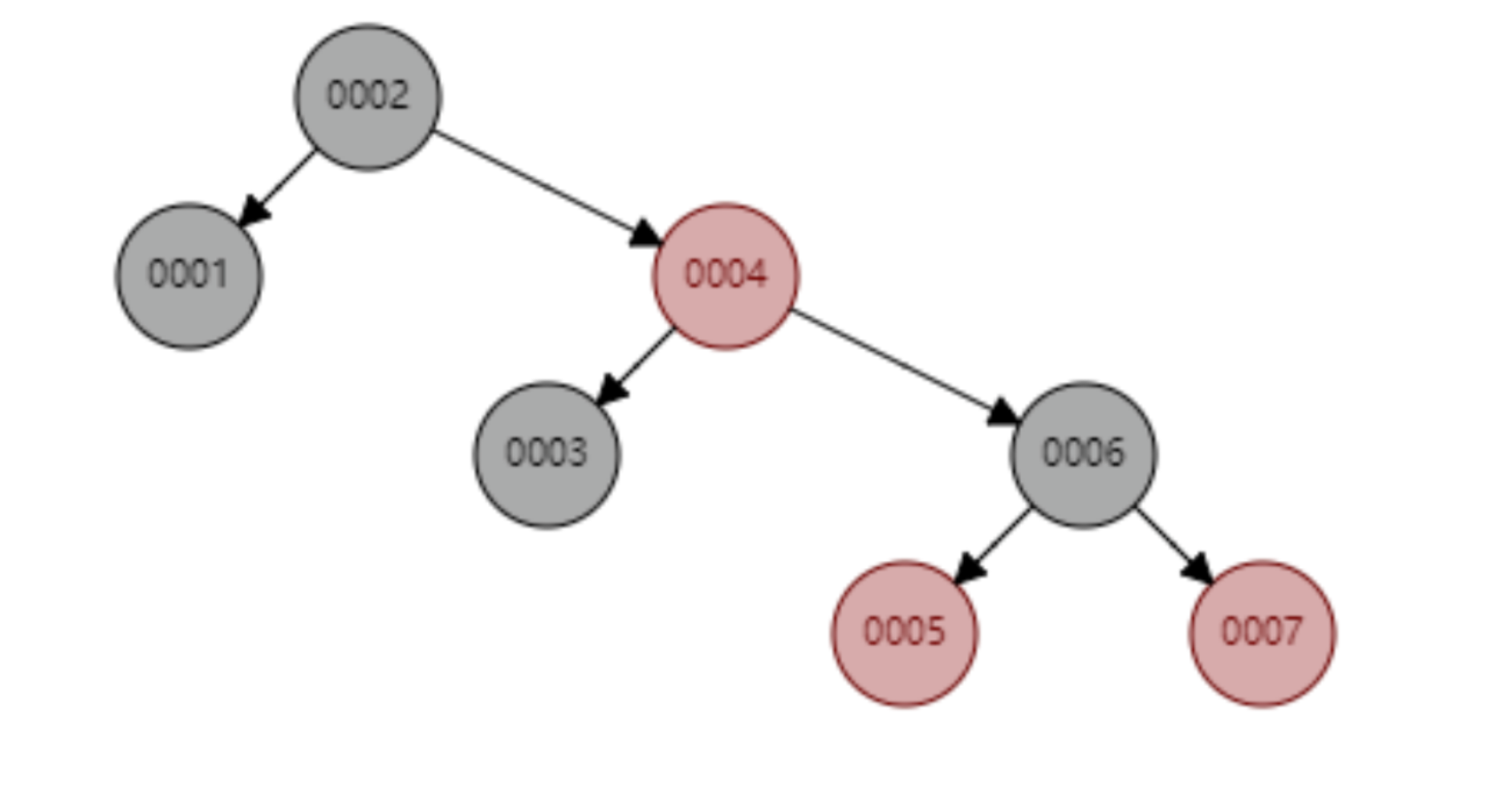
L'arbre rouge-noir insère séquentiellement 1 à 16 nœuds, et le nombre de nœuds qui doivent être comparés pour trouver l'identifiant = 16 est 6 fois. Observez la forme de cet arbre. Est-il vrai que lorsque les données sont insérées de manière séquentielle, la forme de l'arbre a toujours été dans une tendance « à droite » ? Fondamentalement, l'arbre rouge-noir ne résout pas complètement l'arbre de recherche binaire. Bien que cette tendance « à droite » soit beaucoup moins exagérée que l'arbre de recherche binaire dégénérant en une liste chaînée linéaire, l'opération de base d'auto-incrémentation de clé primaire dans le base de données, la clé primaire est généralement des millions et des dizaines de millions. Si l'arbre rouge-noir a ce genre de problème, cela consommera également énormément de performances de recherche. Notre base de données ne peut pas tolérer ce genre d'attente inutile.
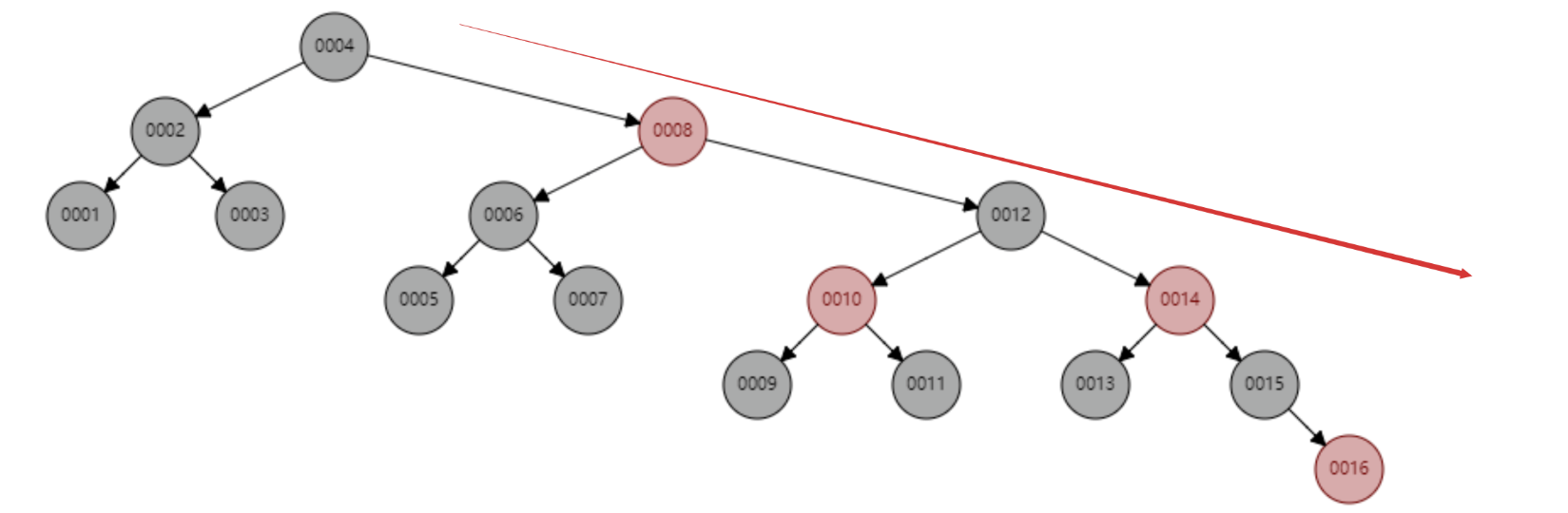
Considérons maintenant un autre arbre binaire à auto-équilibrage plus strict, l'arbre AVL. Étant donné que l'arbre AVL est un arbre binaire absolument équilibré, il consomme plus de performances pour ajuster la forme de l'arbre binaire.
L'arbre AVL insère 1 à 7 nœuds séquentiellement, et le nombre de fois où comparer les nœuds pour trouver l'identifiant = 7 est de 3.
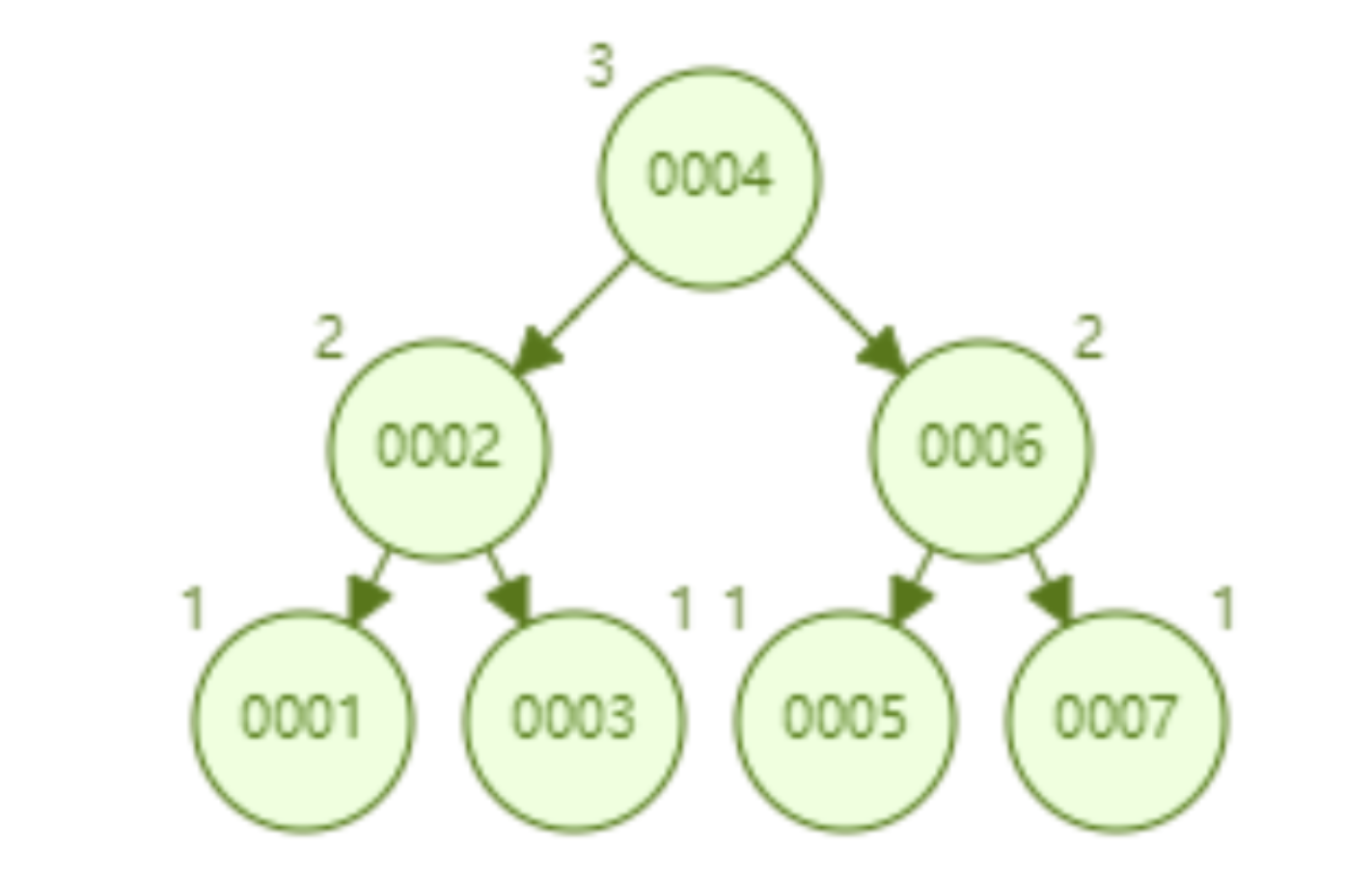
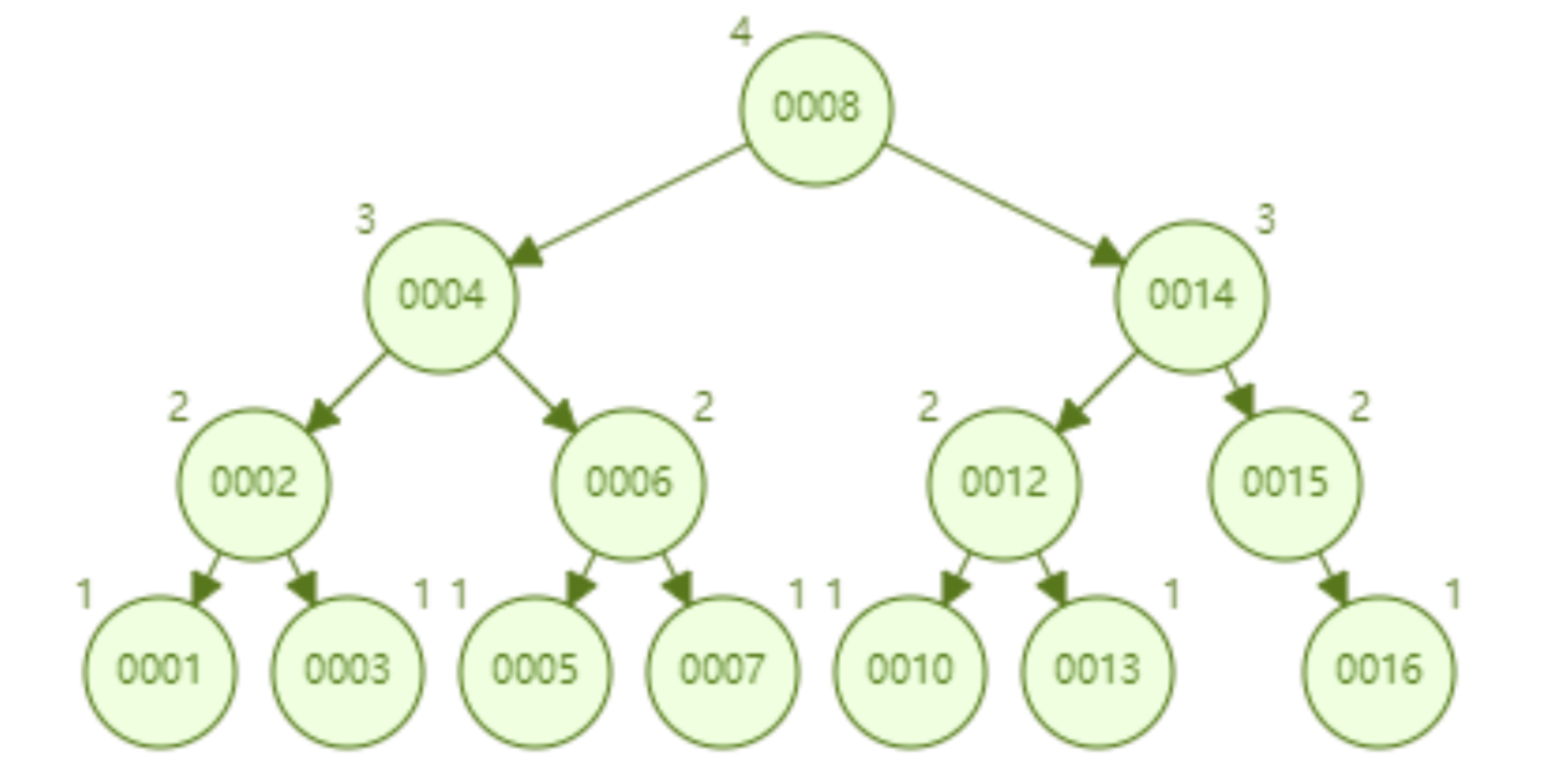
L'arbre AVL insère séquentiellement 1 à 16 nœuds, et le nombre de nœuds qui doivent être comparés pour trouver l'identifiant = 16 est de 4. En termes d'efficacité de recherche, la vitesse de recherche de l'arbre AVL est supérieure à celle de l'arbre rouge-noir (l'arbre AVL est de 4 comparaisons, l'arbre rouge-noir est de 6 comparaisons). À en juger par la forme de l'arbre, les arbres AVL n'ont pas le problème de « bonne inclinaison » des arbres rouge-noir. En d'autres termes, un grand nombre d'insertions séquentielles n'entraînera pas de diminution des performances des requêtes, ce qui résout fondamentalement le problème des arbres rouge-noir.
Pour résumer les avantages de l'arbre AVL :
Il semble que l'arborescence AVL soit vraiment bonne comme structure de données pour la recherche de données, mais l'arborescence AVL ne convient pas à la structure de données d'index de la base de données Mysql, car considérez ce problème :
Le goulot d'étranglement de la requête de base de données les données sont des E/S de disque. Si nous utilisons un arbre AVL et que chaque nœud de l'arbre ne stocke qu'une seule donnée, nous ne pouvons extraire les données que sur un nœud et les charger en mémoire avec un E/S de disque. Par exemple, pour interroger les données. avec id=7, nous devons effectuer des E/S disque trois fois. Cela prend du temps. Par conséquent, lors de la conception d’index de base de données, nous devons d’abord réfléchir à la manière de réduire autant que possible le nombre d’E/S disque.
Une caractéristique des E/S du disque est que le temps nécessaire pour lire 1 Mo de données et 1 Ko de données à partir du disque est fondamentalement le même. Sur la base de cette idée, nous pouvons stocker autant de données que possible sur un nœud d'arborescence. Un disque IO se charge. plus de données dans la mémoire. C'est le principe de conception du B-tree et du B+-tree.
B-tree
Le B-tree ci-dessous est limité au stockage de jusqu'à deux clés par nœud. Si un nœud a plus de deux clés, il sera automatiquement divisé. Par exemple, le B-tree suivant stocke 7 données. Il vous suffit d'interroger deux nœuds pour connaître l'emplacement spécifique des données avec id=7. Autrement dit, vous pouvez interroger les données spécifiées avec deux E/S de disque, ce qui est mieux que. l'arborescence AVL.
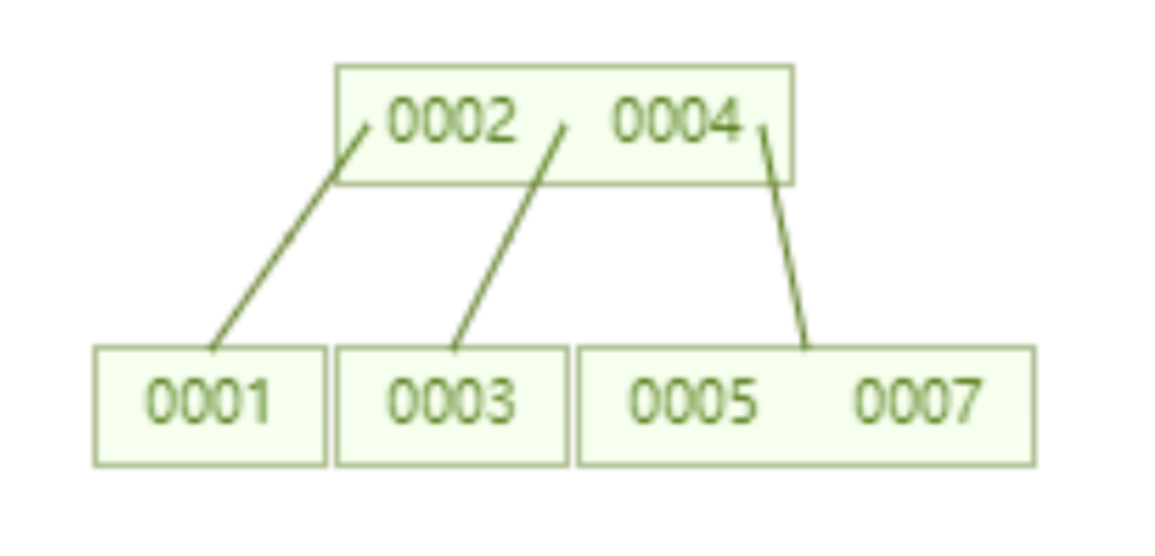
Ce qui suit est un arbre B qui stocke 16 éléments de données. De même, chaque nœud stocke jusqu'à 2 clés. L'interrogation des données avec id=16 nécessite d'interroger et de comparer 4 nœuds, ce qui signifie 4. le disque passe. On dirait que les performances des requêtes sont les mêmes que celles de l'arborescence AVL.
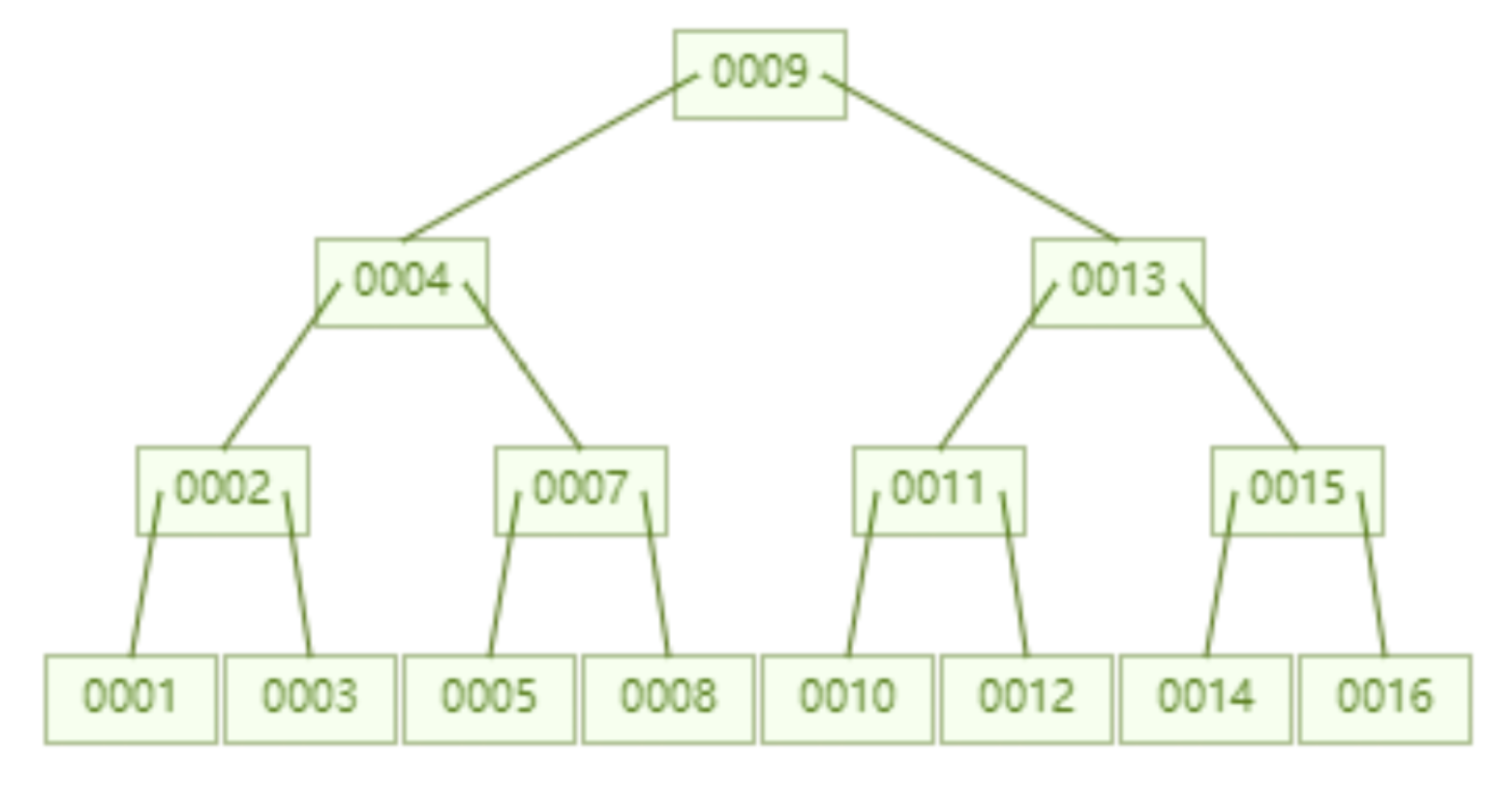
Mais étant donné que le temps consommé par les E/S du disque pour lire une donnée est fondamentalement le même que celui de la lecture de 100 données, alors notre idée d'optimisation peut être modifiée en : lire autant de données autant que possible dans une mémoire d'E/S de disque. Cela se reflète directement dans la structure de l'arborescence, c'est-à-dire que les clés que chaque nœud peut stocker peuvent être augmentées de manière appropriée.
Lorsque nous fixons à 6 le nombre de clés limitées à un seul nœud, pour un arbre B qui stocke 7 éléments de données, l'E/S disque requise pour interroger les données avec id=7 est de 2 fois.
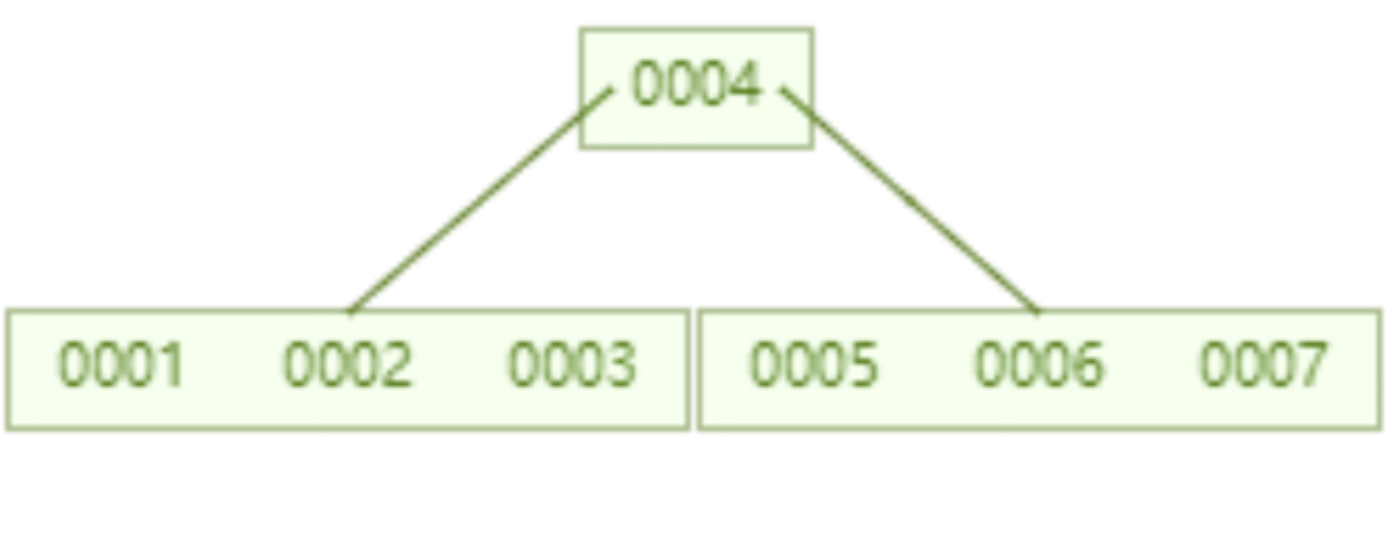
Un arbre B qui stocke 16 éléments de données. L'interrogation des données avec l'identifiant = 7 nécessite 2 E/S disque. Par rapport à l’arborescence AVL, le nombre d’E/S disque est réduit de moitié.

Donc, en termes de sélection de structure de données d'index de base de données, B-tree est un très bon choix. En résumé, le B-tree présente les avantages suivants lorsqu'il est utilisé comme index de base de données :
Quelle est la différence entre l'arbre B et l'arbre B+ ?
Premièrement, l'arbreB stocke les données dans un nœud, tandis que l'arbre B+ stocke les index (adresses), donc un nœud dans l'arbre B ne peut pas stocker beaucoup de données, mais un nœud dans l'arbre B+ peut stocker plusieurs index, arbre B+ les nœuds feuilles stockent toutes les données.
Deuxièmement, les nœuds feuilles de l'arbreB+ sont connectés en série à l'aide d'une liste chaînée au stade des données pour faciliter la recherche de plage.

En comparant l'arbre B et l'arbre B+, nous pouvons voir que les nœuds de l'arbre B+ stockent des index lorsque la capacité de stockage d'un seul nœud est limitée, un seul nœud peut également en stocker un grand nombre. d'index, ce qui rend l'ensemble B+. La hauteur de l'arborescence est réduite, ce qui réduit les E/S du disque. Deuxièmement, les nœuds feuilles de l'arborescence B+ sont l'endroit où les données réelles sont stockées. Les nœuds feuilles sont connectés à l'aide d'une liste chaînée. La liste chaînée elle-même est ordonnée et est plus efficace lors de la recherche dans la plage de données. Par conséquent, l'index de MySQL utilise l'arbre B+ et offre de très bonnes performances en termes d'efficacité de recherche et de recherche par plage.
Le moteur de données sous-jacent Mysql est conçu sous la forme de plug-ins. Les plus courants sont le moteur Innodb et le moteur Myisam. Les utilisateurs peuvent choisir différents moteurs en fonction de leurs besoins personnels. le moteur sous-jacent de la table de données Mysql. Nous venons d'analyser que l'arbre B+ est très approprié comme structure de données de l'index Mysql, mais la façon d'organiser les données et l'index nécessite également une certaine conception. La différence dans les concepts de conception a également conduit à l'émergence d'Innodb et de Myisam, chacun présentant des performances uniques. .
MyISAM Bien que les performances de recherche de données soient excellentes, elles ne prennent pas en charge le traitement des transactions. La plus grande caractéristique d'Innodb est qu'il prend en charge les fonctions de transaction compatibles ACID et qu'il prend en charge les verrous au niveau des lignes. Vous pouvez spécifier le moteur lorsque Mysql crée une table. Par exemple, dans l'exemple suivant, Myisam et Innodb sont spécifiés respectivement comme moteurs de données pour la table user et la table user2.

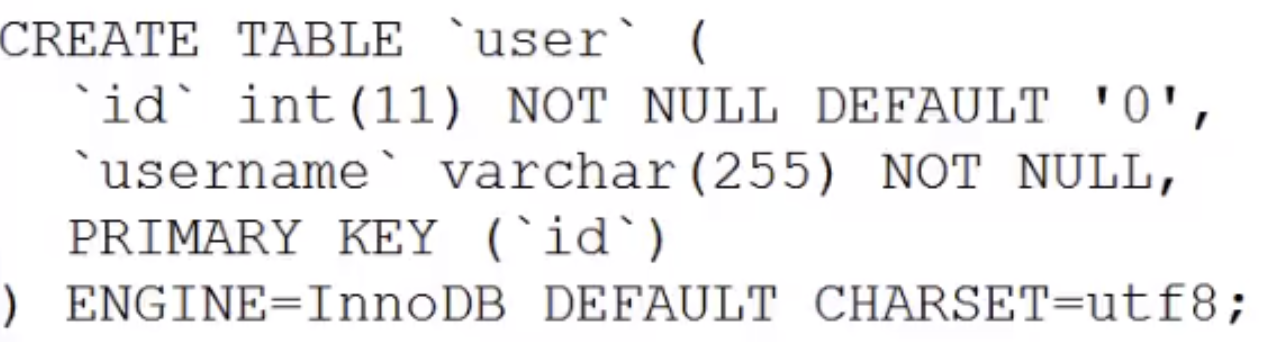
Après l'exécution de ces deux commandes, les fichiers suivants apparaissent dans le système, indiquant que les données et index des deux moteurs sont organisés différemment.
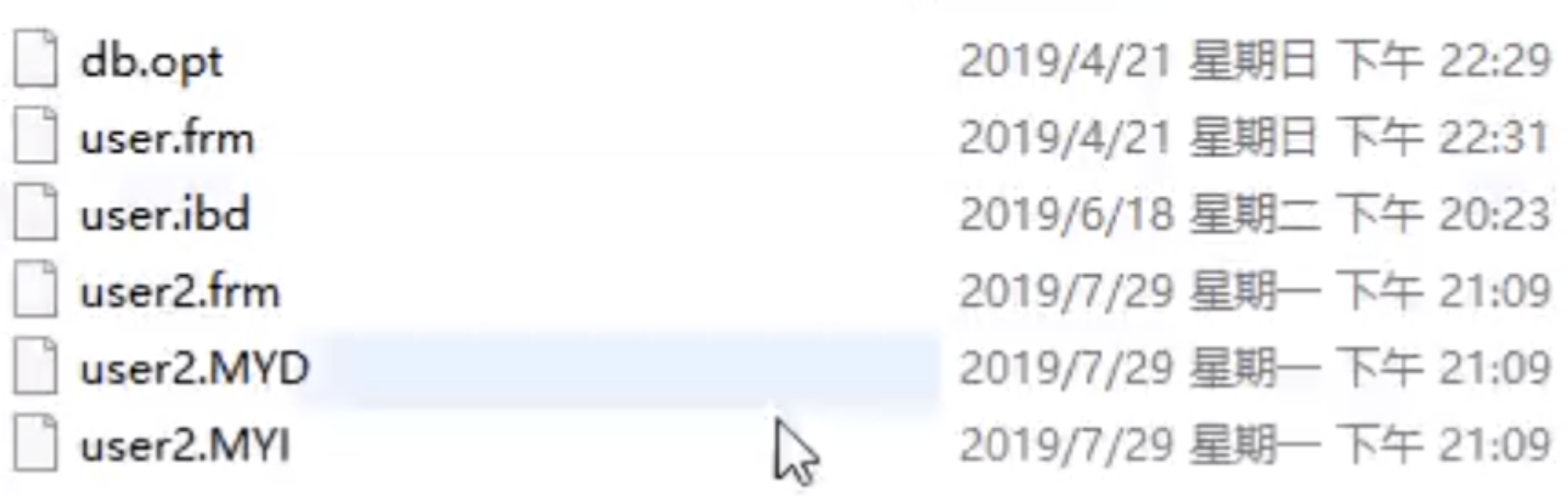
Les fichiers générés par Innodb après la création de la table sont :
Myisam généré après création de la table Les fichiers incluent
Jugement à partir du fichier généré, les données et index sous-jacents de ces deux moteurs sont organisés de différentes manières. Le moteur MyISAM sépare les données et l'index, chaque personne a un fichier, appelé méthode d'index non clusterisée ; données et index dans le même fichier. C'est ce qu'on appelle le mode index clusterisé. Ce qui suit analysera comment ces deux moteurs s'appuient sur la structure de données arborescente B+ pour organiser la mise en œuvre du moteur du point de vue de la mise en œuvre sous-jacente.
L'implémentation sous-jacente du moteur MyISAM (méthode d'index non clusterisée)
MyISAM utilise une méthode d'index non clusterisée, c'est-à-dire que les données et l'index tombent sur deux fichiers différents. Lorsque MyISAM crée une table, il utilise la clé primaire comme KEY pour créer une arborescence d'index primaire B+. Les nœuds feuilles de l'arborescence stockent l'adresse physique des données correspondantes. Après avoir obtenu cette adresse physique, nous pouvons localiser directement l'enregistrement de données spécifique dans le fichier de données MyISAM.
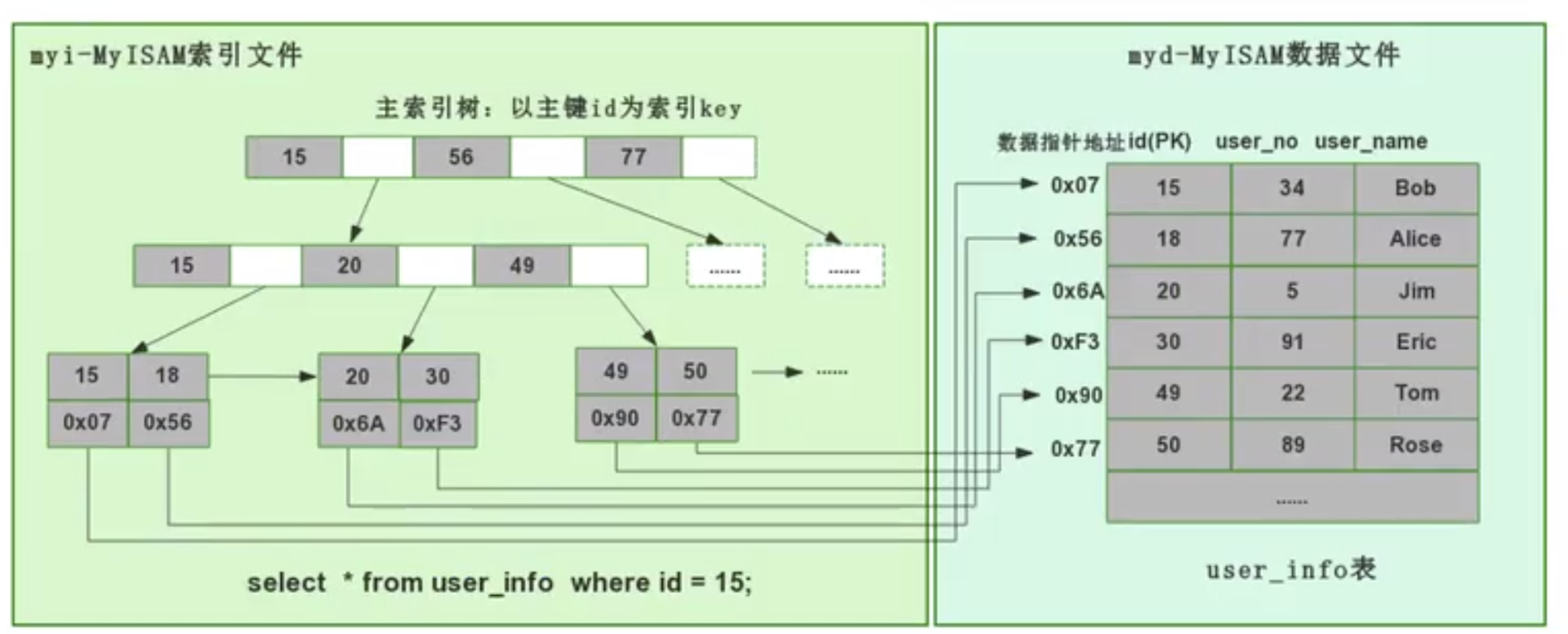
Lorsque nous ajoutons un index à un champ, nous générerons également un arbre d'index pour le champ correspondant. Les nœuds feuilles de l'arbre d'index pour le champ enregistrent également l'adresse physique des données correspondantes, puis prenez Utiliser cette adresse physique pour localiser l'enregistrement de données spécifique dans le fichier de données.
L'implémentation sous-jacente du moteur Innodb (méthode d'index clusterisé)
InnoDB est une méthode d'index clusterisé, donc les données et l'index sont stockés dans le même fichier. Tout d'abord, InnoDB construira un arbre d'index B+ basé sur l'ID de clé primaire comme KEY, comme le montre la figure ci-dessous, et les nœuds feuilles de l'arborescence B+ stockent les données correspondant à l'ID de clé primaire, par exemple, lors de l'exécution de l'instruction. select * from user_info où id=15, InnoDB Il interrogera l'arborescence B+ de l'index d'ID de clé primaire et trouvera le nom d'utilisateur correspondant='Bob'.
C'est à ce moment-là qu'InnoDB construira automatiquement l'arborescence d'index d'ID de clé primaire lors de la création d'une table. C'est pourquoi Mysql nécessite que la clé primaire soit spécifiée lors de la création d'une table. Comment InnoDB construit-il un arbre d'index lorsque nous ajoutons un index à un champ de la table ? Par exemple, si nous voulons ajouter un index au champ user_name, alors InnoDB créera un arbre B+ d'index de nom d'utilisateur. La KEY de user_name est stockée dans le nœud et les données stockées dans les nœuds feuilles sont la clé primaire KEY. Notez que les feuilles stockent la clé primaire KEY ! Après avoir obtenu la clé primaire KEY, InnoDB ira à l'arborescence d'index de clé primaire pour trouver les données correspondantes en fonction de la clé primaire KEY qui vient d'être trouvée dans l'arborescence d'index de nom_utilisateur.
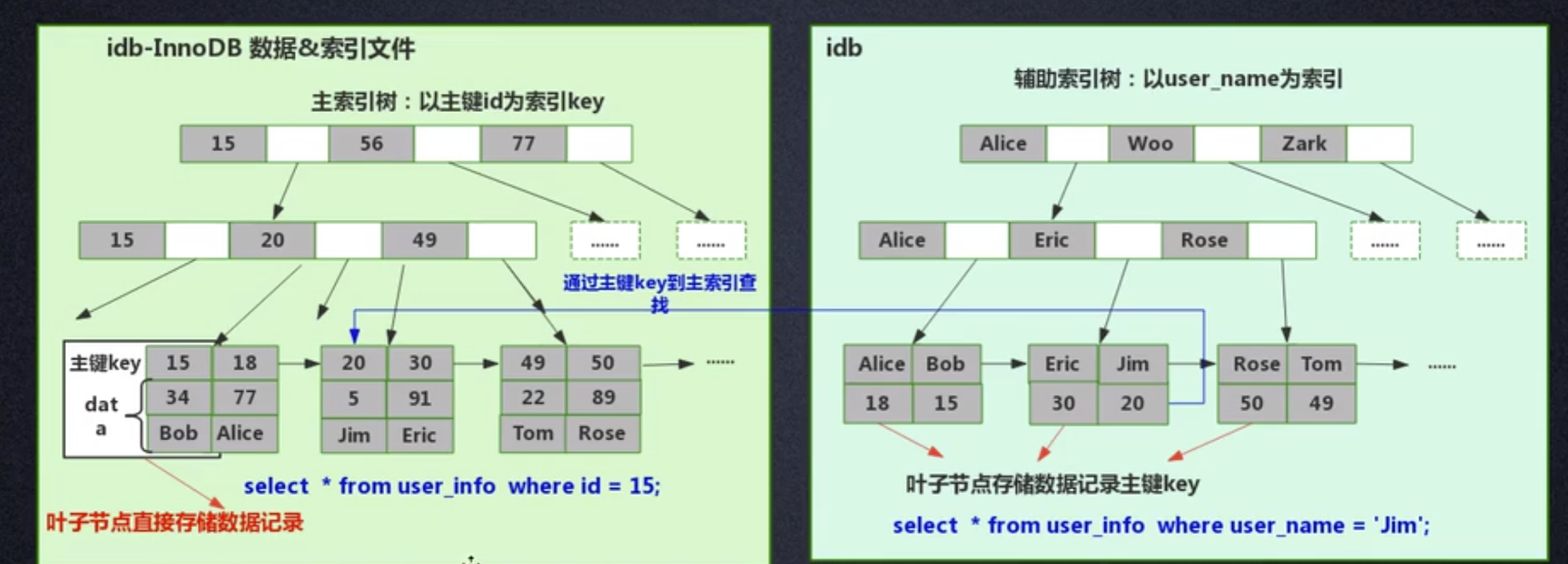
La question est de savoir pourquoi InnoDB stocke uniquement des données spécifiques dans les nœuds feuilles de l'arbre d'index de clé primaire, alors que les autres arbres d'index ne stockent pas de données spécifiques et qu'il n'est pas nécessaire de trouver d'abord la clé primaire. , puis dans l'arborescence d'index de clé primaire. Que diriez-vous de trouver les données correspondantes ?
C'est en fait très simple, car InnoDB a besoin d'économiser de l'espace de stockage. Il peut y avoir plusieurs index dans une table. InnoDB générera un arbre d'index pour chaque champ indexé. Si l'arbre d'index de chaque champ stocke des données spécifiques, alors le fichier de données d'index de cette table deviendra très volumineux (données extrêmement redondantes). Du point de vue de l'économie d'espace disque, il n'est vraiment pas nécessaire de stocker des données spécifiques dans chaque arborescence d'index de champ. Grâce à cette étape apparemment « inutile », un espace disque énorme est économisé au détriment des performances des requêtes.
Lors de la comparaison des fonctionnalités d'InnoDB et de MyISAM, il a été mentionné que MyISAM a de meilleures performances de requête. La raison peut également être vue dans la conception du fichier de données du fichier d'index ci-dessus : MyISAM peut localiser directement l'enregistrement de données après avoir directement trouvé le physique. adresse, mais après qu'InnoDB ait interrogé les nœuds feuilles, il doit à nouveau interroger l'arborescence d'index de clé primaire pour localiser les données spécifiques. Cela signifie que MyISAM peut trouver les données en une seule étape, mais InnoDB nécessite deux étapes. Bien entendu, les performances des requêtes de MyISAM sont plus élevées.
Cet article explique d'abord quelle structure de données est la plus adaptée à l'implémentation de l'index sous-jacent de MySQL, puis présente l'implémentation sous-jacente des deux moteurs de données classiques de MySQL, MyISAM et InnoDB. Enfin, résumons quand vous devez indexer les champs de votre table :
【Recommandations associées :tutoriel vidéo mysql】
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 mysql modifier le nom de la table de données
mysql modifier le nom de la table de données MySQL crée une procédure stockée
MySQL crée une procédure stockée La différence entre MongoDB et MySQL
La différence entre MongoDB et MySQL Comment vérifier si le mot de passe MySQL est oublié
Comment vérifier si le mot de passe MySQL est oublié mysql créer une base de données
mysql créer une base de données niveau d'isolement des transactions par défaut de MySQL
niveau d'isolement des transactions par défaut de MySQL La différence entre sqlserver et mysql
La différence entre sqlserver et mysql mysqlmot de passe oublié
mysqlmot de passe oublié