1. Aperçu de la distribution de probabilité
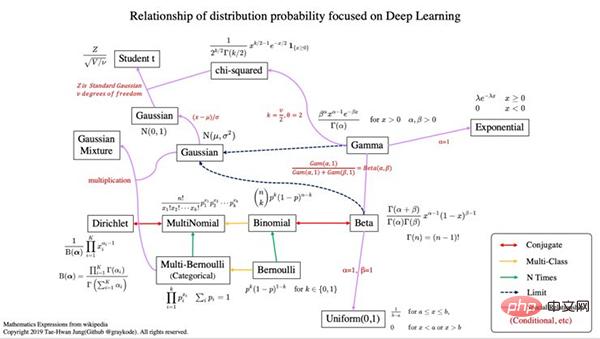
- Conjugué signifie qu'il a la relation d'une distribution conjuguée.
- Dans la théorie des probabilités bayésiennes, si la distribution a posteriori p(θx) et la distribution de probabilité a priori p(θ) sont dans la même famille de distribution de probabilité, alors l'a priori et l'a posteriori sont appelées distributions conjuguées, et l'a priori est appelée a priori conjugués pour fonctions de vraisemblance. Le conjugué Wikipédia antérieur est ici (https://en.wikipedia.org/wiki/Conjugate_prior).
- La classification multiple signifie que la variance aléatoire est supérieure à 2.
- n fois signifie que nous considérons également la probabilité a priori p(x).
- Pour en savoir plus sur les probabilités, je recommande de lire [reconnaissance de formes et apprentissage automatique, Bishop 2006].
2. Probabilité et caractéristiques de distribution
1. Distribution uniforme (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/uniform.py
La distribution uniforme a la même valeur de probabilité sur [a, b] et est une distribution de probabilité simple.
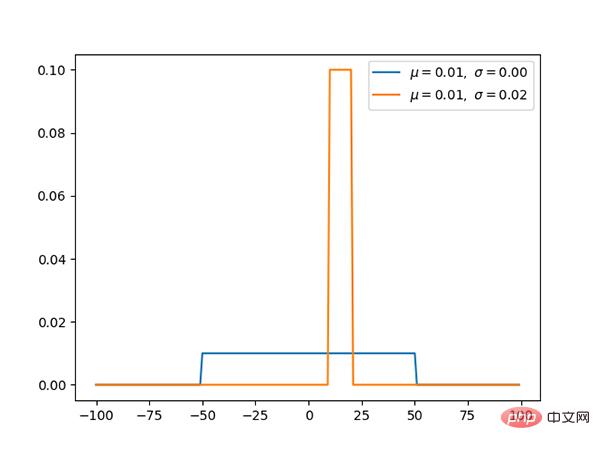
2. Distribution de Bernoulli (discrète)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/bernoulli.py
- Avant La probabilité p (x) ne prend pas en compte la distribution de Bernoulli. Par conséquent, si nous optimisons pour obtenir le maximum de vraisemblance, nous pouvons facilement devenir surajustés.
- Classification utilisant l'entropie croisée binaire pour la classification binomiale. Sa forme est la même que le logarithme négatif de la distribution de Bernoulli. Image
3. Distribution binomiale (discrète)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/binomial.py
- Les paramètres sont n et La distribution binomiale de p est une distribution de probabilité discrète du nombre de réussites dans une série de n expériences indépendantes.
- La distribution binomiale est une distribution qui prend en compte la probabilité a priori en précisant à l'avance la quantité à prélever.
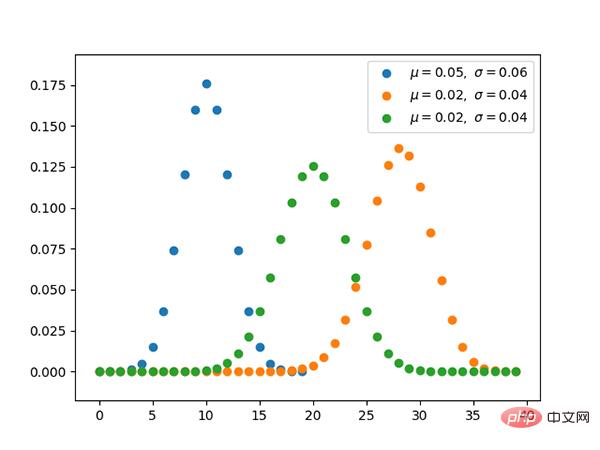
4. Distribution multi-Bernoulli, distribution catégorielle (discrète)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/categorical.py
- La distribution catégorique de Bernoulli multiple est appelée distribution catégorielle.
- L'entropie croisée a la même forme que la distribution multi-Bernoulli prenant le logarithme négatif.
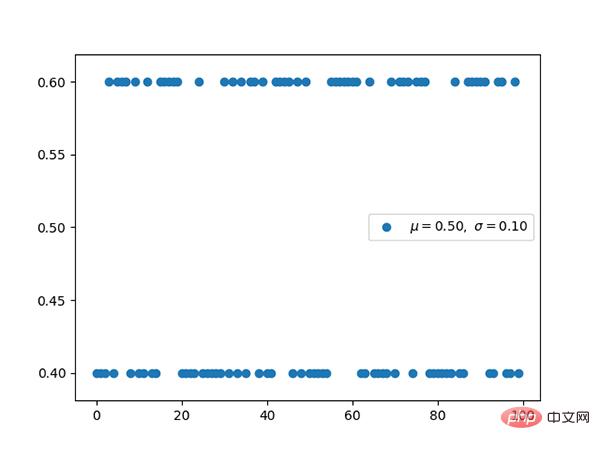
5. Distribution polynomiale (discrète)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/multinomial.py
Distribution et classification polynomiales La relation entre les distributions est la même que la relation entre la distribution de Bernoul et la distribution binomiale.
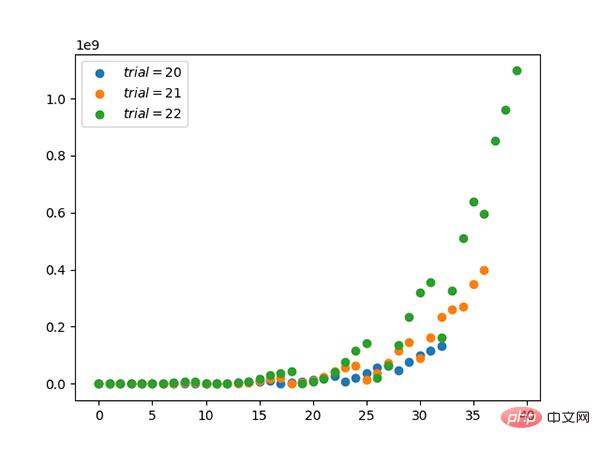
Distribution 6.β (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/beta.py
- β distribution et deux Le terme distribution est conjugué à la distribution de Bernoulli.
- En utilisant la conjugaison, la distribution a posteriori peut être obtenue plus facilement en utilisant la distribution a priori connue.
- Lorsque la distribution β satisfait le cas particulier (α=1, β=1), la distribution uniforme est la même.
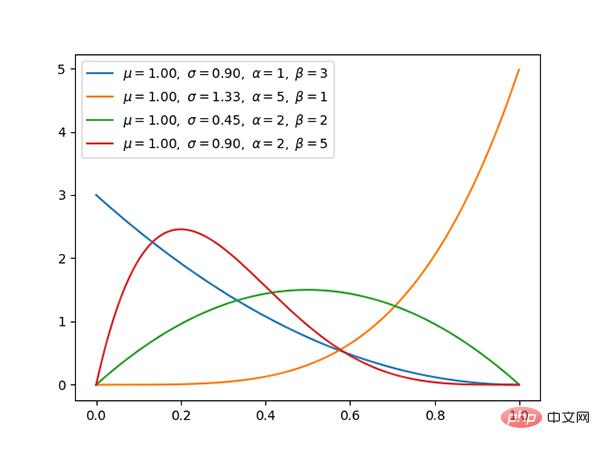
7. Distribution Dirichlet (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/dirichlet.py
- distribution dirichlet et Les distributions polynomiales sont conjuguées.
- Si k=2, c'est une distribution bêta.
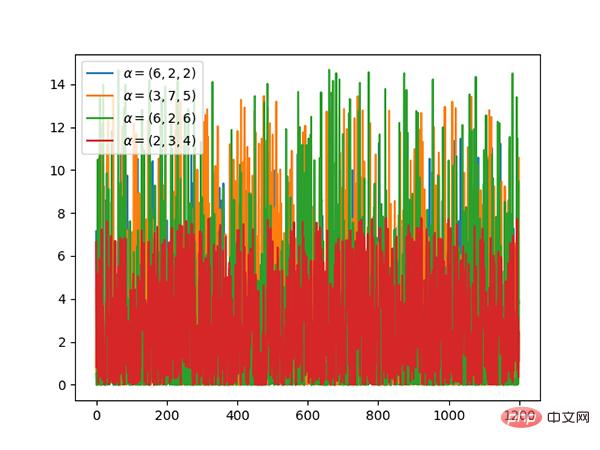
8. Distribution Gamma (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/gamma.py
- Si gamma ( a, 1)/gamma (a, 1) + gamma (b, 1) est identique à bêta (a, b), alors la distribution gamma est la distribution bêta.
- La distribution exponentielle et la distribution du chi carré sont des cas particuliers de la distribution gamma.
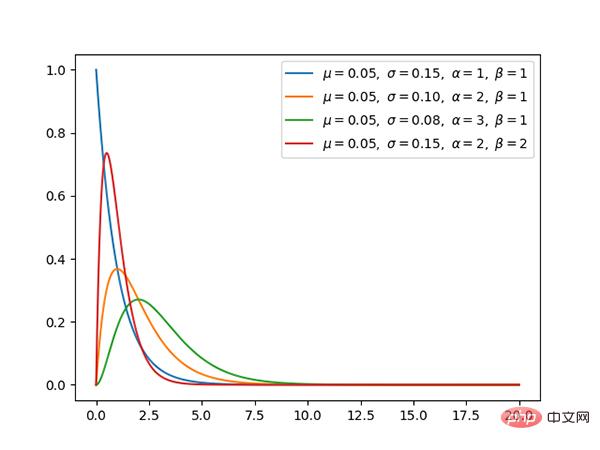
9. Distribution exponentielle (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/exponential.py
La distribution exponentielle est un cas particulier de la distribution γ lorsque α vaut 1.
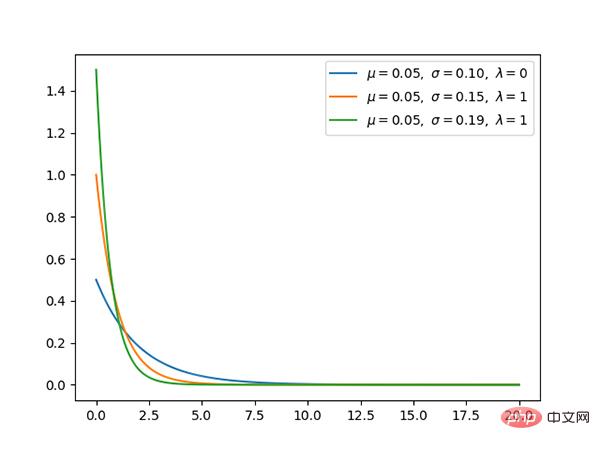
10. Distribution gaussienne (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/gaussian.py
La distribution gaussienne est une Distribution de probabilité continue très courante.
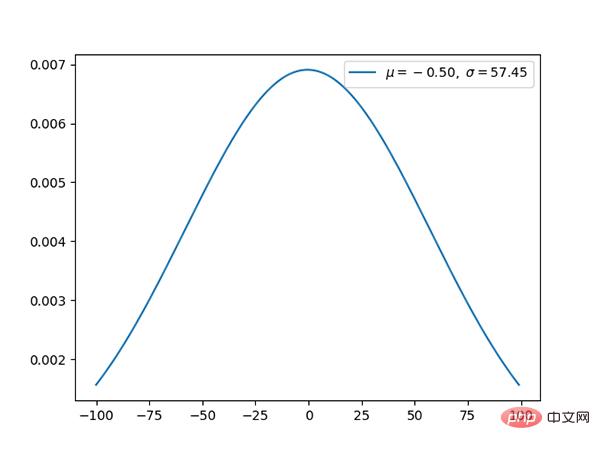
11. Distribution normale (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/normal.py
La distribution normale est La La distribution gaussienne standard a une moyenne de 0 et un écart type de 1.
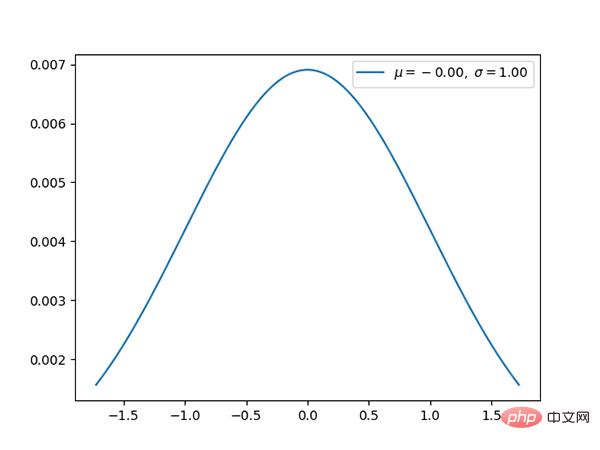
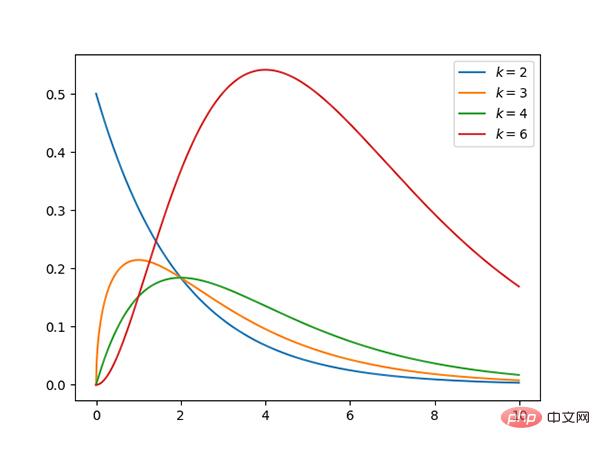
12. Distribution du Chi carré (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/blob/master/chi-squared.py
- k La distribution du Chi carré avec degrés de liberté est la distribution de la somme des carrés de k variables aléatoires normales standard indépendantes.
- La distribution du Chi carré est un cas particulier de distribution bêta
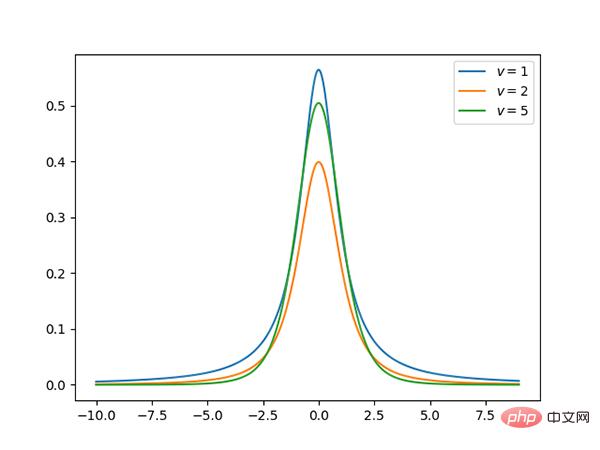
Distribution 13.t (continue)
Code : https://github.com/graykode/distribution-is-all-you-need/ blob/master /student-t.py
t La distribution est symétrique, en forme de cloche, similaire à la distribution normale, mais a des queues plus lourdes, ce qui signifie qu'elle est plus susceptible de produire des valeurs bien inférieures à la moyenne.
via : https://github.com/graykode/distribution-is-all-you-needa
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!














