

Introduction : Le titre de ce partage est "Comment mieux utiliser les données dans l'inférence causale ?" ", qui présente principalement les travaux récents de l'équipe liés aux articles publiés sur les causes et les effets. Ce rapport présente comment nous pouvons utiliser davantage de données pour faire des inférences causales sous deux aspects. L'un consiste à utiliser des données de contrôle historiques pour atténuer explicitement le biais de confusion, et l'autre est l'inférence causale dans le cadre de la fusion de données multi-sources.
Table des matières en texte intégral :
Les problèmes courants de prédiction d'apprentissage automatique sont généralement définis dans le même système, par exemple, une distribution indépendante et identique est généralement supposée, comme la prédiction de la probabilité de cancer du poumon chez les fumeurs. classification des images, etc. question. La question de la causalité concerne le mécanisme derrière les données. Des questions courantes telles que « Le tabagisme provoque-t-il le cancer du poumon ? » Des questions similaires sont des problèmes de causalité.
Il existe deux types de données très importants dans le problème de l'estimation de l'effet causal : un type est constitué de données d'observation et l'autre type est constitué de données expérimentales générées par des expériences contrôlées randomisées.

La principale différence entre le problème d'estimation causale E(Y|do(X)) et le problème traditionnel de prédiction ou de classification E(Y|X) est que : des conditions données se présentent. L'intervention proposée par Judy Pearl représente le symbole faire. Intervenez pour forcer la variable X à une certaine valeur. L'estimation des effets causals dans ce rapport fait principalement référence à l'estimation des effets causals à partir de données d'observation.
Comment mieux utiliser les données dans l'inférence causale ? Ce rapport présentera un tel sujet en utilisant comme exemples des articles récents publiés par deux équipes.
tree se compose principalement de deux modules :
Certains algorithmes d'arbre causal traditionnels Il est divisé en fonction de l'hétérogénéité des effets causals. L'idée de base est d'espérer que les effets causals du sous-nœud gauche et du sous-nœud droit après la division seront significativement différents, et l’hétérogénéité des effets causals des différentes distributions de données peut être capturée grâce au fractionnement.
Le critère de division de l'arbre causal traditionnel, tel que :
Une méthode courante d'estimation des paramètres consiste à soustraire directement le résultat moyen du groupe témoin du résultat moyen du groupe expérimental sur le nœud de feuille divisée comme estimation de l'effet causal. S'il s'agit d'une expérience contrôlée randomisée, le mécanisme d'attribution du traitement est aléatoire et la différence moyenne calculée à partir de celui-ci constitue l'effet causal. Le mécanisme d'allocation aléatoire garantit que la distribution des données du groupe expérimental et du groupe témoin est la même, ce que l'on appelle l'homogénéité.
Lorsqu'un nœud enfant est obtenu par fractionnement dans un arbre causal, peut-on garantir que la distribution du nœud enfant gauche et du nœud enfant droit obtenus par la scission est homogène ?
L'arbre causal traditionnel et l'arbre de soulèvement ne peuvent pas garantir que la distribution des nœuds enfants gauche et droit après la division est homogène. Par conséquent, l’estimation traditionnelle 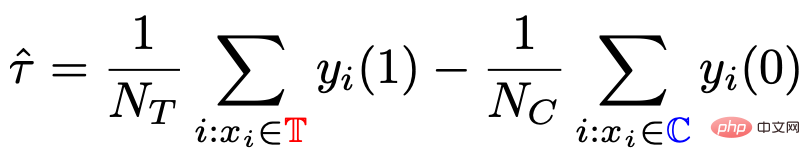 évoquée dans la section précédente est biaisée.
évoquée dans la section précédente est biaisée.
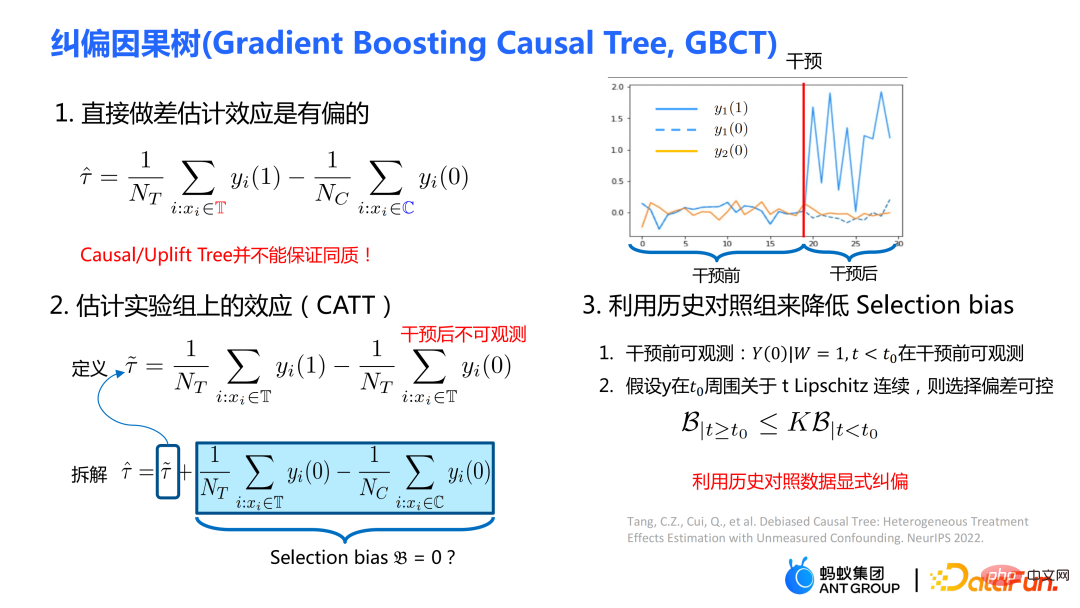
Notre travail se concentre sur l'estimation de l'effet causal moyen CATT sur le groupe expérimental (groupe de traitement). CATT est défini comme :
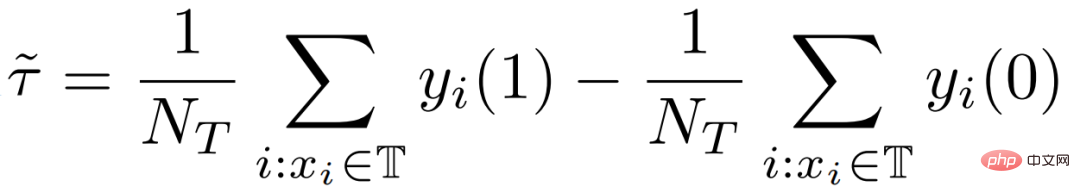
De plus, l'estimation traditionnelle de l'effet causal peut être divisée en deux parties :
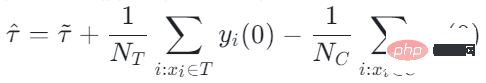
Le biais de sélection/biais de confusion peut être défini comme :
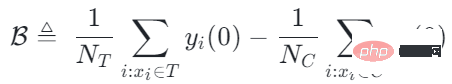
La signification intuitive est la valeur estimée lorsque le traitement = 0 dans le groupe expérimental, moins la valeur dans le groupe témoin Valeur estimée lorsque traitement=0. Dans les arbres causals traditionnels, le biais ci-dessus n'est pas caractérisé et le biais de sélection peut affecter nos estimations, entraînant un biais dans l'estimation finale.
Notre idée est d'utiliser les données de comparaison historiques accumulées sur le produit ou la plateforme pour réduire explicitement les biais de sélection. L'opération spécifique repose sur deux hypothèses :
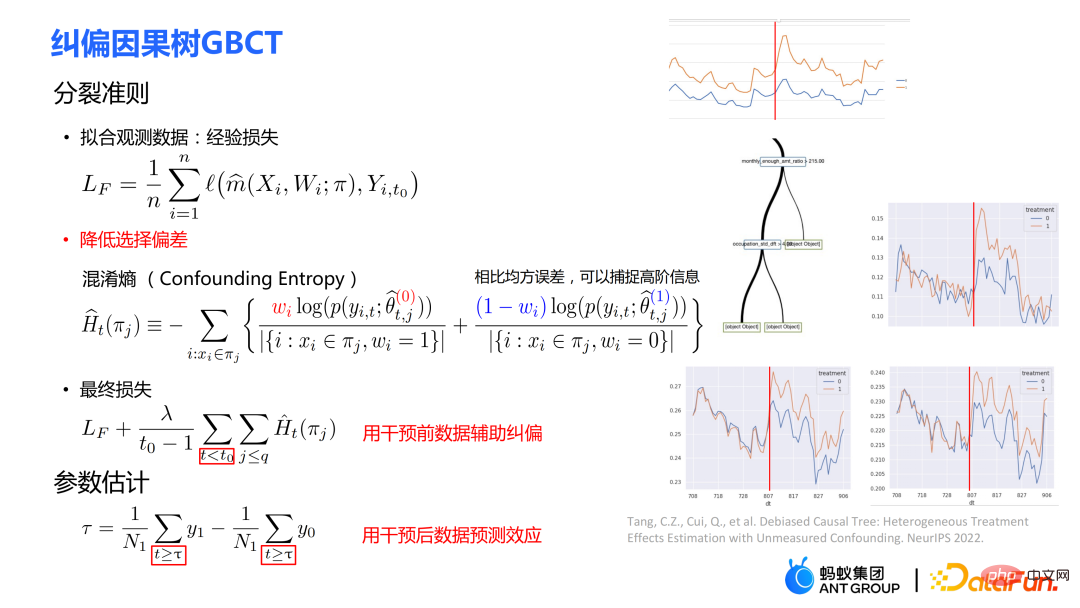
La méthode spécifique :
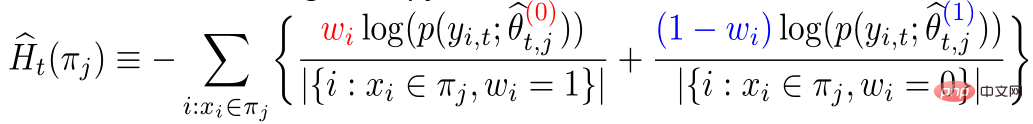
est : dans le groupe expérimental, utiliser le modèle du groupe témoin pour l'estimation ; dans le groupe témoin, utiliser le modèle du groupe expérimental pour l'estimation ; l'estimation de ces deux parties est aussi proche que possible, de sorte que la répartition du groupe expérimental et du groupe témoin soit aussi proche que possible. L'utilisation de l'entropie de confusion est l'une des principales contributions de nos travaux.
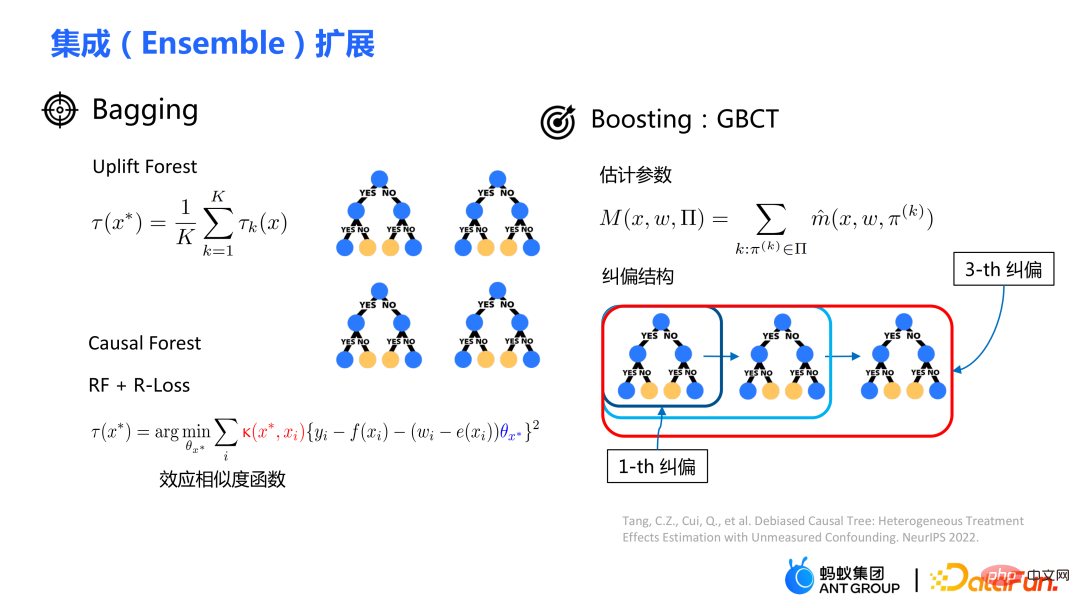
L'intégration de modèles d'arbres traditionnels comprend des méthodes telles que l'ensachage et le boosting. La méthode d'intégration utilisée par la forêt de soulèvement ou la forêt causale est la méthode d'ensachage. L'intégration de la forêt de soulèvement est une sommation directe, tandis que l'intégration de la forêt causale nécessite la résolution d'une fonction de perte.
Grâce au module de correction explicite conçu dans GBCT, GBCT prend en charge l'intégration à l'aide de la méthode boosting. L'idée de base est similaire au boosting : une fois le premier arbre corrigé, le deuxième arbre est corrigé, et le troisième arbre est corrigé...

Deux parties d'expériences ont été réalisées :
① Expérience de simulation. Dans le cadre d'expériences de simulation contenant une vérité terrain, testez si la méthode GBCT peut atteindre les résultats attendus. La génération de données pour l'expérience de simulation est divisée en deux parties (la première colonne Φ du tableau représente le biais de sélection. Plus la valeur Φ est grande, plus le biais de sélection correspondant est fort ; la valeur dans le tableau est MAE. Plus la valeur MAE est petite. , meilleure est la méthode) :
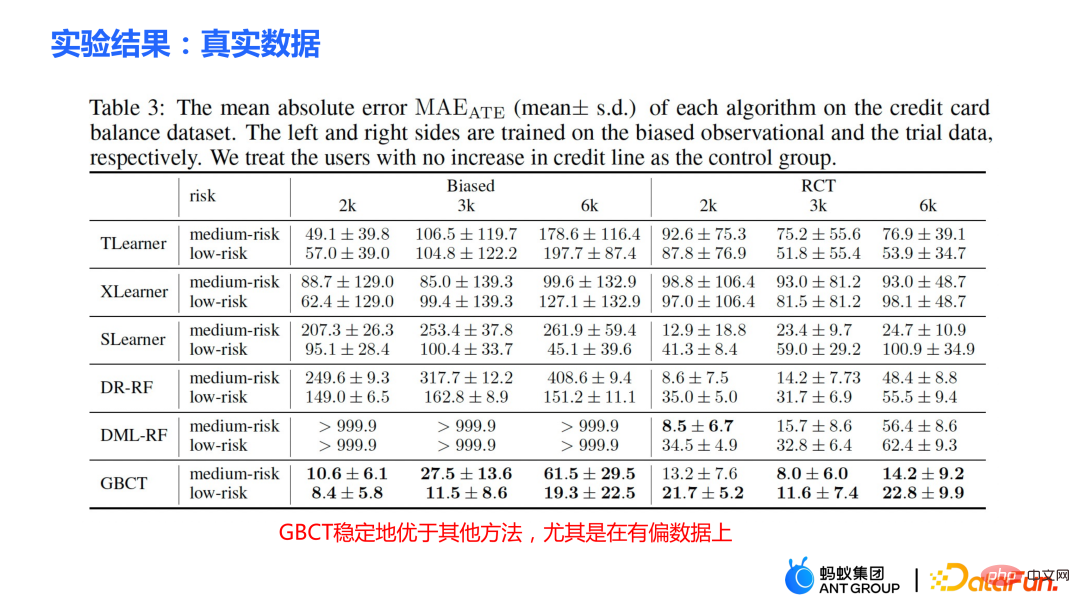
② Données d'augmentation de la limite de carte de crédit réelle. Une expérience contrôlée randomisée a été menée et des données biaisées ont été construites sur la base de l'expérience contrôlée randomisée. Dans différents contextes, la méthode GBCT surpasse systématiquement les méthodes traditionnelles, en particulier sur les données biaisées, avec des performances nettement meilleures que les méthodes traditionnelles.
Le deuxième travail est la fusion de données causales, c'est-à-dire comment mieux estimer l'effet causal lorsqu'il existe plusieurs sources de données.

Les symboles principaux : sont plusieurs sources de données, Y est le résultat, A est le traitement, X est la covariable d'intérêt, Z est les autres covariables de chaque source de données (domaine) sauf X Variable, S est l'indicateur du domaine utilisé pour indiquer à quel domaine il appartient, et μ est la valeur attendue du résultat potentiel. Décomposez le résultat dans l'expression suivante :
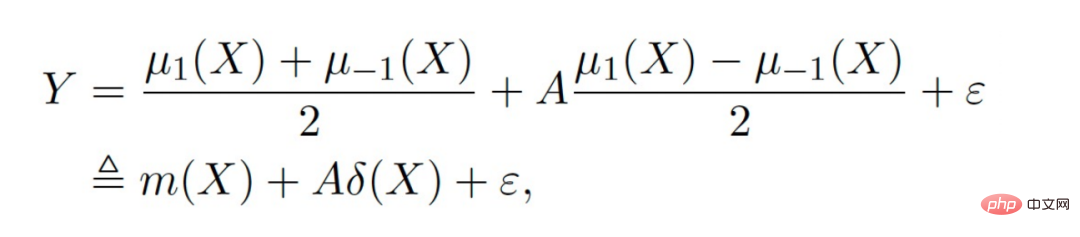
la fonction cible δ est utilisée pour estimer l'effet causal sur chaque domaine. De plus, les fonctions de nuisance incluent les effets principaux, les scores de propension, les scores de propension du domaine et la variance des effets. etc.
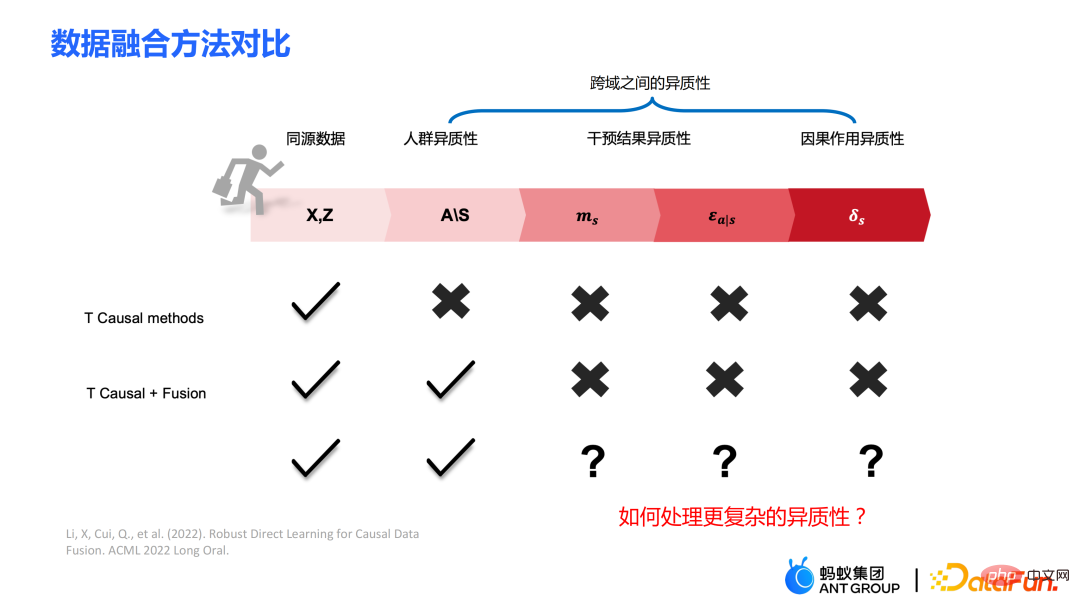
Certaines méthodes traditionnelles, comme le méta-apprenant, supposent que les données sont homologues, c'est-à-dire que la distribution est cohérente. Certaines méthodes traditionnelles de fusion de données peuvent gérer l’hétérogénéité des populations entre domaines, mais ne peuvent pas capturer explicitement l’hétérogénéité des résultats des interventions et des effets causals entre domaines. Notre travail se concentre sur le traitement d'une hétérogénéité plus complexe entre les domaines, y compris l'hétérogénéité entre les domaines dans les résultats des interventions et l'hétérogénéité entre les domaines dans les effets causals.
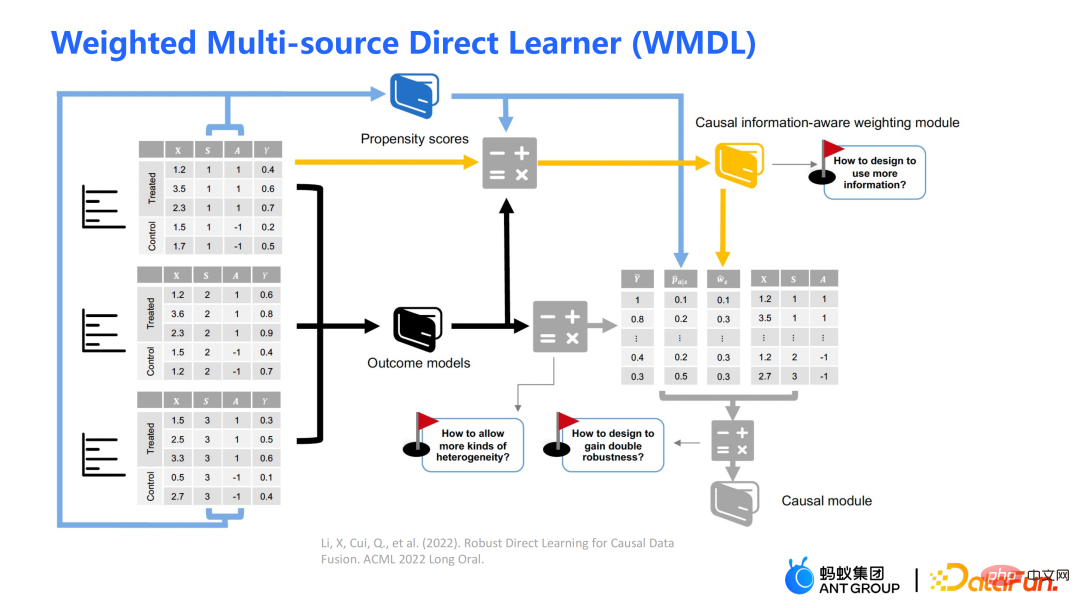
Le schéma-cadre de l'algorithme WMDL est présenté dans la figure ci-dessus. Les modules principaux sont :
obtenez le estimation. Les trois points forts de l'algorithme WMDL sont :
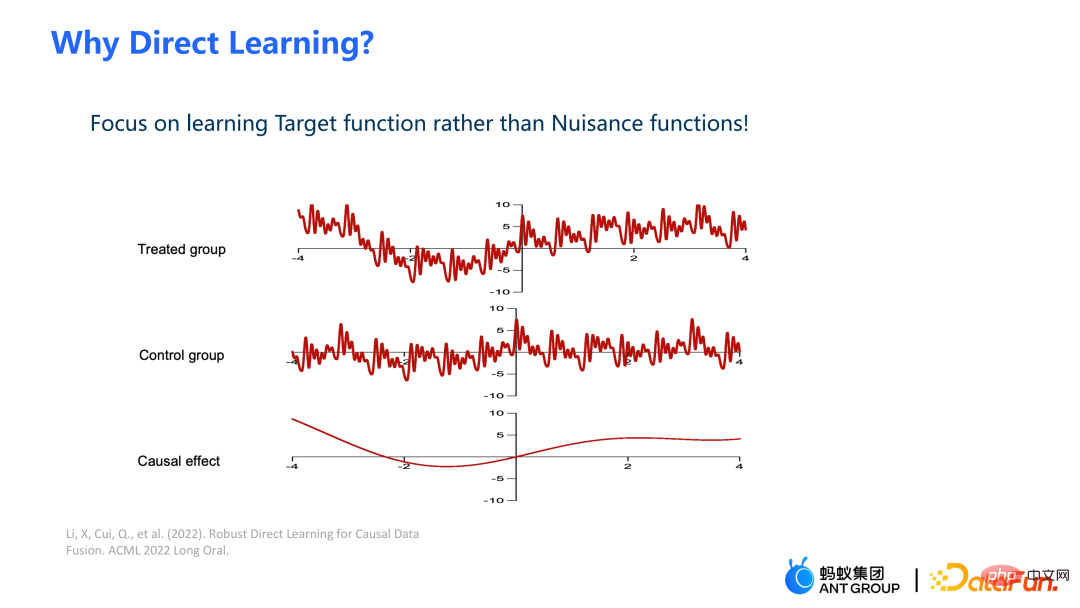
Dans ce travail, au lieu d'estimer le résultat du groupe expérimental et le résultat du groupe témoin, puis de faire une différence pour obtenir une estimation de l'effet causal, nous estimer directement l'effet causal, c'est-à-dire l'apprentissage direct. L’avantage de l’apprentissage direct est qu’il peut éviter les signaux de bruit à plus haute fréquence dans les groupes expérimentaux et témoins.

La partie de gauche suppose que les effets causals sont les mêmes dans plusieurs domaines, mais leurs résultats peuvent être hétérogènes ; Entre domaines, même si ses covariables sont les mêmes, leurs effets causals sont différents.
La formule est dérivée sur la base de la formule de démontage. Le résultat Y moins l'effet principal divisé par le traitement est estimé à I(X), et la solution optimale obtenue est δ(X). Le numérateur dans  est le module de pondération causale consciente de l'information qui sera mentionné plus tard, qui est une contribution majeure de notre travail ; le dénominateur est similaire au score de propension dans la méthode doublement robuste, mais il est également pris en compte dans ce domaine de travail. information. Si les effets causals entre différents domaines sont différents, les informations sur les indicateurs du domaine seront également prises en compte.
est le module de pondération causale consciente de l'information qui sera mentionné plus tard, qui est une contribution majeure de notre travail ; le dénominateur est similaire au score de propension dans la méthode doublement robuste, mais il est également pris en compte dans ce domaine de travail. information. Si les effets causals entre différents domaines sont différents, les informations sur les indicateurs du domaine seront également prises en compte.
Ce travail présente trois avantages :
① Grâce à différentes conceptions, il peut non seulement gérer l'hétérogénéité des résultats des interventions, mais aussi gérer l'hétérogénéité des effets causals
② Il a la propriété ; d'une double robustesse. La preuve est donnée dans l'article que tant que l'estimation du modèle de score de propension du domaine ou du modèle d'effet principal est impartiale, l'estimation finale sera impartiale (la situation réelle est un peu plus compliquée, voir l'article pour plus de détails)
③ Ce travail conçoit principalement le cadre du modèle semi-paramétrique. Chaque module du modèle peut utiliser n'importe quel modèle d'apprentissage automatique, et l'ensemble du modèle peut même être conçu dans un réseau neuronal pour réaliser un apprentissage de bout en bout. Le module de
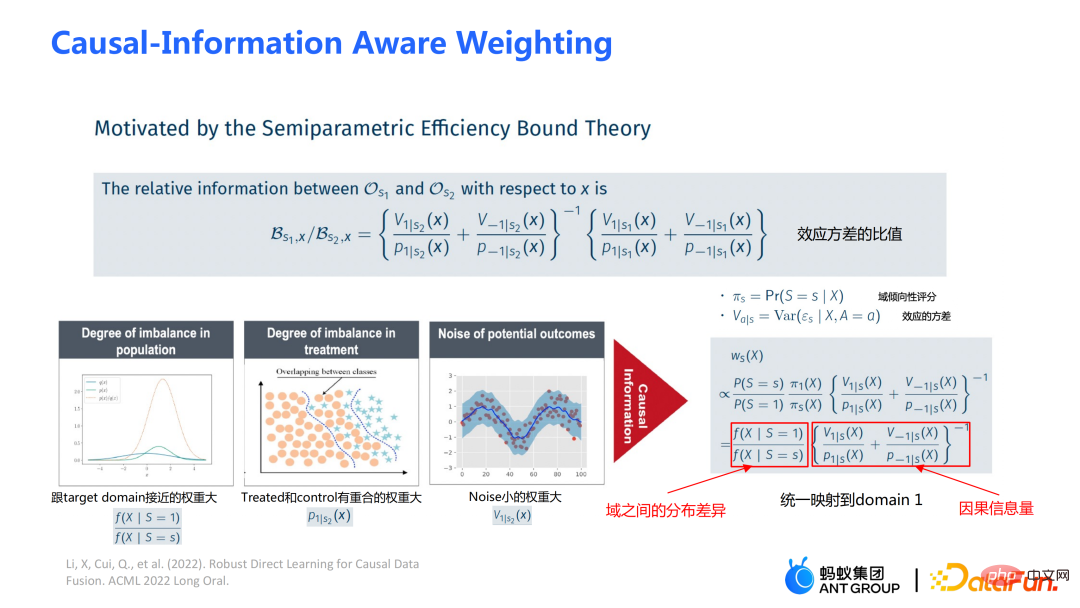
Poids est dérivé de la théorie liée à l'efficacité en statistique. Il contient principalement deux aspects d'informations :
① 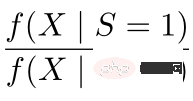 est un module de conversion équilibrée des différences de distribution entre les domaines ; Les trois images de gauche peuvent être utilisées pour faciliter la compréhension : Si la différence de distribution entre le domaine source et le domaine cible est importante, la priorité sera donnée aux échantillons les plus proches du domaine cible
est un module de conversion équilibrée des différences de distribution entre les domaines ; Les trois images de gauche peuvent être utilisées pour faciliter la compréhension : Si la différence de distribution entre le domaine source et le domaine cible est importante, la priorité sera donnée aux échantillons les plus proches du domaine cible 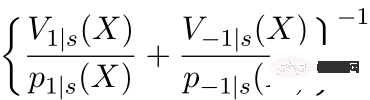 ; ② Grâce à la conception de la fonction de score de propension sur le dénominateur, un poids plus important est attribué aux échantillons qui se chevauchent dans le groupe expérimental et le groupe témoin
; ② Grâce à la conception de la fonction de score de propension sur le dénominateur, un poids plus important est attribué aux échantillons qui se chevauchent dans le groupe expérimental et le groupe témoin
③ Par V caractérise le bruit dans les données ; Puisque le bruit est au dénominateur, les échantillons avec moins de bruit auront des poids plus élevés.
En combinant intelligemment les trois parties ci-dessus, les différences de distribution entre différents domaines et les performances de différentes informations causales peuvent être cartographiées dans un domaine unifié.
Indépendamment des effets causals homogènes ou des effets causals hétérogènes, la méthode WMDL (Weighted Multi-domain Direct Learning) donne de meilleurs résultats. L'image de droite montre une expérience d'ablation sur le module de pondération. L'expérience montre l'efficacité du module de pondération. En résumé, la méthode WMDL est systématiquement plus performante que les autres méthodes et la variance estimée est relativement faible. 
4.Applications métiers dans Ant
Dans le scénario de contrôle du risque de crédit financier, les méthodes d'intervention telles que l'augmentation des quotas, la réduction des prix, etc. devraient obtenir l'effet attendu, comme des changements d'équilibre ou de risque. Dans certains scénarios réels, le travail de correction du GBCT utilisera les performances historiques de la période précédant le lifting du front (le statut du groupe expérimental et du groupe témoin sans lifting du front peut être obtenu) et effectuera une correction explicite grâce aux informations historiques, donc que l'intervention, les estimations ultérieures seront plus précises. Si le GBCT est divisé en un nœud enfant afin que les comportements pré-intervention soient alignés, les effets causals post-intervention seront plus faciles à estimer. (Obtenu après correction) Sur la figure, la couleur rouge correspond au groupe qui lève le front, la couleur bleue correspond au groupe sans élévation du front et la zone grise au milieu est l'effet causal estimé. GBCT nous aide à prendre de meilleures décisions intelligentes et à contrôler le solde et les risques des produits de crédit.
A1 : L'idée principale de la correction GBCT est d'utiliser les informations de contrôle historiques pour réduire explicitement le biais de sélection. La méthode GBCT et la méthode de double différence DID ont des similitudes et des différences :
A2 : Si toutes les variables confondantes ont été observées et répondent dans une certaine mesure à l'hypothèse d'ignorabilité, bien que le biais de sélection ne soit pas explicitement réduit, il est possible que le groupe expérimental et le groupe témoin soient séparés par les méthodes traditionnelles. Pour obtenir un alignement, les expériences montrent que le GBCT fonctionne légèrement mieux et que les résultats sont plus stables grâce à une correction explicite.
Supposons qu'il existe des variables confusionnelles non observées. Ce type de scénario est très courant dans la pratique. Il existe également des variables confusionnelles non observées dans les données de contrôle historiques, telles que la situation familiale et le revenu avant l'augmentation du quota. n'est pas observé, mais le comportement financier des utilisateurs a été reflété dans les données historiques. Nous espérons réduire explicitement le biais de sélection grâce à des méthodes telles que l'entropie de confusion grâce aux informations de performances historiques, de sorte que lorsque l'arbre est divisé, l'hétérogénéité entre les variables confondantes puisse être caractérisée dans les nœuds enfants divisés. Parmi les nœuds enfants, les variables confusionnelles non observées sont relativement proches, de sorte qu'elles ont une plus grande probabilité, de sorte que les effets causals estimés sont relativement plus précis.
A3 : J'ai fait une comparaison. Le Double Machine Learning est une méthode semi-paramétrique. Notre travail dans cet article se concentre davantage sur les méthodes basées sur les arbres, de sorte que les apprenants de base sélectionnés sont des méthodes liées aux arbres ou aux forêts. DML-RF dans le tableau est la version Double Machine Learning de Random Forest.
Par rapport au DML, le GBCT considère principalement comment utiliser les données de comparaison historiques. Dans la méthode comparative, le résultat historique sera traité directement comme une covariable, mais cette méthode de traitement ne fait évidemment pas bon usage de l’information.
A4 : Ce problème est un problème très essentiel sur la scène financière. Dans la promotion des recherches, la différence entre hors ligne et en ligne peut être partiellement surmontée grâce à l'apprentissage en ligne ou aux tests A/B. Dans les scénarios financiers, en raison de l'influence politique, il n'est pas facile de mener des expériences en ligne ; de plus, la période d'observation des performances est généralement plus longue. Par exemple, il faut au moins un mois pour observer les commentaires des utilisateurs sur les produits de crédit. Il est donc très difficile de résoudre parfaitement ce problème.
Nous adoptons généralement la méthode suivante : utiliser des données de test de différentes périodes (OOT) pour vérification lors de l'évaluation hors ligne et observer la robustesse de ses performances. Si les performances du test sont relativement stables, il y a alors relativement plus de raisons de croire que ses performances en ligne sont également bonnes.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 La différence entre le compte de service WeChat et le compte officiel
La différence entre le compte de service WeChat et le compte officiel
 Comment lire une vidéo avec python
Comment lire une vidéo avec python
 Ordre recommandé pour apprendre le langage C++ et C
Ordre recommandé pour apprendre le langage C++ et C
 Comment créer une page Web en python
Comment créer une page Web en python
 Supprimer l'historique de recherche
Supprimer l'historique de recherche
 Quels sont les systèmes d'exploitation mobiles ?
Quels sont les systèmes d'exploitation mobiles ?
 shib coin dernières nouvelles
shib coin dernières nouvelles
 numéro de série cad2012 et collection de clés
numéro de série cad2012 et collection de clés