Tri des échanges : L'idée de base du tri des échanges est de comparer les valeurs clés de deux enregistrements. Si les valeurs clés des deux enregistrements sont dans l'ordre inverse, échangez les deux enregistrements, afin que l'enregistrement soit obtenu. avec la valeur de clé la plus petite est déplacé dans la direction opposée vers l'avant de la séquence et les enregistrements avec des valeurs de clé plus grandes se déplacent vers l'arrière de la séquence.
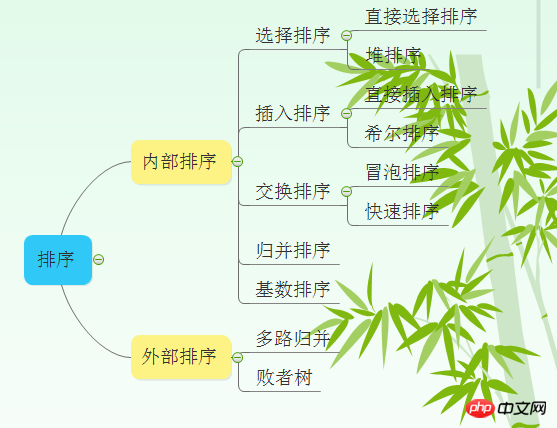
1. Tri à bulles
Introduction :
Tri à bulles (Tri à bulles, traduit de Taiwan par : Tri à bulles ou tri à bulles) est un simple algorithme de tri . Il parcourt à plusieurs reprises la séquence à trier, en comparant deux éléments à la fois et en les échangeant s'ils sont dans le mauvais ordre. Le travail de visite du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié. Le nom de cet algorithme vient du fait que les éléments plus petits « flotteront » lentement vers le haut du tableau grâce à l’échange.
Étapes :
Comparez les éléments adjacents. Si le premier est plus grand que le second, échangez-les tous les deux.
Faites de même pour chaque paire d'éléments adjacents, de la première paire du début à la dernière paire à la fin. À ce stade, le dernier élément doit être le plus grand nombre.
Répétez les étapes ci-dessus pour tous les éléments sauf le dernier.
Continuez à répéter les étapes ci-dessus pour de moins en moins d'éléments à chaque fois jusqu'à ce qu'il n'y ait plus de paires de nombres à comparer.
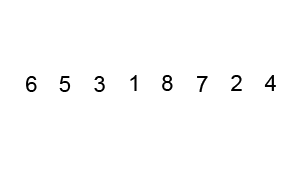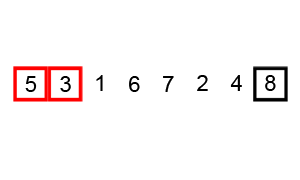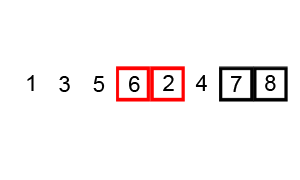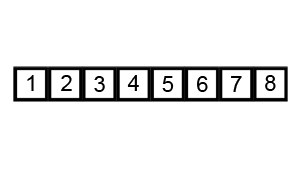
Le tri à bulles est le plus simple à comprendre, mais la complexité temporelle est ( O(n^2)) est également l'un des plus grands. Le code d'implémentation est le suivant :
.<br/>
$arr=tableau(1,43,54,62,21 ,66,32,78,36,76,39); $arr
){
$lencount
(); //Définir un tableau vide pour recevoir les bulles qui apparaissent
//Cette boucle de calque contrôle le nombre de tours qui doivent bouillonner
pour($i
=1;<$len;$i++) { //Cette couche de boucle est utilisée pour contrôler le nombre de fois qu'un nombre doit être comparé à chaque tour
pour(k$=0;k$<$len-$i;$k ++)
{
si ($arr[$k]>$arr [k$+1])
{
$tmp=$arr[$k +1] ;
$arr[$k+1] =$arr[$k];
$arr[$k]=$tmp; 🎜>
$ arr
} >2. 🎜>Introduction : Le tri rapide a été développé par Tony HallUn algorithme de tri développé. Dans des circonstances moyennes, le tri de n éléments nécessite des comparaisons
Οlog n). Dans le pire des cas, des comparaisons
Ο2) sont nécessaires, mais cette situation est rare. En fait, le tri rapide est généralement beaucoup plus rapide que les autres algorithmes Ο(n log
n) car sa boucle interne peut être utilisée dans la plupart des cas. L'architecture est implémentée de manière très efficacement, et dans la plupart des données du monde réel, la possibilité d'un terme quadratique peut déterminer les choix de conception et réduire le temps requis.
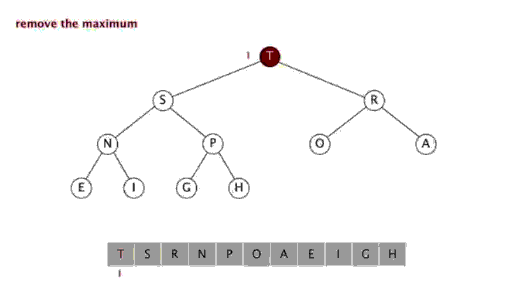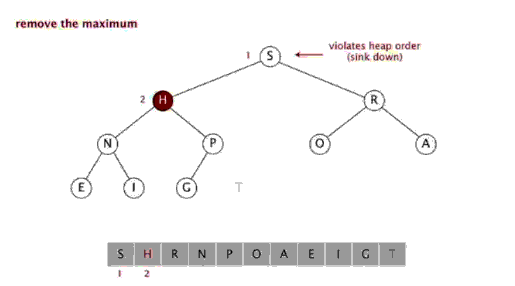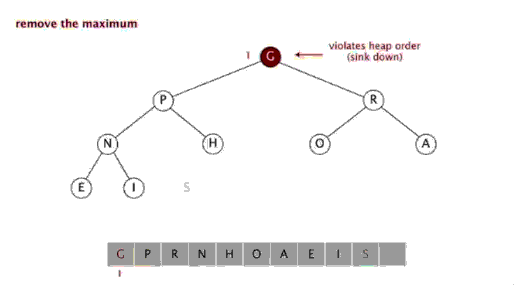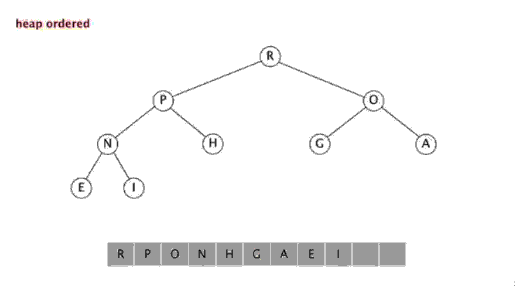
Étapes : Sélectionnez un élément de la séquence, appelé le "pivot", Réorganisez la séquence, tous les éléments plus petits que la valeur de base sont placés devant la base, et tous les éléments plus grands que la valeur de base sont placés derrière la base (le même nombre peut aller des deux côtés). Une fois cette partition terminée, la base se trouve au milieu de la séquence. C'est ce qu'on appelle l'opération partition . Récursivement trier le sous-tableau d'éléments plus petits que la valeur de base et le sous-tableau d'éléments supérieurs à la valeur de base. Le tri rapide est également un algorithme de tri efficace, et sa complexité temporelle est également O( nlogn). Le code est le suivant : function quick_sort($arr ) { //Déterminez d'abord si vous devez continuer $longueur = compte($arr); ) { retour $arr; } 🎜> //Sélectionnez une règle //Sélectionnez le premier élément $base_num = $arr [0]; //Parcourez tous les éléments sauf la règle et placez-les dans deux tableaux en fonction de leur taille //Initialiser deux tableaux $left_array = array();// plus petit que la règle $right_array = array ();// supérieur au souverain pour($i=1; $i<$longueur; $i++) { if($base_num > $arr[$i]) { 🎜> $left_array[] = $arr[$i]; { $right_array[] = $arr[$i]; > //Puis effectuer le même processus de tri sur les tableaux de gauche et de droite respectivement //Appeler cette fonction de manière récursive et enregistrer le résultat $left_array ); $right_array ); //Fusionner la règle de gauche et la droite return array_merge($left_array , tableau($base_num), $right_array ); } Sélectionner le tri Le tri par sélection comprend deux types, à savoir le tri par sélection directe et le tri par tas. L'idée de base du tri par sélection est qu'à chaque fois n-. i+ Sélectionnez l'enregistrement avec la plus petite valeur de clé parmi 1 (i=1,2,3,...,n-1) enregistrements comme i-ème enregistrement dans la séquence ordonnée 3. Tri par sélection Introduction : Le tri par sélection est un algorithme de tri simple et intuitif. Voici comment cela fonctionne. Tout d'abord, recherchez le plus petit élément de la séquence non triée et stockez-le au début de la séquence triée. Ensuite, continuez à rechercher le plus petit élément parmi les éléments non triés restants, puis placez-le à la fin de la séquence triée. Et ainsi de suite jusqu'à ce que tous les éléments soient triés. Le tri de sélection est également relativement simple à comprendre, et la complexité temporelle est également O(n^2). [php] voir en clair copier <br/> fonction select_sort($arr) { //Idée de mise en œuvre : la double boucle est terminée, la couche externe contrôle le nombre de tours et la valeur minimale actuelle. Le nombre de comparaisons contrôlées par la couche interne //$i La position de la valeur minimale actuelle , qui doit participer à la comparaison Éléments =0, $len =compte($arr) $i<🎜 ; ><$len-1; $i++ ) { = $i <🎜; > //À quels éléments $j doit-il actuellement être comparé, ceux après $i. pour($j=$i+1; $j<$len<🎜 ++) { <; 🎜> 🎜> si($arr $p] > $arr[$j ]) { > //Comparez, trouvez le plus petit, enregistrez la position de la valeur minimale et dans la comparaison suivante, // La valeur minimale connue doit être utilisée à des fins de comparaison. <; 🎜> } 🎜 > //La position de valeur minimale actuelle a été déterminée et enregistrée dans $p. //Si la position de la valeur minimale s'avère différente de la position actuelle supposée $ i, les positions s'excluent mutuellement. Il suffit de changer 🎜> != $ i) { 🎜> = [$p]; $arr[ ] = $arr [$i] $i <; 🎜> //Retour au résultat final retour $arr } 4. Tri par tas <br/> heap. Le tas est une structure complète d'arbre binaire approximative, et satisfait simultanément la propriété du tas : c'est-à-dire, les nœuds enfants Une clé ou un index est toujours plus petit (ou plus grand) que son nœud parent. Le tri par tas fait référence à un algorithme de tri conçu à l'aide d'une structure de données telle qu'un arbre empilé (tas), utiliser les caractéristiques des tableaux pour localiser rapidement l'élément à l'index spécifié. Le tas est divisé en un grand tas de racines et un petit tas de racines, qui est un arbre binaire complet. L'exigence d'un grand tas racine est que la valeur de chaque nœud ne soit pas supérieure à la valeur de son nœud parent, c'est-à-dire A[PARENT[i]] >= A[i]. Dans le tri non décroissant d'un tableau, un grand tas racine doit être utilisé, car selon les exigences d'un grand tas racine, la plus grande valeur doit être en haut du tas. 堆排序是一种高效的排序算法，它的时间复杂度是O(nlogn)。原理是：先把数组转为一个最大堆，然后把第一个元素跟第i元素交换，然后把剩下的i-1个元素转为最大堆，然后再把第一个元素与第i-1个元素交换，以此类推。实现代码如下： <br/> <br/> 插入排序 五、插入排序 介绍： 插入排序（Insertion Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。 步骤： 从第一个元素开始，该元素可以认为已经被排序 取出下一个元素，在已经排序的元素序列中从后向前扫描 如果该元素（已排序）大于新元素，将该元素移到下一位置 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置 将新元素插入到该位置中 重复步骤2 [php] voir en clair copier <br/> fonction insert_sort($arr) { //Distinguer quelle pièce a été triée / /Quelle la pièce n'est pas triée //Trouver un des éléments à trier //Cet élément commence à partir du deuxième élément et se termine par le dernier élément à trier //Utilisez une boucle pour le baliser //i loop contrôle les éléments qui doivent être insérés à chaque fois. Une fois les éléments qui doivent être insérés sont contrôlés, <. 🎜> //Indirectement le tableau a été divisé en 2 parties, l'indice est plus petit que celui actuel (celui de gauche), c'est la séquence triée pour($i=1, $len=compte($arr $i<); ;$len; $i++) { //Obtenir la valeur actuelle de l'élément qui doit être comparée. [$i] Comparez et insérez 🎜> = $j>=0;$j --) { //$arr[$i];//Éléments à insérer $arr[$j];//Éléments à comparer >$arr[$j]) { Les éléments sont inter modifié avec les éléments précédents 🎜>$j+1] = $arr $j ]; $arr[ $j] = $tmp; } else { //如果碰到不需要移动的元素 //由于是已经排序好是数组，则前面的就不需要再次比较了。 break; } } } //将这个元素 插入到已经排序好的序列内。 //返回 return $arr; } 六、希尔排序 介绍： 希尔排序，也称递减增量排序算法，是插入排序的一种高速而稳定的改进版本。 希尔排序是基于插入排序的以下两点性质而提出改进方法的： 1、插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率 2、但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位> 排序效果： <br/> 七、归并排序 介绍： 归并排序（Merge sort，台湾译作：合并排序）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（pide and Conquer）的一个非常典型的应用 步骤： 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列 设定两个指针，最初位置分别为两个已经排序序列的起始位置 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置 重复步骤3直到某一指针达到序列尾 将另一序列剩下的所有元素直接复制到合并序列尾 排序效果： 我们先来看看主函数部分： 在总函数中，我们只调用了一个 MSort() 函数，因为我们要使用递归调用，所以将 MSort() 封装起来。 下面我们来看看 MSort() 函数： 上面的 MSort() 函数实现将数组分半再分半（直到子序列长度为1），然后将子序列合并起来。 现在是我们的归并操作函数 Merge() : 到了这里，我们的归并算法就完了。我们调用试试： 相关推荐： Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
<br/><br/>
Copier après la connexion
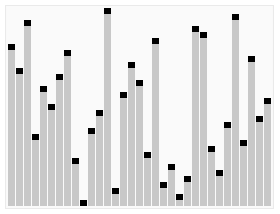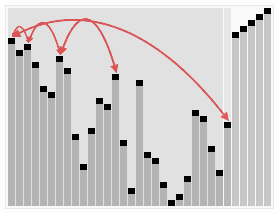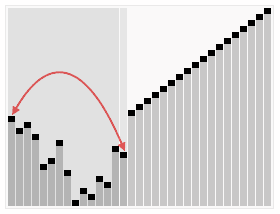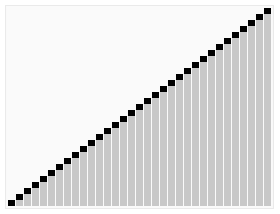<br/>function heapSort($arr) {
$len = count($arr); // 先建立最大堆
for ($i = floor(($len - 1) / 2); $i >= 0; $i--) { $s = $i; $childIndex = $s * 2 + 1; while ($childIndex < $len) { // 在父、左子、右子中 ，找到最大的
if ($childIndex + 1 < $len && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} // 从最后一个元素开始调整
for ($i = $len - 1; $i > 0; $i--) { $t = $arr[$i]; $arr[$i] = $arr[0]; $arr[0] = $t; // 调整第一个元素
$s = 0; $childIndex = 1; while ($childIndex < $i) { // 在父、左子、右子中 ，找到最大的
if ($childIndex + 1 < $i && $arr[$childIndex] < $arr[$childIndex + 1]) $childIndex++; if ($arr[$s] < $arr[$childIndex]) { $t = $arr[$s]; $arr[$s] = $arr[$childIndex]; $arr[$childIndex] = $t; $s = $childIndex; $childIndex = $childIndex * 2 + 1;
} else { break;
}
}
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr));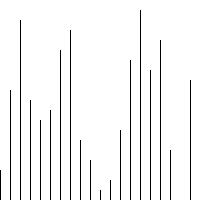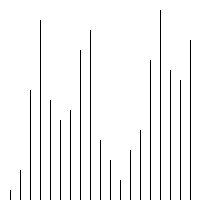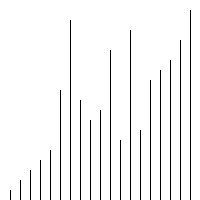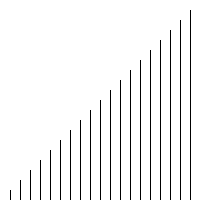Copier après la connexion
<br/>感觉插入排序跟冒泡排序有点相似，时间复杂度也是O(n^2)，实现代码如下：<br/>
Copier après la connexion
<br/>希尔排序其实可以理解是插入排序的一个优化版，它的效率跟增量有关，增量要取多少，根据不同的数组是不同的，所以希尔排序是一个不稳定的排序算法，它的时间复杂度为O(nlogn)到O(n^2)之间，实现代码如下：function shellSort($arr) {
$len = count($arr); $stepSize = floor($len / 2); while ($stepSize >= 1) { for ($i = $stepSize; $i < $len; $i++) { if ($arr[$i] < $arr[$i - $stepSize]) { $t = $arr[$i]; $j = $i - $stepSize; while ($j >= 0 && $t < $arr[$j]) { $arr[$j + $stepSize] = $arr[$j]; $j -= $stepSize;
} $arr[$j + $stepSize] = $t;
}
} // 缩小步长，再进行插入排序
$stepSize = floor($stepSize / 2);
} return $arr;
}$arr = [3,1,13,5,7,11,2,4,14,9,15,6,12,10,8];
print_r(bubbleSort($arr));Copier après la connexion
<br/>归并排序的时间复杂度也是O(nlogn)。原理是：对于两个排序好的数组，分别遍历这两个数组，获取较小的元素插入新的数组中，那么，这么新的数组也会是排序好的。代码如下：//交换函数function swap(array &$arr,$a,$b){
$temp = $arr[$a]; $arr[$a] = $arr[$b]; $arr[$b] = $temp;
}//归并算法总函数function MergeSort(array &$arr){
$start = 0; $end = count($arr) - 1;
MSort($arr,$start,$end);
}Copier après la connexionfunction MSort(array &$arr,$start,$end){ //当子序列长度为1时，$start == $end，不用再分组 if($start < $end){ $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end] MSort($arr,$start,$mid); //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid] MSort($arr,$mid + 1,$end); //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end] Merge($arr,$start,$mid,$end); //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
}
}Copier après la connexion//归并操作function Merge(array &$arr,$start,$mid,$end){
$i = $start; $j=$mid + 1; $k = $start; $temparr = array(); while($i!=$mid+1 && $j!=$end+1)
{ if($arr[$i] >= $arr[$j]){ $temparr[$k++] = $arr[$j++];
} else{ $temparr[$k++] = $arr[$i++];
}
} //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($i != $mid+1){ $temparr[$k++] = $arr[$i++];
} //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
while($j != $end+1){ $temparr[$k++] = $arr[$j++];
} for($i=$start; $i<=$end; $i++){ $arr[$i] = $temparr[$i];
}
}Copier après la connexion$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);
Copier après la connexion
Algorithme de remplacement de page
Comment ouvrir le fichier php
Quelles sont les méthodes de tri ?
Comment supprimer les premiers éléments d'un tableau en php
Que faire si la désérialisation php échoue
Comment connecter PHP à la base de données mssql
Comment connecter PHP à la base de données mssql
Comment télécharger du HTML
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
