Comment implémenter un arbre de recherche binaire en Python

Arbre

Binaire Recherche (arbre de tri binaire). La structure de données de chaque nœud est composée de 1 pointeur de nœud parent, 1 pointeur enfant gauche, 1 pointeur enfant et lui-même. le nœud.

Arbre de recherche binaire

Nous connaissons déjà deux façons différentes d'obtenir des paires clé-valeur dans une collection. Rappelez-vous comment ces collections implémentent ADT (AbstractData Type)MAP. Nous discutons de deux implémentations d'ADT MAP, de la recherche binaire basée sur des listes et de la table de hachage. Dans cette section, nous allons découvrir les arbres de recherche binaires, qui sont une autre collection Map dont les clés pointent vers des valeurs. Dans ce cas, nous n'avons pas besoin de considérer la position réelle de l'élément dans l'arbre, mais nous devons la connaître. comment utiliser les arbres binaires pour rechercher plus d'informations. Soyez efficace.

Opérations sur l'arbre de recherche

Avant d'examiner cette implémentation, passons en revue l'interface fournie par ADT MAP. On remarquera que cette interface est très similaire au dictionnaire Python.

1. Map() crée une nouvelle collection Map vide.

2. put(key,val) ajoute une nouvelle paire clé-valeur à la carte. Si la clé est déjà dans la Map, la nouvelle valeur est utilisée pour remplacer l'ancienne valeur.

3. get(key) Fournit une clé, renvoie les données enregistrées dans la carte ou renvoie Aucune.

4. del Utilisez l'instruction del map[key] pour supprimer la paire clé-valeur de la carte.

5. len() renvoie le nombre de paires clé-valeur enregistrées dans la carte

6. in Si la clé donnée est dans la carte, utilisez entrez L'instruction map renvoie True.

Implémentation de l'arbre de recherche

Un arbre de recherche binaire, si les valeurs clés du sous-arbre de gauche sont inférieures à celles du parent node, Les valeurs clés dans le sous-arbre droit sont supérieures à l'attribut du nœud parent. Nous appelons cet arbre un arbre de recherche BST. Comme mentionné précédemment, lorsque nous implémenterons Map, la méthode BST nous guidera pour y parvenir. La figure 1 illustre cette propriété d'un arbre de recherche binaire, montrant les clés qui n'ont aucune valeur associée. Notez que cette propriété s'applique à chaque nœud parent et nœud enfant. Toutes les clés du sous-arbre gauche sont inférieures à la clé du nœud racine et toutes les clés du sous-arbre droit sont supérieures à la clé du nœud racine.

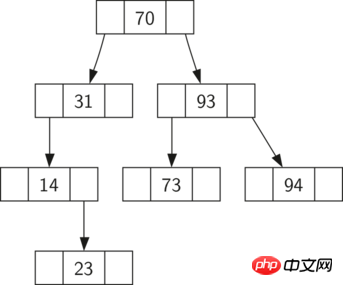
Figure 1 : Un arbre de recherche binaire simple

Maintenant que vous savez ce qu'est un arbre de recherche binaire, voyons comment construire un arbre de recherche binaire Arbre de recherche, nous insérons ces valeurs clés dans l'arbre de recherche dans l'ordre des nœuds indiqués sur la figure 1. Les nœuds dans l'arbre de recherche de la figure 1 sont : 70, 31, 93, 94, 14, 23, 73. Étant donné que 70 est la première valeur insérée dans l’arborescence, il s’agit du nœud racine. Ensuite, 31 est inférieur à 70 et donc le sous-arbre gauche de 70. Ensuite, 93 est supérieur à 70 et donc le sous-arbre droit de 70. Nous avons maintenant rempli deux niveaux de l'arborescence, donc la valeur clé suivante sera soit le sous-arbre gauche ou droit de 31 ou 93. Puisque 94 est supérieur à 70 et 93, il devient le sous-arbre droit de 93. De même, 14 est plus petit que 70 et 31, il devient donc le sous-arbre gauche de 31. 23 est également inférieur à 31, il doit donc s'agir du sous-arbre gauche de 31. Cependant, il est supérieur à 14, c’est donc le bon sous-arbre de 14.

Pour implémenter un arbre de recherche binaire, nous utiliserons des nœuds et des références à , de la même manière que nous implémentons des listes chaînées et des expressions arbres. Parce que nous devons être capables de créer et d'utiliser un arbre de recherche binaire vide, nous le ferons en utilisant deux classes, la première classe que nous appellerons BinarySearchTree et la deuxième classe que nous appellerons TreeNode. La classe BinarySearchTree a une référence à la classe TreeNode comme racine de l'arbre de recherche binaire. Dans la plupart des cas, la classe externe définit la méthode externe de qui vérifie simplement si l'arborescence est vide et s'il y a un. nœud dans l'arborescence, l'exigence La classe BinarySearchTree contient des méthodes privées qui définissent la racine en tant que paramètre. Dans ce cas, si l’arborescence est vide ou si l’on souhaite supprimer la racine de l’arborescence, nous devons utiliser des opérations spéciales. Le code du constructeur et quelques autres fonctions de la classe BinarySearchTree sont présentés dans le listing 1.

Liste 1

class BinarySearchTree:

  def init(self):
    self.root = None
    self.size = 0

  def length(self):
    return self.size

  def len(self):
    return self.size

  def iter(self):
    return self.root.iter()

La classe TreeNode fournit de nombreuses fonctions auxiliaires pour faciliter le processus d'implémentation des méthodes de la classe BinarySearchTree. Comme le montre le listing 2, la structure d'un nœud d'arbre est implémentée par ces fonctions auxiliaires. Comme vous pouvez le voir, ces fonctions d'assistance peuvent diviser un nœud en enfant gauche ou droit en fonction de sa position et du type de cet enfant. La classe TreeNode suit très clairement les propriétés de chaque nœud parent. Vous verrez pourquoi c'est important lorsque nous discuterons de l'implémentation de l'opération de suppression.

Une autre chose intéressante à propos de l'implémentation de TreeNode dans le listing 2 est que nous utilisons les paramètres facultatifs de Python. Les paramètres facultatifs facilitent la création d'un nœud d'arborescence dans plusieurs situations différentes. Parfois, nous souhaitons créer un nouveau nœud d'arborescence même si nous avons déjà un nœud parent et un nœud enfant. Comme les nœuds parent et enfant existants, nous pouvons transmettre les nœuds parent et enfant en tant que paramètres. Parfois, nous créons également un arbre contenant des paires clé-valeur et nous ne transmettons aucun paramètre pour les nœuds parents ou enfants. Dans ce cas nous utiliserons les valeurs par défaut des paramètres facultatifs.

Listing 2

class TreeNode:
  def init(self,key,val,left=None,right=None,
                    parent=None):
    self.key = key
    self.payload = val
    self.leftChild = left
    self.rightChild = right
    self.parent = parent

  def hasLeftChild(self):
    return self.leftChild

  def hasRightChild(self):
    return self.rightChild

  def isLeftChild(self):
    return self.parent and self.parent.leftChild == self

  def isRightChild(self):
    return self.parent and self.parent.rightChild == self

  def isRoot(self):
    return not self.parent

  def isLeaf(self):
    return not (self.rightChild or self.leftChild)

  def hasAnyChildren(self):
    return self.rightChild or self.leftChild

  def hasBothChildren(self):
    return self.rightChild and self.leftChild

  def replaceNodeData(self,key,value,lc,rc):
    self.key = key
    self.payload = value
    self.leftChild = lc
    self.rightChild = rc
    if self.hasLeftChild():
      self.leftChild.parent = self
    if self.hasRightChild():
      self.rightChild.parent = self

Maintenant que nous avons les classes BinarySearchTree et TreeNode, il est temps d'écrire une méthode put qui nous permet de construire un binaire arbre de recherche. La méthode put est une méthode de la classe BinarySearchTree. Cette méthode vérifiera si l'arbre est déjà enraciné. Sinon, nous créerons un nouveau nœud d’arbre et le définirons comme racine de l’arbre. S'il existe déjà un nœud racine, nous l'appelons lui-même, effectuons une récursion, et utilisons la fonction auxiliaire _put pour rechercher dans l'arbre selon l'algorithme suivant :

Partir du nœud racine de l'arbre et recherchez l'arbre binaire par Pour comparer la nouvelle valeur de clé avec la valeur de clé du nœud actuel, si la nouvelle valeur de clé est inférieure à celle du nœud actuel, recherchez dans le sous-arbre de gauche. Si la nouvelle clé est supérieure au nœud actuel, le sous-arbre de droite est recherché.

Lorsque le sous-arbre gauche (ou droit) ne peut pas être recherché, notre position dans l'arborescence est celle où le nouveau nœud est défini.
Pour ajouter un nœud à l'arborescence, créez un nouvel objet TreeNode et insérez cet objet dans le nœud précédant immédiatement ce point.

Le listing 3 montre le code Python pour insérer un nouveau nœud dans l'arborescence. La fonction _put doit suivre les étapes ci-dessus pour écrire un algorithme récursif. Notez que lorsqu'un nouveau sous-arbre est inséré, le nœud actuel (CurrentNode) est transmis au nouvel arbre en tant que nœud parent.

Un problème important lorsque nous effectuons l'insertion est que les valeurs de clé en double ne peuvent pas être traitées correctement. Notre arbre implémente la réplication des valeurs de clé, ce qui créera un nouveau nœud dans le sous-arbre de droite avec la même valeur de clé que l'original. nœud nœud. La conséquence est que de nouveaux nœuds ne seront pas découverts lors de la recherche. Nous utilisons une meilleure façon de gérer l'insertion de valeurs de clé en double, où l'ancienne valeur est remplacée par la valeur associée à la nouvelle clé. Nous vous laissons le correctif de ce bug sous forme de exercice.

Listing 3

def put(self,key,val):
  if self.root:
    self._put(key,val,self.root)
  else:
    self.root = TreeNode(key,val)
  self.size = self.size + 1

def _put(self,key,val,currentNode):
  if key < currentNode.key:
    if currentNode.hasLeftChild():
        self._put(key,val,currentNode.leftChild)
    else:
        currentNode.leftChild = TreeNode(key,val,parent=currentNode)
  else:
    if currentNode.hasRightChild():
        self._put(key,val,currentNode.rightChild)
    else:
        currentNode.rightChild = TreeNode(key,val,parent=currentNode)

Avec l'implémentation de la méthode put, on peut facilement passer la méthode setitem surchargez [] en tant qu'opérateur pour appeler la méthode put (voir Listing 4). Cela nous permet d'écrire des instructions python comme myZipTree['Plymouth'] = 55446, qui ressemble à un dictionnaire Python.

Listing 4

def setitem(self,k,v):
  self.put(k,v)

La figure 2 illustre le processus d'insertion d'un nouveau nœud dans un arbre de recherche binaire. Les nœuds gris montrent l'ordre des nœuds de l'arborescence traversés pendant le processus d'insertion.

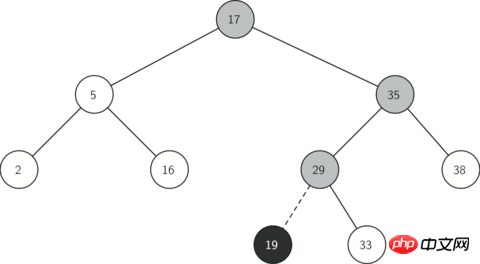
Figure 2 : Insertion d'un nœud avec une valeur clé = 19

Une fois l'arbre construit, la tâche suivante consiste à l'implémenter pour une valeur clé donnée Récupérer. La méthode get est plus simple que la méthode put car elle recherche simplement l'arborescence de manière récursive jusqu'à ce qu'un nœud feuille incompatible soit trouvé ou qu'une valeur de clé correspondante soit trouvée. Lorsqu'une valeur de clé correspondante est trouvée, la valeur dans le nœud est renvoyée.

Le listing 5 montre le code pour get, _get et getitem. Le code recherché avec la méthode _get a la même logique de sélection du sous-arbre gauche ou droit que la méthode put. Veuillez noter que la méthode _get renvoie la valeur de get dans TreeNode. _get peut être utilisée comme un moyen flexible et efficace de fournir des paramètres pour d'autres méthodes de BinarySearchTree qui peuvent avoir besoin d'utiliser des données dans TreeNode.

En implémentant la méthode getitem, nous pouvons écrire une instruction Python qui donne l'impression que nous accédons à un dictionnaire, alors qu'en fait nous exploitons simplement un arbre de recherche binaire, tel que Z = myziptree['fargo']. Comme vous pouvez le voir, la méthode getitem appelle get.

Liste 5

def get(self,key):
  if self.root:
    res = self._get(key,self.root)
    if res:
        return res.payload
    else:
        return None
  else:
    return None

def _get(self,key,currentNode):
  if not currentNode:
    return None
  elif currentNode.key == key:
    return currentNode
  elif key < currentNode.key:
    return self._get(key,currentNode.leftChild)
  else:
    return self._get(key,currentNode.rightChild)

def getitem(self,key):
  return self.get(key)

使用get，我们可以通过写一个BinarySearchTree的contains方法来实现操作，contains方法简单地调用了get方法，如果它有返回值就返回True，如果它是None就返回False。如Listing 6 所示。

Listing 6

def contains(self,key):
  if self._get(key,self.root):
    return True
  else:
    return False

回顾一下contains重载的操作符，这允许我们写这样的语句：

if 'Northfield' in myZipTree:
  print("oom ya ya")

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!