
1514. Chemin avec probabilité maximale
Difficulté :Moyen
Sujets : Tableau, graphique, tas (file d'attente prioritaire), chemin le plus court
Vous recevez un graphe pondéré non orienté de n nœuds (indexés 0), représenté par une liste d'arêtes où edge[i] = [a, b] est une arête non orientée reliant les nœuds a et b avec une probabilité de succès de traverser ce bord succProb[i].
Étant donné le début et la fin de deux nœuds, trouver le chemin avec la probabilité maximale de succès pour aller du début à la fin et renvoyer sa probabilité de succès.
S'il n'y a pas de chemin du début à la fin, renvoie 0. Votre réponse sera acceptée si elle diffère de la bonne réponse d'au plus 1e-5.
Exemple 1 :
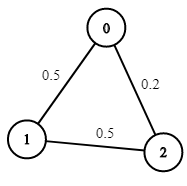
Exemple 2 :
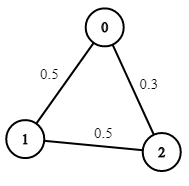
Exemple 3 :
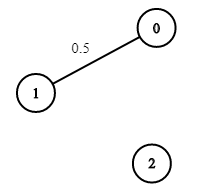
Contraintes :
Indice :
Solution :
Nous pouvons utiliser une version modifiée de l'algorithme de Dijkstra. Au lieu de trouver le chemin le plus court, vous maximiserez les chances de succès.
Implémentons cette solution en PHP : 1514. Chemin avec probabilité maximale
<?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @param Float[] $succProb
* @param Integer $start_node
* @param Integer $end_node
* @return Float
*/
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;
echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000
$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;
echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000
$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;
echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>
<h3>
Explication:
</h3>
<ol>
<li><p><strong>Représentation graphique</strong> : Le graphique est représenté comme une liste de contiguïté où chaque nœud pointe vers ses voisins ainsi que les probabilités de succès des arêtes qui les relient.</p></li>
<li><p><strong>Tableau de probabilité maximale</strong> : Un tableau maxProb est utilisé pour stocker la probabilité maximale d'atteindre chaque nœud à partir du nœud de départ.</p></li>
<li><p><strong>File d'attente prioritaire</strong> : Un tas maximum (SplPriorityQueue) est utilisé pour explorer en premier les chemins avec la probabilité la plus élevée. Ceci est crucial pour garantir que lorsque nous atteignons le nœud de destination, nous avons trouvé le chemin avec la probabilité maximale.</p></li>
<li>
<p><strong>Algorithme</strong> :</p>
<ul>
<li>Initialisez la probabilité du nœud de départ à 1 (puisque la probabilité de rester au départ est de 1).</li>
<li>Utilisez la file d'attente prioritaire pour explorer les nœuds, en mettant à jour la probabilité maximale d'atteindre chaque voisin.</li>
<li>Si le nœud de destination est atteint, renvoie la probabilité.</li>
<li>Si aucun chemin n'existe, renvoie 0.</li>
</ul>
</li>
</ol>
<h3>
Sortir:
</h3>
<p>Pour l'exemple fourni :<br>
</p>
<pre class="brush:php;toolbar:false">$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;
La sortie sera de 0,25.
Cette approche garantit une solution efficace utilisant l'algorithme de Dijkstra tout en gérant les spécificités des calculs de probabilité.
Liens de contact
Si vous avez trouvé cette série utile, pensez à donner une étoile au référentiel sur GitHub ou à partager la publication sur vos réseaux sociaux préférés ?. Votre soutien signifierait beaucoup pour moi !
Si vous souhaitez du contenu plus utile comme celui-ci, n'hésitez pas à me suivre :
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 A quoi sert Java
A quoi sert Java
 Que dois-je faire si mon compte QQ est volé ?
Que dois-je faire si mon compte QQ est volé ?
 Comment ouvrir des fichiers HTML
Comment ouvrir des fichiers HTML
 Comment désactiver les mises à jour automatiques dans Win10
Comment désactiver les mises à jour automatiques dans Win10
 Solution aux caractères tronqués lors de l'ouverture d'Excel
Solution aux caractères tronqués lors de l'ouverture d'Excel
 Modifier le nom du fichier sous Linux
Modifier le nom du fichier sous Linux
 Comment utiliser des vidéos en Java
Comment utiliser des vidéos en Java
 Quelles sont les pièces inscrites ?
Quelles sont les pièces inscrites ?