Nombre maximum de points avec coût

1937. Nombre maximum de points avec coût

Difficulté :Moyen

Sujets :Array, Programmation dynamique

Vous recevez une matrice entière m x n points (0-indexés). En commençant avec 0 point, vous souhaitezmaximiserle nombre de points que vous pouvez obtenir de la matrice.

Pour gagner des points, vous devez choisir une cellule danschaque ligne. Choisir la cellule aux coordonnées (r, c)ajouterapoints[r][c] à votre score.

Cependant, vous perdrez des points si vous choisissez une cellule trop éloignée de la cellule que vous avez sélectionnée dans la ligne précédente. Pour deux lignes adjacentes r et r + 1 (où 0 <= r < m - 1), la sélection de cellules aux coordonnées (r, c₁) et (r + 1, c₂)soustrairaabdos (c₁- c₂) de votre score.

Rendezlenombre maximumde points que vous pouvez obtenir.

abs(x) est défini comme :

• x pour x >= 0.

• -x pour x < 0.

Exemple 1 :

• Entrée :l1 = [2,4,3], l2 = [5,6,4]
• Sortie :9
• Explication :
  • Les cellules bleues désignent les cellules optimales à sélectionner, qui ont les coordonnées (0, 2), (1, 1) et (2, 0).
  • Vous ajoutez 3 + 5 + 3 = 11 à votre score.
  • Cependant, vous devez soustraire abs(2 - 1) + abs(1 - 0) = 2 de votre score.
  • Votre score final est de 11 - 2 = 9.

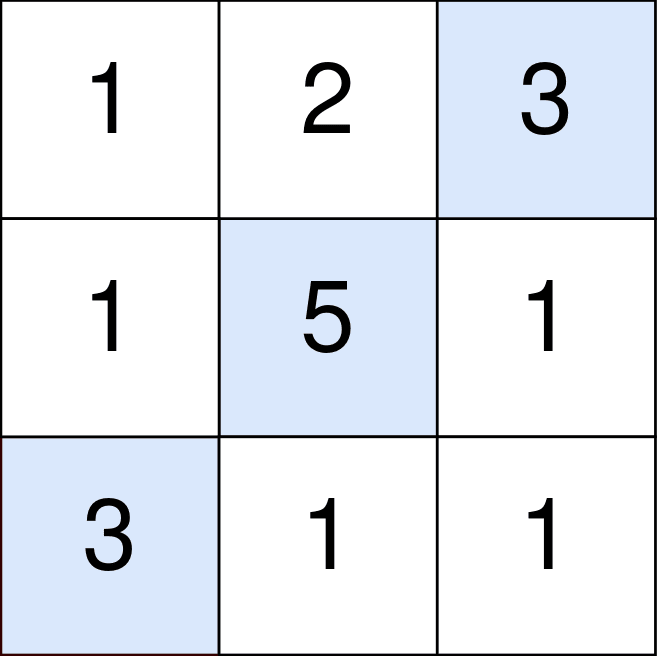
Exemple 2 :

• Entrée :points = [[1,5],[2,3],[4,2]]
• Sortie :11
• Explication :
  • Les cellules bleues désignent les cellules optimales à sélectionner, qui ont les coordonnées (0, 1), (1, 1) et (2, 0).
  • Vous ajoutez 5 + 3 + 4 = 12 à votre score.
  • Cependant, vous devez soustraire abs(1 - 1) + abs(1 - 0) = 1 de votre score.
  • Votre score final est de 12 - 1 = 11.

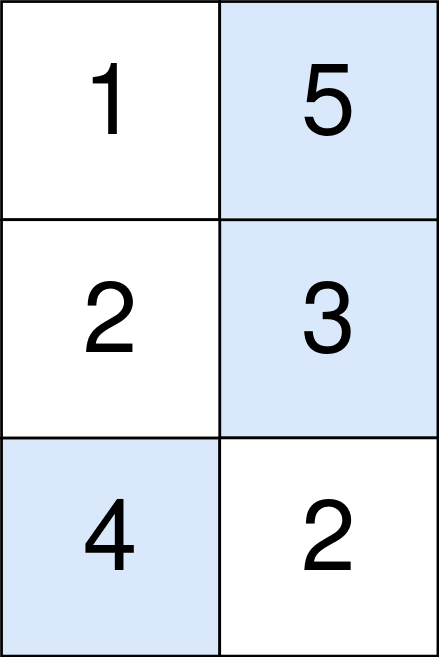
Contraintes :

• m == points.longueur
• n == points[r].longueur
• 1 <= m, n <= 10⁵
• 1 <= m * n <= 10⁵
• 0 <= points[r][c] <= 10⁵

Indice :

1. Essayez d'utiliser la programmation dynamique.
2. dp[i][j] est le nombre maximum de points que vous pouvez avoir si points[i][j] est la cellule la plus récente que vous avez sélectionnée.

Solution :

Nous pouvons décomposer la solution en plusieurs étapes :

Étape 1 : Définir le tableau DP

Nous utiliserons un tableau 2D dp où dp[i][j] représente le maximum de points que nous pouvons obtenir en sélectionnant la cellule de la ligne i et de la colonne j.

Étape 2 : initialiser la matrice DP

Initialisez la première ligne de dp pour qu'elle soit identique à la première ligne de points car il n'y a pas de lignes précédentes pour soustraire le coût.

Étape 3 : Calculer les valeurs DP pour chaque ligne

Pour chaque ligne suivante, nous calculons le maximum de points possibles pour chaque colonne en tenant compte des coûts de passage de la ligne précédente.

Pour calculer efficacement la transition de la ligne i-1 à la ligne i, nous pouvons utiliser deux tableaux auxiliaires gauche et droite :

• left[j] stockera la valeur maximale que nous pouvons atteindre pour la j-ième colonne en considérant uniquement les transitions depuis la gauche.
• right[j] stockera la valeur maximale que nous pouvons atteindre pour la j-ième colonne en considérant uniquement les transitions depuis la droite.

Étape 4 : mettre à jour DP pour chaque ligne

Pour chaque colonne j de la ligne i :

• Mettez à jour dp[i][j] en utilisant le maximum de gauche[j] ou de droite[j] plus les points[i][j].

Étape 5 : renvoyer la valeur maximale de la dernière ligne

Le résultat sera la valeur maximale dans la dernière ligne du tableau dp.

Implémentons cette solution en PHP :1937. Nombre maximum de points avec coût

        
Explication:
        

         
Tableaux gauche et droit :Ceux-ci nous aident à calculer le maximum de points que nous pouvons gagner pour chaque cellule en considérant les valeurs de la ligne précédente, en tenant compte efficacement de la pénalité liée au déplacement entre les colonnes.
         
Approche de programmation dynamique :Cette méthode garantit que chaque ligne est calculée en fonction de la ligne précédente, ce qui rend la solution évolutive pour les grandes matrices.
        
Cette approche a une complexité temporelle de (O(m fois n)), ce qui est efficace compte tenu des contraintes.
Liens de contact
이 시리즈가 도움이 되었다면repository에 별점을 주거나 좋아하는 소셜 네트워크에 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!
이런 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요:
        

         
LinkedIn
         
GitHub
        
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!