Dans le monde trépidant de la finance, la précision est primordiale. C'est toujours mieux d'éviter une perte d'un million de dollars à cause d'une erreur d'arrondi/précision.
Le point de départ de cet article est la prise de conscience que l’argent n’est pas votre nombre de base moyen que vous pouvez utiliser pour compter les pommes dans votre panier. Qu'obtient-on lorsque l'on essaie de multiplier 10€ par 10$ ? Difficile, hein… Avez-vous déjà trouvé un montant miraculeux de 1,546 $ dans la poche d'une vieille veste ? Ouais, je sais, ce n'est pas vraiment possible non plus. Ces exemples idiots sont là pour illustrer le fait que l’argent a ses propres règles particulières et ne peut pas être modélisé uniquement par un simple nombre. Je vous rassure, je ne suis pas le premier à m'en rendre compte (et peut-être que vous l'avez réalisé bien avant moi). En 2002, le programmeur Martin Fowler a proposé dans les Patterns of Enterprise Application Architecture une manière de représenter l'argent, avec des attributs et des règles d'opérandes spécifiques. Pour lui, les deux attributs minimaux viables nécessaires pour un type de données money étaient :
amount currency
Cette représentation vraiment basique sera notre point de départ pour construire un modèle monétaire simple mais robuste.
Un montant en argent est bien un nombre particulier : il a une précision fixe (encore une fois, vous ne pouvez pas avoir 4,376$ en poche). Vous devez choisir une manière de le représenter qui vous aide à respecter cette contrainte.
Alerte spoiler, ce n'est certainement pas une bonne idée si vous ne voulez pas voir quelques centimes (si ce n'est pas des dollars) disparaître dans le monde sombre de la représentation des nombres à virgule flottante.
Si vous avez une certaine expérience du codage en JavaScript, vous savez que même le calcul le plus simple peut entraîner une erreur de précision à laquelle vous ne vous attendriez pas au début. L'exemple le plus évident et le plus connu pour mettre en évidence ce phénomène est :
0.1 + 0.2 !== 0.3 // true 0.1 + 0.2 // 0.30000000000000004
Si cet exemple ne vous convainc pas entièrement, je vous conseille de jeter un œil à cet article qui approfondit un peu plus tous les résultats de calcul problématiques que vous pouvez rencontrer en travaillant avec le type de nombre natif JavaScript…
Ce léger delta dans les résultats peut vous paraître inoffensif (avec une ampleur d'environ ~ 10^-16), cependant dans une application financière critique, une telle erreur peut se produire rapidement. Envisagez de transférer des fonds entre des milliers de comptes, où chaque transaction implique des calculs similaires. Les légères inexactitudes s’additionnent et avant que vous vous en rendiez compte, vos états financiers sont erronés de plusieurs milliers de dollars. Et honnêtement, nous pouvons tous convenir qu'en matière d'argent, l'erreur n'est pas permise : tant sur le plan juridique que pour construire une relation de confiance avec vos clients.
La première question que je me suis posée lorsque j'ai rencontré le problème dans l'un de mes projets est pourquoi ? J'ai découvert que la source du problème n'est pas JavaScript et que ces imprécisions affectent également d'autres langages de programmation modernes (Java, C, Python, …).
// In C
#include <stdio.h>
int main() {
double a = 0.1;
double b = 0.2;
double sum = a + b;
if (sum == 0.3) {
printf("Equal\n");
} else {
printf("Not Equal\n"); // This block is executed
}
return 0;
}
// > Not equal
// In Java
public class doublePrecision {
public static void main(String[] args) {
double total = 0;
total += 5.6;
total += 5.8;
System.out.println(total);
}
}
// > 11.399999999999
En fait, la cause profonde réside dans la norme utilisée par ces langages pour représenter les nombres à virgule flottante : le format à virgule flottante double (ou simple) précision, spécifié par la norme IEEE 754.
En Javascript, le nombre de type natif correspond à des nombres à virgule flottante double précision, ce qui signifie qu'un nombre est codé sur 64 bits et divisé en trois parties :
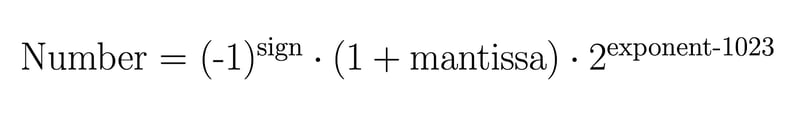
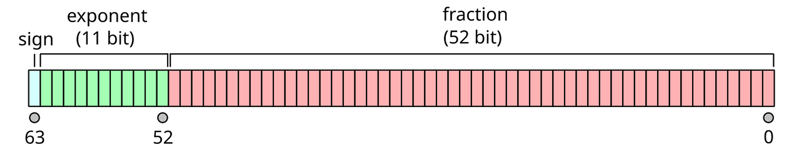
Ensuite, vous devez utiliser la formule suivante pour convertir votre représentation binaire en valeur décimale :
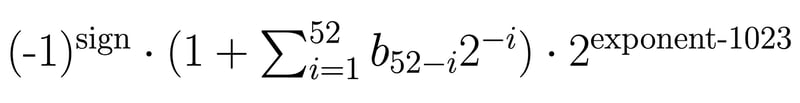
Un exemple de représentation de nombres à virgule flottante double précision, une approximation de 1/3 :
0 01111111101 0101010101010101010101010101010101010101010101010101 = (-1)^0 x (1 + 2^-2 + 2^-4 + 2^-6 + ... + 2^-50 + 2^-52) x 2^(1021-1023) = 0.333333333333333314829616256247390992939472198486328125 ~ 1/3
This format allows us to represent a vast range of values, but it can't represent every possible number with absolute precision (just between 0 and 1 you can find an infinity of numbers…). Many numbers cannot be represented exactly in binary form. To loop on the first example, that's the issue with 0.1 and 0.2. Double-point floating representation gives us an approximation of these value, so when you add these two imprecise representations, the result is also not exact.
Now that you are fully convinced that handling money amounts with native JavaScript number type is a bad idea (at least I hope you begin to have doubts about it), the 1Billion$ question is how should you proceed ? A solution could be to make use of some of the powerful fixed-precision arithmetic packages available in JavaScript. For example Decimal.js (which is used by the popular ORM Prisma to represent its Decimal datatype) or Big.js.
These packages provide you with special datatypes that allow you to perform calculations with getting rid of precision errors we explained above.
// Example using Decimal.js
const Decimal = require('decimal.js');
const a = new Decimal('0.1');
const b = new Decimal('0.2');
const result = a.plus(b);
console.log(result.toString()); // Output: '0.3'
This approach provides you with another advantage, it drastically extends the maximum value that can be represented, which can become pretty handy when you are dealing with cryptocurrencies for example.
Even if it is really robust, that it not the one I prefer to choose to implement in my web applications. I find it easier and clearer to apply Stripe strategy to only deal with integer values.
We, at Theodo Fintech, value pragmatism! We love to take inspiration from the most succeeding companies in the industry. Stripe, the well-known billions$ company specialized in payment services, made the choice to handle money amounts without floating numbers but with integers. To do that, they use the smallest unit of the currency to represent a monetary amount.
// 10 USD are represented by
{
"amount": 1000,
"currency": "USD"
}
I guess that many of you already know this: all currencies don't have the smallest unit of the same magnitude. Most of them are "two-decimal" currencies (EUR, USD, GBP) which means that their smallest unit is 1/100th of the currency. However, some are "three-decimal" currencies (KWD) or even "zero-decimal" currencies (JPY). (You can find more information about it by following the ISO4217 standard). To handle these disparities, you should integrate to your money data representation the multiplicative factor to convert an amount represented in the smallest unit into the corresponding currency.
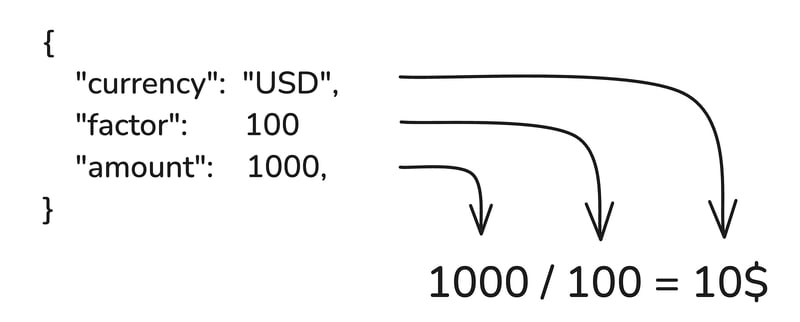
I guess you already figured it out, you can either work with native number , third party arbitrary-precision packages or integers, calculations can (and will) lead you to floating-point results that you will need to round to your monetary finite precision. As a quick example is never to much, let's say that you handle integer values and contracted a loan of 16k$ with a really precise interest rate of 8.5413% (ouch…). You then need to refund 16k$ plus an additional amount of
1600000 * 0.085413 // amount in cents //Output in cents: 136660.8
The crux is to properly handle the rounding process of money amounts after calculations. Most of the time, you end up having to choose between three different kinds of rounding:
When it comes to roundings, there is not really any "magic sauce": you need to arbitrate depending on your situation. I recommend you always check legislation when you deal with a new currency and a new rounding use case (conversion, money split, interest rates for credits, …). You better follow regulations right away to avoid further troubles. For example, when it comes to conversion rates, most currencies have determined rules about needed precision and rounding rules (you can have a look at the EUR conversion rate rules here).
Cet article n'est pas exhaustif sur toutes les possibilités existantes pour gérer des sommes d'argent en JavaScript et n'est pas non plus destiné à vous fournir un modèle de données monétaires complet/parfait. J'ai essayé de vous donner suffisamment d'indices et de lignes directrices pour mettre en place une représentation qui s'est avérée cohérente, résiliente et qui a été choisie par les grands acteurs de l'industrie fintech. J'espère que vous pourrez effectuer des calculs de montants d'argent dans vos futurs projets sans oublier un seul centime en poche (sinon n'oubliez pas de jeter un oeil dans votre ancienne veste) !
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
numéro python en chaîne
Le rôle de Vulkan
Que faire si phpmyadmin ne parvient pas à importer le fichier SQL
Introduction au document en JS
La différence entre la carte MS et la carte SD
Comment faire correspondre les nombres dans les expressions régulières
Que signifie le clonage WeChat ?
Les principaux composants du dhtml
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
