Un voyage à travers les algorithmes en utilisant Javascript - Bubble Sort

Qu’est-ce que le tri à bulles ?

Bubble Sort est l’un des algorithmes de tri les plus simples en informatique. Nommé pour la façon dont les éléments plus petits « bullent » en haut de la liste à chaque itération, c'est un excellent outil pour enseigner les bases des algorithmes de tri. Bien qu'il ne soit pas le plus efficace pour les grands ensembles de données, sa simplicité en fait un excellent point de départ pour comprendre le fonctionnement des algorithmes de tri.

Comment fonctionne le tri à bulles

Bubble Sort fonctionne en parcourant la liste à plusieurs reprises, en comparant les éléments adjacents et en les échangeant s'ils sont dans le mauvais ordre. Ce processus est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, indiquant que la liste est triée.

Voici une répartition étape par étape :

1. Commencez par le premier élément du tableau.
2. Comparez-le avec l'élément suivant.
3. Si le premier élément est supérieur au second, échangez-les.
4. Passez à l'élément suivant et répétez les étapes 2 à 3 jusqu'à ce que vous atteigniez la fin du tableau.
5. Si des échanges ont été effectués, répétez le processus depuis le début.
6. Si aucun échange n'a été effectué lors d'une passe complète, le tableau est trié.

Visualisons ce processus :

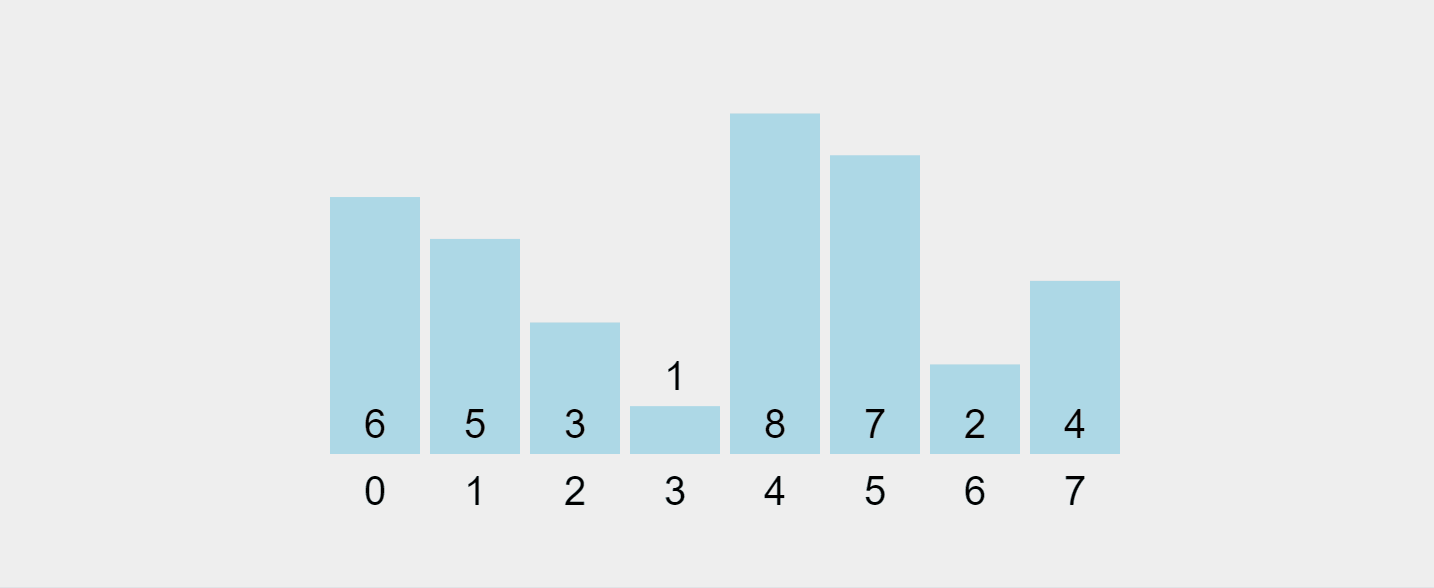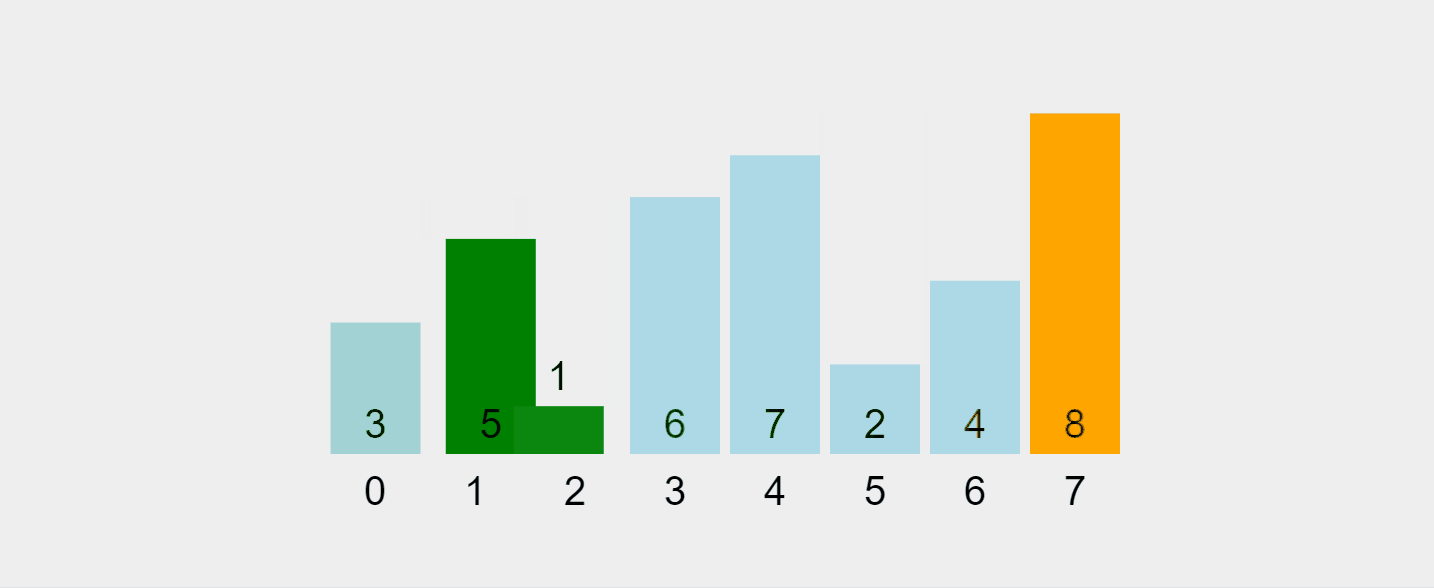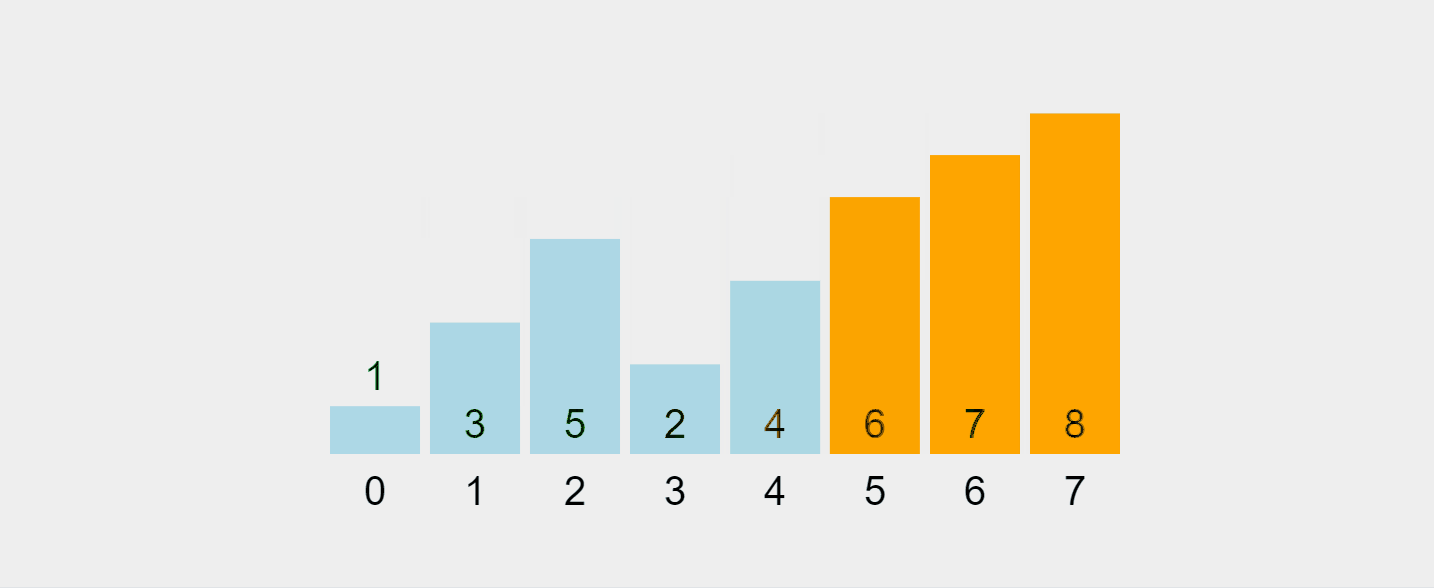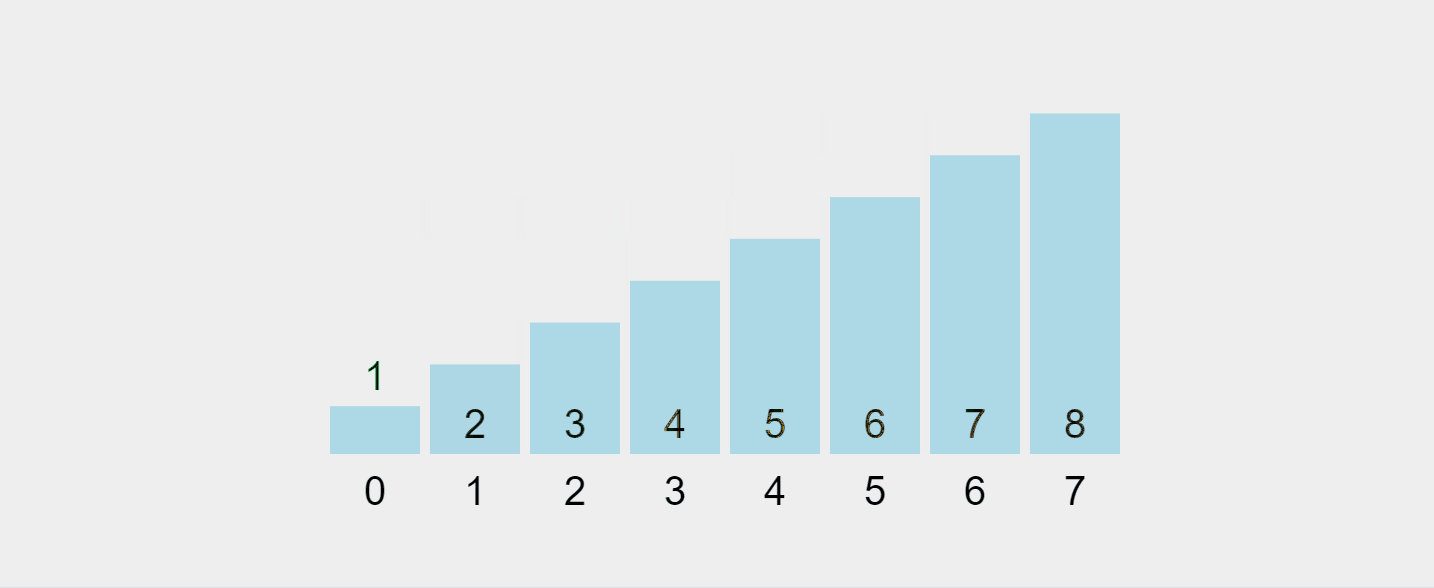
Gif enregistré depuis https://visualgo.net/en/sorting

Implémentation du tri à bulles en JavaScript

Examinons trois implémentations de Bubble Sort en JavaScript, chacune avec des niveaux d'optimisation croissants.

Implémentation de base (v1)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Inner loop: compare adjacent elements
    for (let j = 0; j < list.length - 1; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
      }
    }
  }
  // Return the sorted list
  return list;
}

Cette implémentation de base utilise des boucles imbriquées pour comparer et échanger des éléments adjacents. La boucle externe garantit que nous effectuons suffisamment de passages dans le tableau, tandis que la boucle interne effectue les comparaisons et les échanges.

Implémentation optimisée (v2)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Flag to check if any swaps occurred in this pass
    let swapped = false;
    // Inner loop: compare adjacent elements
    for (let j = 0; j < list.length - 1; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
        // Set the swapped flag to true
        swapped = true;
      }
    }    
    // If no swaps occurred in this pass, the list is sorted
    if (!swapped) {
      break; // Exit the outer loop early
    }
  }
  // Return the sorted list
  return list;
}

Cette version introduit un indicateur d'échange pour vérifier si des échanges ont été effectués lors d'une passe. Si aucun échange ne se produit, la liste est déjà triée et nous pouvons sortir de la boucle plus tôt.

Implémentation la plus optimisée (v3)

function bubbleSort(list) {
  // Outer loop: iterate through the entire list
  for (let i = 0; i < list.length - 1; i++) {
    // Flag to check if any swaps occurred in this pass
    let swapped = false;
    // Inner loop: compare adjacent elements
    // Note: We reduce the upper bound by i in each pass
    for (let j = 0; j < list.length - 1 - i; j++) {
      // If the current element is greater than the next one
      if (list[j] > list[j + 1]) {
        // Swap the elements using destructuring assignment
        [list[j], list[j + 1]] = [list[j + 1], list[j]];
        // Set the swapped flag to true
        swapped = true;
      }
    }    
    // If no swaps occurred in this pass, the list is sorted
    if (!swapped) {
      break; // Exit the outer loop early
    }
  }
  // Return the sorted list
  return list;
}

Cette optimisation finale réduit la portée de la boucle interne de i à chaque passage. En effet, après chaque passage, le plus grand élément non trié « bouillonne » jusqu'à sa position correcte à la fin du tableau.

Analyse de la complexité temporelle et spatiale

Les caractéristiques de performance de Bubble Sort sont les suivantes :

• Complexité temporelle :

  • Meilleur cas : O(n) - lorsque le tableau est déjà trié
  • Cas moyen : O(n^2)
  • Pire des cas : O(n^2) - lorsque le tableau est dans l'ordre inverse

• Complexité spatiale : O(1) - Bubble Sort est un algorithme de tri sur place, ne nécessitant qu'une quantité constante de mémoire supplémentaire.

Comparé à des algorithmes plus avancés comme le tri rapide (moyenne O(n log n)) ou le tri par fusion (O(n log n)), la complexité temporelle quadratique du tri à bulles le rend inefficace pour les grands ensembles de données.

Avantages et inconvénients du tri à bulles

Avantages :

• Simple à comprendre et à mettre en œuvre
• Tri sur place (espace O(1))
• Algorithme de tri stable
• Peut détecter les listes déjà triées

Inconvénients :

• Inefficace pour les grands ensembles de données (O(n^2))
• Mauvaises performances sur des données presque triées
• Opérations d'échange excessives

Quand utiliser le tri à bulles

• Objectifs pédagogiques : Sa simplicité le rend excellent pour enseigner les concepts de base des algorithmes.
• Petits ensembles de données : pour les très petits tableaux, la différence de performances par rapport aux algorithmes complexes peut être négligeable.
• Données presque triées : Avec la version optimisée, elles peuvent être raisonnablement efficaces sur des listes presque triées.
• Environnements de mémoire limitée : sa nature sur place peut être avantageuse dans des scénarios extrêmement limités en mémoire.

Tri des cocktails : une variante améliorée

Cocktail Sort, également connu sous le nom de Cocktail Shake Sort ou Bidirectionnel Bubble Sort, est une version améliorée de Bubble Sort. Il parcourt la liste dans les deux sens, aidant ainsi à déplacer plus efficacement les éléments vers leurs positions correctes.

How Cocktail Sort Works

1. Start with the first element and move towards the end, swapping adjacent elements if they're in the wrong order.
2. When you reach the end, start from the second-to-last element and move towards the beginning, again swapping elements as needed.
3. Repeat this process, narrowing the range of elements to check with each pass, until no swaps are needed.

Cocktail Sort is particularly useful in cases where the array has elements that are initially large at the beginning and small at the end, as it can reduce the total number of passes needed compared to traditional Bubble Sort.

Here's a visualization of Cocktail Sort:

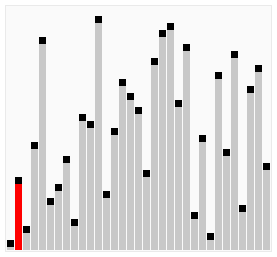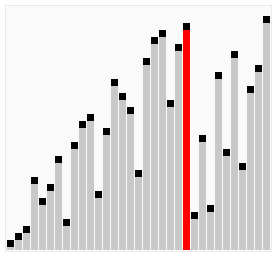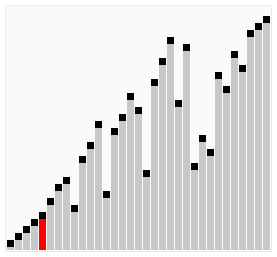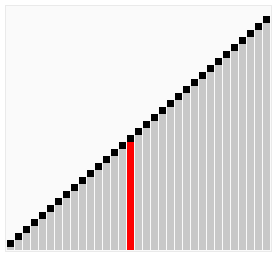
Visual from Wikipedia: https://en.wikipedia.org/wiki/Cocktail_shaker_sort

Cocktail Sort implementation in Javascript

function cocktailSort(list) {
  let swapped;

  // The do...while loop ensures the sorting continues until no swaps are needed
  do {
    // Reset the swapped flag at the beginning of each complete iteration
    swapped = false;

    // First pass: left to right (like standard bubble sort)
    for (let i = 0; i < list.length - 1; i++) {
      // If the current element is greater than the next, swap them
      if (list[i] > list[i + 1]) {
        [list[i], list[i + 1]] = [list[i + 1], list[i]];
        // Mark that a swap occurred
        swapped = true;
      }
    }

    // If no swaps occurred in the first pass, the array is sorted
    if (!swapped) {
      break; // Exit the do...while loop early
    }

    // Reset the swapped flag for the second pass
    swapped = false;

    // Second pass: right to left (this is what makes it "cocktail" sort)
    for (let i = list.length - 2; i >= 0; i--) {
      // If the current element is greater than the next, swap them
      if (list[i] > list[i + 1]) {
        [list[i], list[i + 1]] = [list[i + 1], list[i]];
        // Mark that a swap occurred
        swapped = true;
      }
    }

    // The loop will continue if any swaps occurred in either pass
  } while (swapped);

  // Return the sorted list
  return list;
}

This implementation alternates between forward and backward passes through the list, potentially reducing the number of iterations needed to sort the array.

Practical Applications and Use Cases

While Bubble Sort isn't typically used in production environments for large-scale applications, it can still find use in certain scenarios:

1. Educational tools: It's often used to introduce sorting algorithms and algorithm analysis in computer science education.
2. Embedded systems: In systems with very limited memory, its in-place sorting can be advantageous.
3. Small datasets: For sorting small lists (e.g., less than 50 elements), its simplicity might outweigh the performance benefits of more complex algorithms.
4. Nearly sorted data: If data is known to be almost sorted, an optimized Bubble Sort can be reasonably efficient.
5. Sorting stability requirement: When a stable sort is needed and simplicity is preferred over efficiency, Bubble Sort can be a straightforward choice.

Conclusion

Bubble Sort, despite its inefficiencies with large datasets, offers valuable insights into the world of sorting algorithms and algorithm analysis. Its straightforward approach makes it an excellent teaching tool for beginners in computer science.

Key takeaways are:

• It's simple to understand and implement.
• It has a time complexity of O(n^2), making it inefficient for large datasets.
• It's an in-place and stable sorting algorithm.
• Optimizations can improve its performance, especially for nearly sorted data.
• It's primarily used for educational purposes and in scenarios with very small datasets or limited memory.

While you're unlikely to use Bubble Sort in production code for large-scale applications, the principles behind it are fundamental to many algorithms. The process of optimizing Bubble Sort teaches valuable lessons about algorithm improvement, serving as a stepping stone to more advanced computational problem-solving.

When it comes to algorithms, there's rarely a one-size-fits-all solution. The best algorithm for a given task depends on the specific requirements, constraints, and characteristics of your data. Bubble Sort, with all its limitations, still has its place in this diverse algorithmic ecosystem.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!