Concentrez-vous dessus ! ! Analyse de deux cadres algorithmiques majeurs pour l'inférence causale

1. Cadre général

Les tâches principales peuvent être divisées en trois catégories. La première est la découverte de structures causales, c'est-à-dire l'identification des relations causales entre les variables des données. La seconde est l’estimation des effets causals, c’est-à-dire la déduction des données sur le degré d’influence d’une variable sur une autre variable. Il convient de noter que cet impact ne fait pas référence à la nature relative, mais à la manière dont la valeur ou la distribution d'une autre variable change lorsqu'une variable intervient. La dernière étape consiste à corriger les biais, car dans de nombreuses tâches, divers facteurs peuvent entraîner une distribution différente des échantillons de développement et des échantillons d'application. Dans ce cas, l’inférence causale peut nous aider à corriger les biais.

Ces fonctions conviennent à une variété de scénarios, dont le plus typique est celui de la prise de décision. Grâce à l'inférence causale, nous pouvons comprendre comment les différents utilisateurs réagissent à notre comportement décisionnel. Deuxièmement, dans les scénarios industriels, les processus métiers sont souvent complexes et longs, ce qui entraîne un biais dans les données. Décrire clairement les relations de cause à effet de ces écarts par l’inférence causale peut nous aider à les corriger. En outre, de nombreux scénarios imposent des exigences élevées en matière de robustesse et d’interprétabilité des modèles. On espère que le modèle pourra faire des prédictions basées sur des relations causales, et que l’inférence causale pourra aider à construire des modèles explicatifs plus puissants. Enfin, l’évaluation des effets des résultats de la prise de décision est également importante. L’inférence causale peut aider à mieux analyser les effets réels des stratégies.

Ensuite, nous présenterons deux questions importantes dans l'inférence causale : comment juger si une scène est adaptée à l'inférence causale et les algorithmes typiques de l'inférence causale. Premièrement, il est essentiel de déterminer si un scénario convient à l’application de l’inférence causale. L'inférence causale est généralement utilisée pour résoudre le problème de causalité, c'est-à-dire pour déduire la relation entre cause et effet à travers des données observées. Par conséquent, lors du jugement d'un

2. Évaluation d'un scénario d'application (problème de prise de décision)

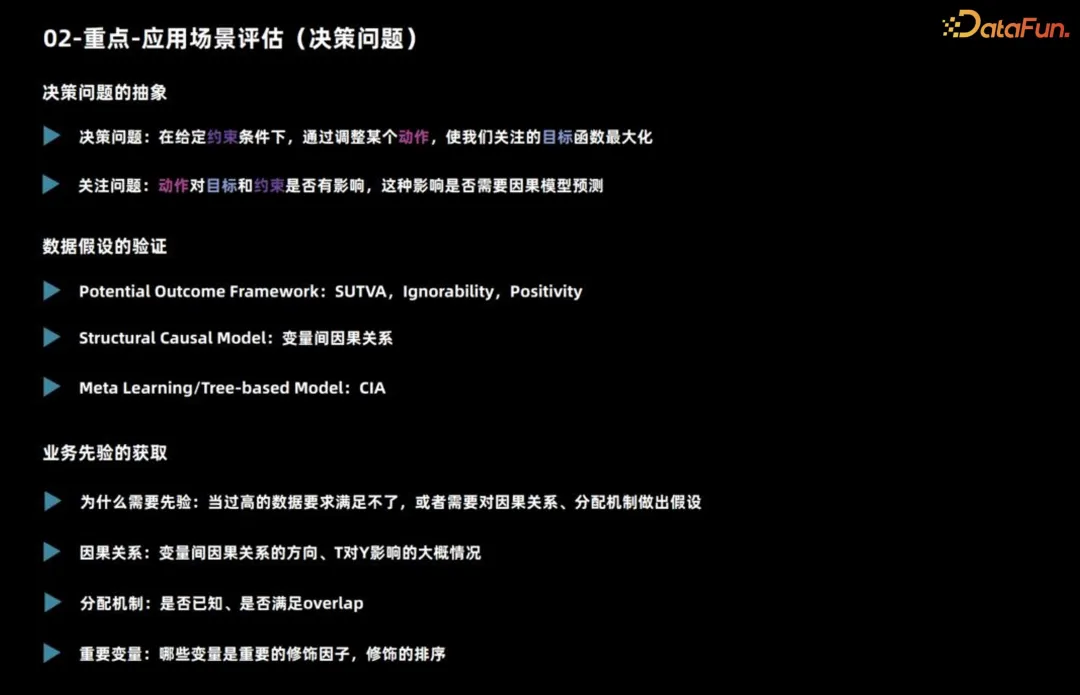
Tout d'abord, nous introduisons l'évaluation d'un scénario d'application pour juger si un scénario est adapté à l'utilisation de l'inférence. implique principalement des problèmes de prise de décision.

Concernant un problème de prise de décision, il faut d'abord clarifier de quoi il s'agit, c'est-à-dire quelle action réaliser sous quelles contraintes pour maximiser quel objectif. Ensuite, vous devez vous demander si cette action a un impact sur les objectifs et les contraintes, et si vous devez utiliser un modèle d'inférence causale pour la prédiction. Par exemple, lors de la commercialisation d'un produit, nous réfléchissons généralement à l'opportunité d'émettre des coupons ou des remises à chaque utilisateur en fonction du budget total. Considérez la maximisation des ventes comme objectif global. S'il n'y a pas de contrainte budgétaire, cela peut affecter les ventes finales, mais tant que vous savez qu'il s'agit d'une stratégie prospective, vous pouvez accorder des réductions à tous les utilisateurs. Dans ce cas, même si l’action décisionnelle a un impact sur la cible, il n’est pas nécessaire d’utiliser un modèle d’inférence causale pour la prédiction.

Ce qui précède est l'analyse de base du problème de prise de décision. De plus, il est nécessaire d'observer si les éléments de données sont satisfaits. Pour créer des modèles causals, différents algorithmes causals ont des exigences différentes en matière de données et d'hypothèses de tâches.

• Le modèle des classes de résultats potentiels repose sur trois hypothèses clés. Premièrement, l'effet causal individuel doit être stable.Par exemple, lors de l'exploration de l'impact de l'émission de coupons sur la probabilité d'achat des utilisateurs, il est nécessaire de s'assurer que le comportement d'un utilisateur n'est pas affecté par d'autres utilisateurs, comme une comparaison de prix hors ligne ou qu'il n'est pas affecté. par des coupons avec différentes réductions. La deuxième hypothèse est que le traitement réel de l'utilisateur et les résultats potentiels sont indépendants compte tenu de la situation caractéristique, ce qui peut être utilisé pour traiter des confusions non observées. La troisième hypothèse concerne le chevauchement, c'est-à-dire que tout type d'utilisateur devrait prendre des décisions différentes, sinon les performances de ce type d'utilisateur sous différentes décisions ne peuvent pas être observées.
• La principale hypothèse à laquelle sont confrontés les modèles causals structurels est la relation causale entre les variables, et ces hypothèses sont souvent difficiles à prouver. Lors de l'utilisation du méta-apprentissage et des méthodes basées sur les arbres, l'hypothèse est généralement celle d'une indépendance conditionnelle, c'est-à-dire que les caractéristiques données, les actions décisionnelles et les résultats potentiels sont indépendants. Cette hypothèse est similaire à l’hypothèse d’indépendance mentionnée précédemment.

Dans les scénarios commerciaux réels, la compréhension des connaissances préalables est cruciale. Tout d’abord, il faut comprendre le mécanisme de distribution des données d’observation réelles, qui constitue la base des décisions précédentes. Lorsque les données les plus précises ne sont pas disponibles, il peut être nécessaire de s’appuyer sur des hypothèses pour tirer des conclusions. Deuxièmement, l’expérience commerciale peut nous guider pour déterminer quelles variables ont un impact significatif sur la distinction des effets causals, ce qui est essentiel pour l’ingénierie des fonctionnalités. Par conséquent, lorsqu'il s'agit d'affaires réelles, en combinaison avec le mécanisme de distribution des données d'observation et de l'expérience commerciale, nous pouvons mieux faire face aux défis et mener efficacement la prise de décision et l'ingénierie des fonctionnalités.

3. Algorithme causal typique

La deuxième question importante est la sélection de l'algorithme d'inférence causale.

Le premier est l'algorithme de découverte de structure causale. L’objectif principal de ces algorithmes est de déterminer les relations causales entre les variables. Les principales idées de recherche peuvent être divisées en trois catégories. Le premier type de méthode consiste à juger sur la base des caractéristiques d’indépendance conditionnelle du réseau de nœuds dans le graphe causal. Une autre approche consiste à définir une fonction de notation pour mesurer la qualité du diagramme de causalité. Par exemple, en définissant une fonction de vraisemblance, un graphe acyclique orienté qui maximise la fonction est recherché et utilisé comme graphe causal. Le troisième type de méthode introduit plus d’informations. Par exemple, supposons que le processus de génération de données réel pour deux variables suit un type n m, un modèle de bruit additif, puis déterminez le sens de causalité entre les deux variables.

L'estimation des effets causals implique une variété d'algorithmes. Voici quelques algorithmes courants :

• La première est la méthode des variables instrumentales, la méthode did et la méthode de contrôle synthétique qui sont souvent évoquées en économétrie. L'idée centrale de la méthode des variables instrumentales est de trouver des variables liées au traitement mais non liées au terme d'erreur aléatoire, c'est-à-dire des variables instrumentales. À l'heure actuelle, la relation entre la variable instrumentale et la variable dépendante n'est pas affectée par la confusion. La prédiction peut être divisée en deux étapes : d'abord, utiliser la variable instrumentale pour prédire la variable de traitement, puis utiliser la variable de traitement prédite pour prédire. la variable dépendante. Le coefficient de régression obtenu est : est l’effet moyen du traitement (ATE). La méthode DID et la loi de contrôle synthétique sont des méthodes conçues pour les données de panel, mais ne seront pas présentées en détail ici.
• Une autre approche courante consiste à utiliser les scores de propension pour estimer les effets causals. Le cœur de cette méthode est de prédire le mécanisme d’allocation caché, tel que la probabilité d’émettre un coupon ou de ne pas émettre de coupon. Si deux utilisateurs ont la même probabilité d’émettre des coupons, mais qu’un utilisateur a effectivement reçu le coupon et l’autre non, alors nous pouvons considérer les deux utilisateurs comme équivalents en termes de mécanisme de distribution, et donc leurs effets peuvent être comparés. Sur cette base, une série de méthodes peuvent être généralisées, notamment les méthodes d'appariement, les méthodes hiérarchiques et les méthodes de pondération.
• Une autre méthode consiste à prédire directement le résultat. Même en présence de facteurs de confusion non observés, les résultats peuvent être directement prédits au moyen d'hypothèses et automatiquement ajustés via le modèle. Cependant, cette approche peut soulever une question : si prédire directement le résultat suffit, le problème disparaît-il ? En fait, ce n’est pas le cas.
• Le quatrième est l'idée de combiner le score de propension et les résultats potentiels, l'utilisation de méthodes d'apprentissage automatique doubles et robustes peut être plus précise. La double robustesse et le double apprentissage automatique offrent une double assurance en combinant deux méthodes, où la précision de chaque partie garantit la fiabilité du résultat final.
• Une autre méthode est le modèle causal structurel, qui construit un modèle basé sur des relations de cause à effet, telles que des diagrammes de cause à effet ou des équations structurées. Cette approche permet l'intervention directe d'une variable pour obtenir un résultat, ainsi que l'inférence contrefactuelle. Cependant, cette approche suppose que nous connaissons déjà les relations causales entre les variables, ce qui constitue souvent une hypothèse luxueuse.
• La méthode d'apprentissage méta est une méthode d'apprentissage importante qui couvre de nombreuses catégories différentes. L’un d’eux est le S-learning, qui traite la méthode de traitement comme une fonctionnalité et l’intègre directement dans le modèle. En ajustant cette fonctionnalité, nous pouvons observer des changements dans les résultats selon différentes méthodes de traitement. Cette approche est parfois appelée apprenant à modèle unique car nous construisons un modèle pour chacun des groupes expérimentaux et témoins, puis modifions les caractéristiques pour observer les résultats. Une autre méthode est le X-learning, dont le processus est similaire au S-learning, mais prend en compte en plus l'étape de validation croisée pour évaluer plus précisément les performances du modèle.
• La méthode arborescente est une méthode intuitive et simple qui divise l'échantillon en construisant une structure arborescente pour maximiser la différence d'effets causals sur les nœuds gauche et droit. Cependant, cette méthode est sujette au surajustement, c'est pourquoi, dans la pratique, des méthodes telles que les forêts aléatoires sont souvent utilisées pour réduire le risque de surajustement. L'utilisation de la méthode de boosting peut augmenter le défi car il est plus facile de filtrer certaines informations. Des modèles plus complexes doivent donc être conçus pour éviter la perte d'informations lors de son utilisation. Les méthodes de méta-apprentissage et les algorithmes basés sur des arbres sont également souvent appelés modèles Uplift.
• La représentation causale est l'un des domaines qui a obtenu certains résultats dans le monde universitaire ces dernières années. Cette méthode s’efforce de découpler les différents modules et de séparer les facteurs d’influence pour identifier plus précisément les facteurs de confusion. En analysant les facteurs qui affectent la variable dépendante y et la variable de traitement (traitement), nous pouvons identifier les facteurs de confusion qui peuvent affecter y et le traitement. Ces facteurs sont appelés facteurs de confusion. Cette méthode devrait améliorer l’effet d’apprentissage de bout en bout du modèle. Prenez par exemple le score de propension, qui fait souvent un excellent travail pour gérer les facteurs de confusion. Cependant, une précision excessive des scores de propension s’avère parfois défavorable. Sous le même score de propension, il peut y avoir des situations dans lesquelles l'hypothèse de chevauchement ne peut pas être satisfaite, car le score de propension peut contenir certaines informations liées aux facteurs de confusion mais n'affectant pas y. Lorsque le modèle apprend avec trop de précision, cela peut entraîner des erreurs plus importantes lors de l'appariement pondéré ou du traitement hiérarchique. Ces erreurs ne sont pas réellement causées par des facteurs de confusion et ne doivent donc pas être prises en compte. Les méthodes d’apprentissage de la représentation causale offrent un moyen de résoudre ce problème et peuvent gérer plus efficacement l’identification et l’analyse des relations causales.

4. Difficultés dans la mise en œuvre réelle de l'inférence causale

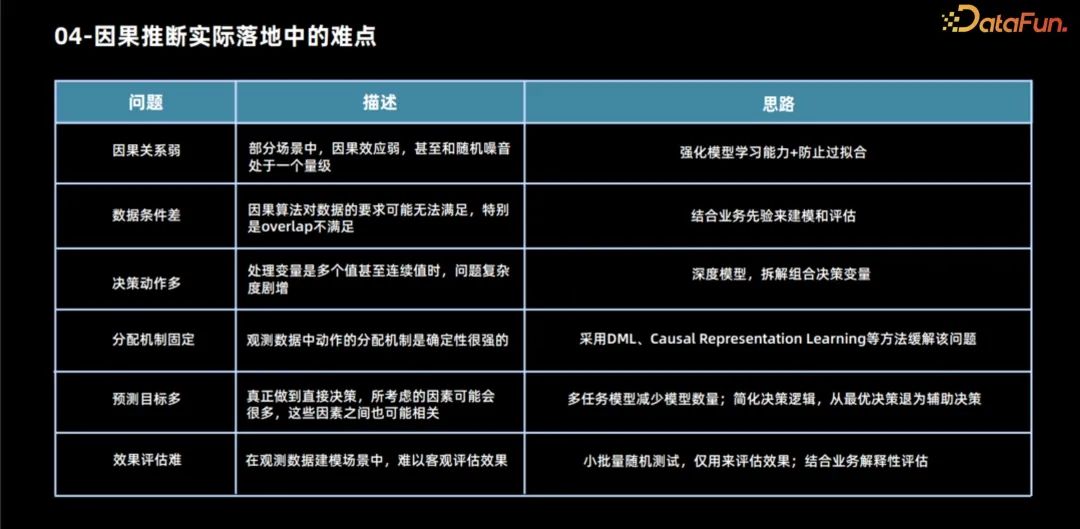
L'inférence causale est confrontée à de nombreux défis dans les applications pratiques.

• Affaiblissement de la relation causale. Dans de nombreux scénarios, les relations causales sont souvent du même ordre que les fluctuations aléatoires du bruit, ce qui représente un énorme défi pour les efforts de modélisation. Dans ce cas, les bénéfices de la modélisation sont relativement faibles car la relation causale elle-même n’est pas évidente. Cependant, même si la modélisation est nécessaire, des modèles dotés de capacités d’apprentissage plus fortes seront nécessaires pour capturer avec précision cette relation causale affaiblie. Dans le même temps, une attention particulière doit être accordée au problème du surajustement, car les modèles dotés de fortes capacités d’apprentissage peuvent être plus sensibles au bruit, ce qui entraîne un surajustement des données.
• Le deuxième problème courant concerne les conditions de données insuffisantes. La portée de ce problème est relativement large, principalement parce que les hypothèses algorithmiques que nous utilisons présentent de nombreuses lacunes, en particulier lorsque nous utilisons des données d'observation pour la modélisation, nos hypothèses peuvent ne pas être complètement vraies. Les problèmes les plus courants incluent le fait que l'hypothèse de chevauchement peut ne pas être satisfaite et que notre mécanisme d'allocation peut manquer de caractère aléatoire. Un problème plus grave est que nous ne disposons même pas de suffisamment de données de tests aléatoires, ce qui rend difficile l’évaluation objective des performances du modèle. Dans ce cas, si nous insistons toujours sur la modélisation et que les performances du modèle sont meilleures que la règle annuelle, nous pouvons utiliser une certaine expérience commerciale pour évaluer si la décision du modèle est raisonnable. D’un point de vue commercial, il n’existe pas de solution théorique particulièrement efficace aux situations dans lesquelles certaines hypothèses ne sont pas valables, comme les facteurs de confusion non observés. Cependant, si vous devez utiliser un modèle, vous pouvez essayer d’effectuer des simulations aléatoires à petite échelle basées sur l’entreprise. expérience ou tests pour évaluer la direction et l’ampleur de l’influence des facteurs de confusion. Dans le même temps, en tenant compte de ces facteurs dans le modèle, pour les situations où l'hypothèse de chevauchement n'est pas remplie, bien qu'il s'agisse du quatrième problème de notre énumération plus tard, nous en discuterons ensemble ici. Nous pouvons utiliser certains algorithmes pour en exclure certains. mécanismes d’allocation. facteurs non confondants, c’est-à-dire que ce problème est atténué grâce à l’apprentissage de la représentation causale.
• Face à cette complexité, les actions décisionnelles sont particulièrement importantes. De nombreux modèles existants se concentrent sur la résolution de problèmes binaires. Cependant, lorsque plusieurs solutions de traitement sont impliquées, la manière d'allouer les ressources devient un problème plus complexe. Pour relever ce défi, nous pouvons décomposer plusieurs solutions de traitement en sous-problèmes dans différents domaines. De plus, en utilisant des méthodes d’apprentissage profond, nous pouvons traiter les schémas de traitement comme des caractéristiques et supposer qu’il existe une certaine relation fonctionnelle entre les schémas de traitement successifs et les résultats. En optimisant les paramètres de ces fonctions, les problèmes de décision continus peuvent être mieux résolus, mais cela introduit également des hypothèses supplémentaires, telles que des problèmes de chevauchement.
• Le mécanisme de distribution est fixe. Voir l'analyse ci-dessus.
• Un autre problème courant est d'avoir beaucoup de prédictions de cibles. Dans certains cas, les prédictions des cibles sont affectées par plusieurs facteurs, eux-mêmes associés aux options de traitement. Afin de résoudre ce problème, nous pouvons utiliser une méthode d'apprentissage multitâche. Bien qu'il puisse être difficile de traiter directement des problèmes de rôle complexes, nous pouvons simplifier le problème et prédire uniquement les indicateurs les plus critiques affectés par le plan de traitement, en fournissant progressivement des informations. une référence pour la prise de décision.
• Enfin, le coût des tests aléatoires dans certains scénarios est plus élevé et le cycle de récupération des effets est plus long. Il est particulièrement important d’évaluer pleinement les performances du modèle avant sa mise en ligne. Dans ce cas, des tests randomisés à petite échelle peuvent être utilisés pour évaluer l’efficacité. Bien que l’ensemble d’échantillons requis pour évaluer le modèle soit beaucoup plus petit que l’ensemble d’échantillons pour la modélisation, si même des tests aléatoires à petite échelle ne sont pas possibles, nous ne pourrons peut-être juger du caractère raisonnable des résultats de la décision du modèle que grâce à l’interprétabilité commerciale.

5. Cas - Modèle de prise de décision de limite de crédit de JD Technology

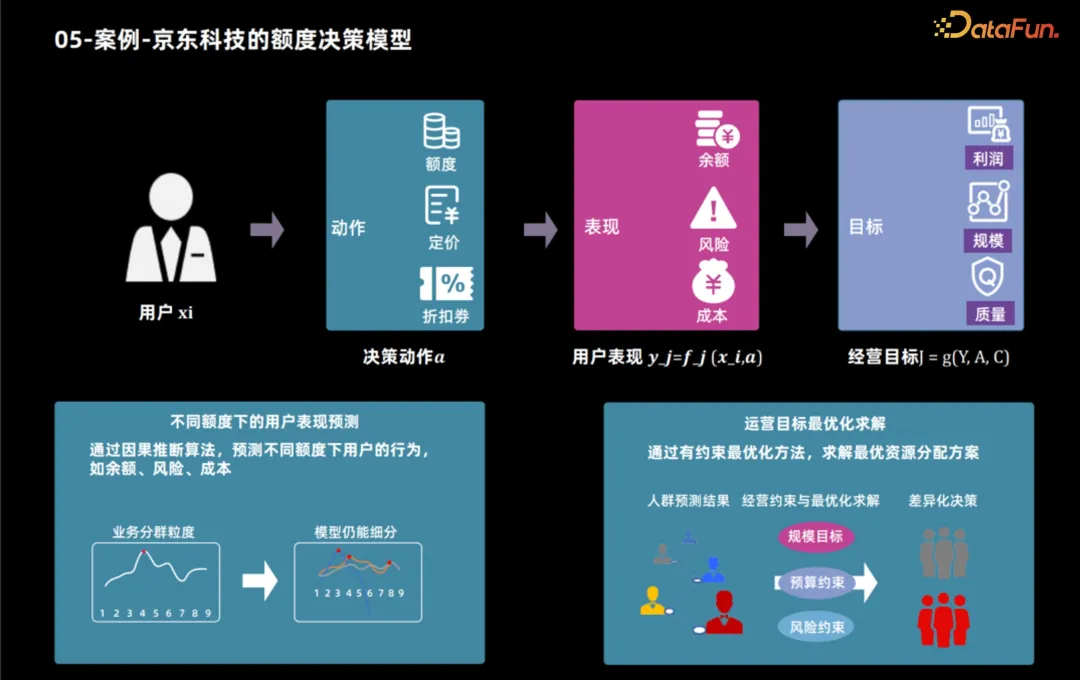
Ensuite, nous prendrons l'application auxiliaire de JD Technology utilisant la technologie d'inférence causale pour formuler des produits de crédit à titre d'exemple pour montrer comment utiliser la technologie d'inférence causale pour formuler des produits de crédit. Les caractéristiques des utilisateurs et les objectifs commerciaux déterminent la limite de crédit optimale. Une fois les objectifs commerciaux déterminés, ces objectifs peuvent généralement être décomposés en indicateurs de performance des utilisateurs, tels que l'utilisation des produits et le comportement d'emprunt des utilisateurs. En analysant ces indicateurs, des objectifs commerciaux tels que le profit et l'échelle peuvent être calculés. Par conséquent, le processus décisionnel en matière de limite de crédit est divisé en deux étapes : premièrement, utiliser la technologie d'inférence causale pour prédire les performances de l'utilisateur sous différentes limites de crédit, puis utiliser diverses méthodes pour déterminer la limite de crédit optimale pour chaque utilisateur en fonction de ces performances et objectifs opérationnels.

6. Développement futur

Nous serons confrontés à une série de défis et d'opportunités dans le développement futur.

Tout d'abord, compte tenu des lacunes des modèles causals actuels, les milieux universitaires estiment généralement que des modèles à grande échelle sont nécessaires pour gérer des relations non linéaires plus complexes. Les modèles causals ne traitent généralement que des données bidimensionnelles, et la plupart des structures de modèles sont relativement simples. Les futures orientations de recherche pourraient donc inclure cette question.

Deuxièmement, les chercheurs ont proposé le concept d'apprentissage des représentations causales, soulignant l'importance du découplage et des idées modulaires dans l'apprentissage des représentations. En comprenant le processus de génération de données d’un point de vue causal, les modèles construits sur la base de lois du monde réel auront probablement de meilleures capacités de transfert et de généralisation.

Enfin, les chercheurs ont souligné que les hypothèses actuelles sont trop fortes et ne peuvent pas répondre aux besoins réels dans de nombreux cas, de sorte que différents modèles doivent être adoptés pour différents scénarios. Cela se traduit également par un seuil très élevé pour la mise en œuvre du modèle. Par conséquent, il est très utile de trouver un algorithme d’huile de serpent polyvalent.