Google blog released new research to solve the minimum cut problem of undirected graphs.
In 1996, American computer scientist David R Karger and other researchers proposed a new approach to the minimum cut problem in the paper "A new approach to the minimum cut problem" The surprisingly random algorithm Karger's algorithm is very important in theoretical computer science and is especially suitable for approximate minimum cut problems on large-scale graphs.
Karger's algorithm can find a minimum cut point in a graph with time O (m log^3n). They call this time nearly linear time, which means Linearly multiplied by a polylog factor.
In a blog just updated by Google, they introduced a previously published paper "Deterministic Near-Linear Time Minimum Cut in Weighted Graphs", and the research obtained ACM-SIAM SODA24 Best Paper Award. The article details a new algorithm that runs in almost linear time (rather than near linear time). This algorithm is deterministic and can reliably find the correct minimum cut. It improves the previous algorithm that may not be guaranteed to be correct or only applicable to Algorithms for simple graphs. Arguably this is the biggest discovery since Karger's famous randomization algorithm.
-
Paper address: https://arxiv.org/pdf/2401.05627.pdf
-
Paper Title: Deterministic Near-Linear Time Minimum Cut in Weighted Graphs
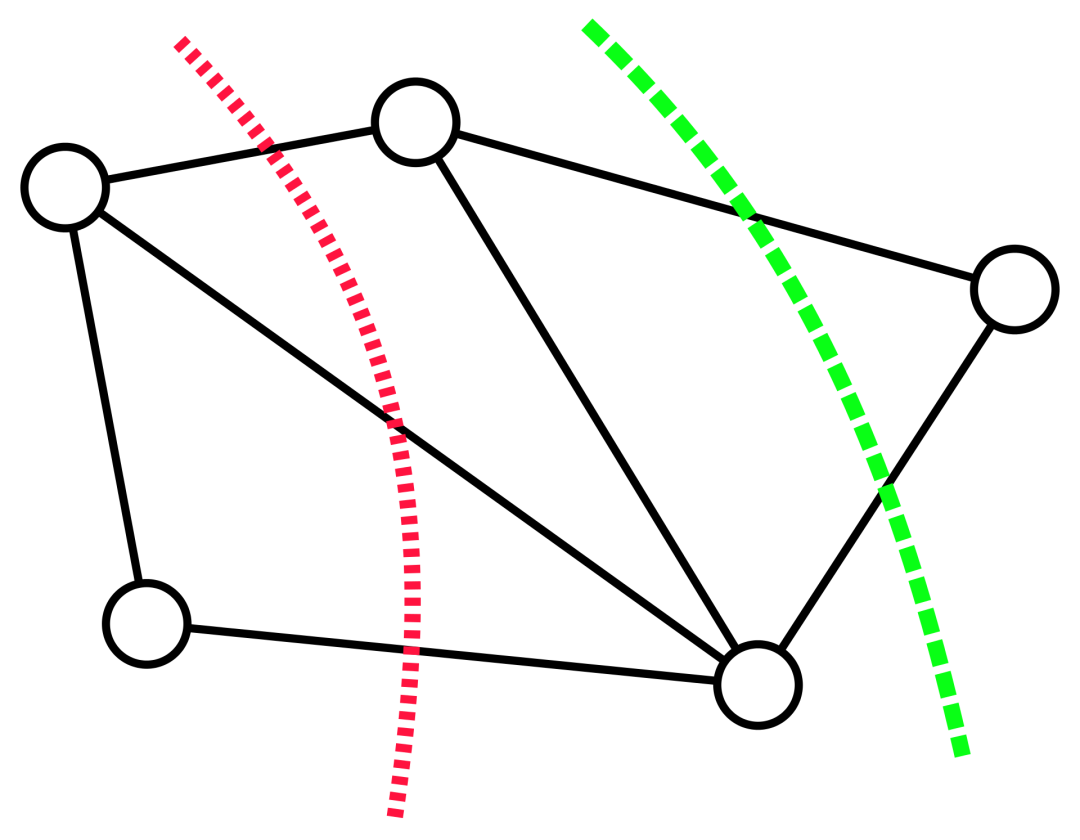
Note: The minimum cut problem (often called minimum cut) is about graph connectivity The basic structural question, which generally focuses on what is the simplest way to disconnect the network? In graph theory, the set of edges that can make a network flow graph no longer connected (that is, divided into two subgraphs) by removing all the edges is called a cut of the graph, and the smallest cut on a graph is called a minimum cut.
## A minimal cut of a graph (containing two edges).
Regarding the minimum cut problem, Karger In 1996, he pioneered a nearly linear time random algorithm that can find the minimum cut with a high probability. This work also gave a key insight that there is a smaller graph, which is in All cut sizes are largely preserved.
This finding is useful because slower algorithms can be run using smaller graphs as input, and slower running times (for smaller graphs in terms of size) can still be close to linear with the size of the original (larger) graph.
#In fact, many structural discoveries about the minimum cut problem are carried out along this direction.
Google does this, starting from a graph G with n nodes, and then based on the paper "Randomized Approximation Schemes for Cuts and Flows in Capacitated Graphs" (authored by Benzur The cut-preserving sparsification method proposed by , Karger proved that it is possible to construct a sparse weighted graph G' with fewer edges, and on this graph, the size of almost all cuts is roughly the same as the size of the corresponding cuts in the original graph G.
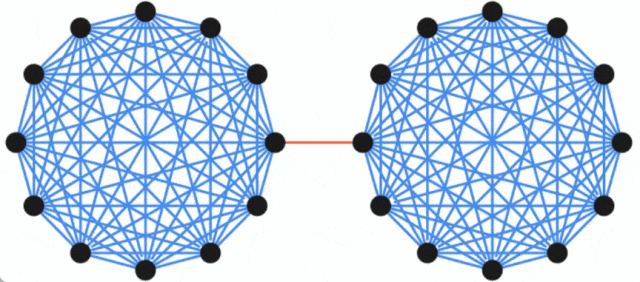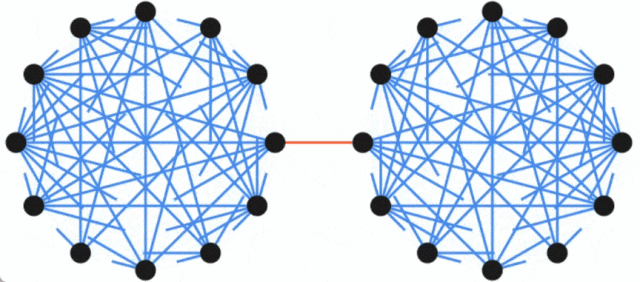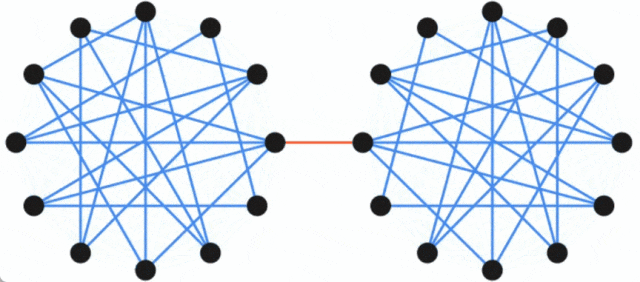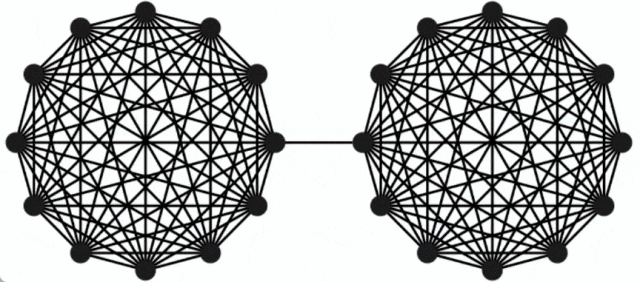
This concept can be illustrated by the following example: the original graph consists of two complete graphs connected by a single edge, while the sparsified graph has fewer edges, but Edges are weighted more heavily, while the size of all cuts is roughly preserved.
To construct this sparser graph, Benzur and Karger adopted the method of independently sampling edges. In this method, each edge in the graph G has a certain probability of being included in the graph G', and its weight in G' will be amplified according to the inverse of the sampling probability (for example, if an edge's original weight is 1 The edge is included with a probability of 10%, then its weight is adjusted to 10). It turns out that this very simple (almost linear time) approach can construct cut-preserving graph sparsifications with a high probability of success.
However, the Karger algorithm is a Monte Carlo algorithm, that is, the output may be incorrect with a small probability, and there is no There are known methods to determine whether the output is correct.
# Therefore, researchers have been working hard to explore ways to solve the open problem of near-linear time deterministic algorithms. Since the construction of cut-preserving graph sparsification is the only stochastic component in Karger's algorithm, one approach is to find a deterministic construction of the sparsification in near-linear time (also called derandomization).
In 2015, Kawarabayashi and Thorup achieved an important milestone - finding a graph for a simple graph (that is, there is at most one edge between each pair of nodes and all edge weights are equal to 1 graph) of a deterministic near-linear time algorithm.
The study leads to a key idea, that is, there is some connection between the minimum cut and another important graph structure (called "low-conductance cut"). This connection was crucial to later derandomizing Karger's algorithm on general edge-weighted graphs, and helped Google derive its new algorithm.
Alignment of minimum cut and low-conductance cut
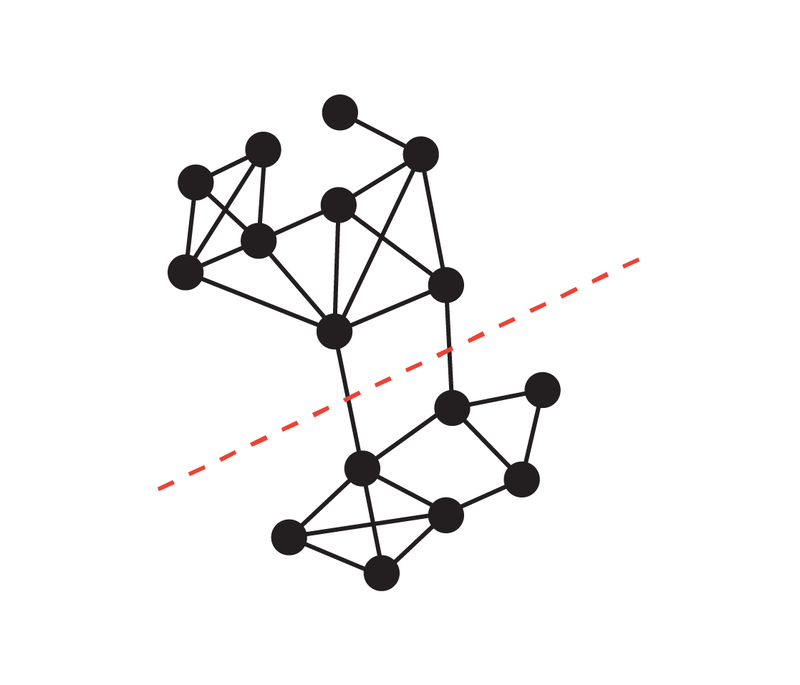
Conductance of graph cut S Defined as the ratio of the cut size of S to the volume of S (assuming that S is the smaller volume side of the cut and non-empty), where the volume of S is the degree of the node in S.
# A low-conductance cut S intuitively captures the bottleneck in the network, since only a small number of edges (relative to its volume) connect S to the rest of the graph. The conductance of a graph is defined as the minimum conductance for any cut in the graph, and graphs with large conductance (also called extended graphs) are said to be well connected because there are no bottlenecks inside.
## This red dotted line indicates that the CUT size is 2, and the smaller side (bottom) volume is 24, so the confptance is 1/12, this It is also the conductance of the graph.
Kawayabarashi and Thorup observed that in simple graphs with large minimum node degrees, any nontrivial (i.e., having at least two nodes on either side ) minimum cut must have low conductance. Based on this observation, if the graph can be partitioned into well-connected clusters, then the partitioning must be consistent with every nontrivial minimal cut, since every cluster must lie exactly on one side of every cut. Then, each cluster is shrunk to a node and a smaller graph is processed where all non-trivial minimum cuts of the original graph are intact.
However, for weighted graphs, the above observation no longer holds, and the same partitioning used in the simple graph case may not be exactly consistent with non-trivial minimum cuts.
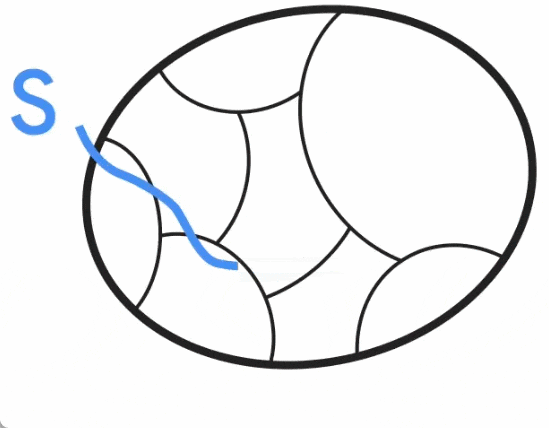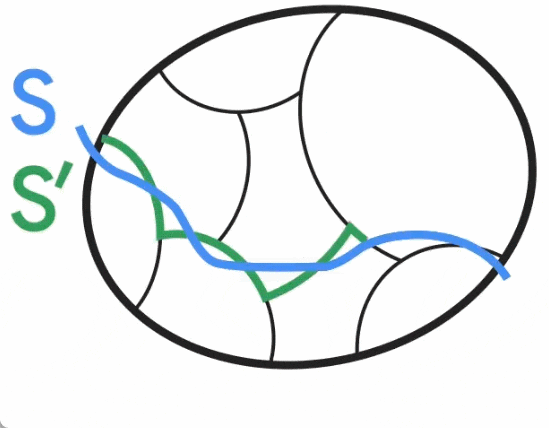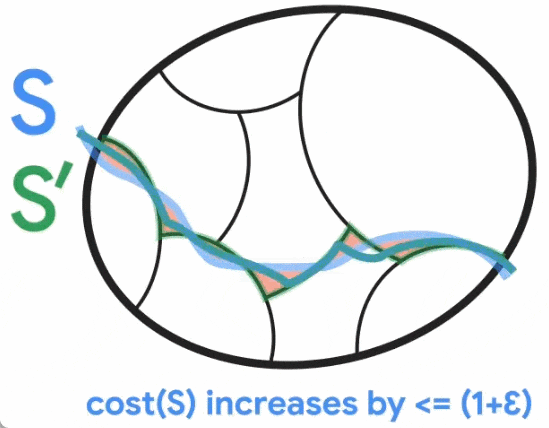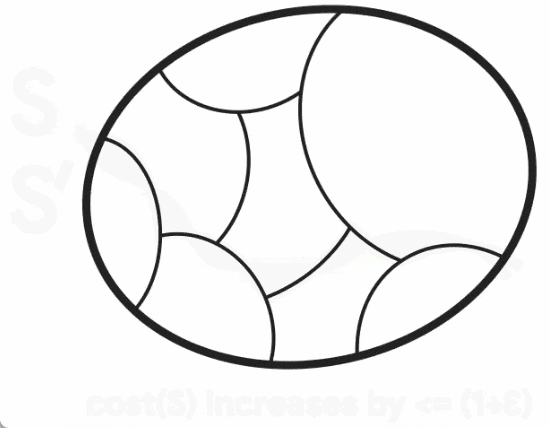
As shown in the figure below, Jason Li observed in 2021 that this division is still roughly consistent with non-trivial minimum cuts. In particular, for a non-trivial minimal cut S, there is a cut S' that is similar to S such that S' is consistent with the cluster. Jason Li further observed that this property of partitioning can be exploited to effectively de-randomize the construction of cut-preserving graph sparsity.
#The new algorithm designed by Google aims to construct a partition to formulate the use case of minimum cut. The Google study is more precise and faster than the more general, off-the-shelf methods Jason Li used in previous work. The new research optimizes the running time while ensuring accuracy, and finally achieves a near-linear time deterministic algorithm for the minimum cut problem.
Reference link: https://research.google/blog/solving-the-minimum-cut-problem-for-undirected-graphs/
The above is the detailed content of A new breakthrough was made in the minimum cut problem of undirected graphs, and Google research won the SODA 2024 Best Paper Award. For more information, please follow other related articles on the PHP Chinese website!