Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process

After being “endorsed” by GPT-4, Copilot was also ambushed by Terence Tao.

He bluntly said that when programming, Copilot can directly predict what he will do next.

With Copilot, research has become more convenient, and Tao Zhexuan also used it to assist him in completing his latest research results.

Tao Zhexuan said that this part of the paper actually only has one page.

But to complete this one-page proof, he wrote more than 200 lines of code, using the newly learned programming language Lean4.

The GitHub page of Tao Zhexuan’s public code shows that Copilot has increased the speed of writing code by more than half.

Tao Zhexuan said that the reason why he chose Lean4 was because of its "rewriting strategy", which is to perform targeted partial replacement of a long expression.

For example, if a complex function f(x) is defined, when we want to enter the expression of f(114514), we can directly "rewrite" x into 114514 using code.

Tao Zhexuan said that this feature is not too convenient compared to LaTeX which requires repeated input of formulas.

So what new results has Tao Zhexuan’s “one-page proof” brought us this time?

One-page proof of new inequalities

This paper talks about issues related to MacLaughlin's inequality.

McLaughlin's inequality is a classic inequality in mathematics. It is derived based on the law that "the arithmetic mean of non-negative real numbers is greater than or equal to the geometric mean". It can be expressed as:

Assume y₁…y_nis a non-negative real number. For k=1…n, the mean S_kis defined as (the number of terms whose denominator is the numerator):

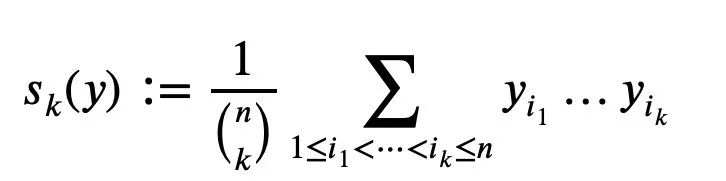
#It occurs as the normalized coefficient of a polynomial of degree n with roots.

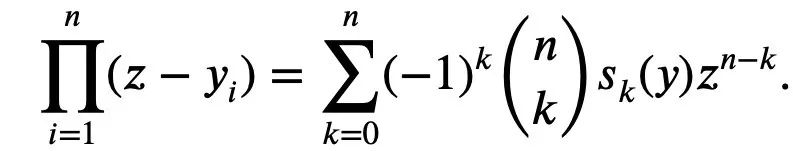
(Remember this formula, we call it Formula 1)

Then MacLaughlin’s inequality can be expressed as:

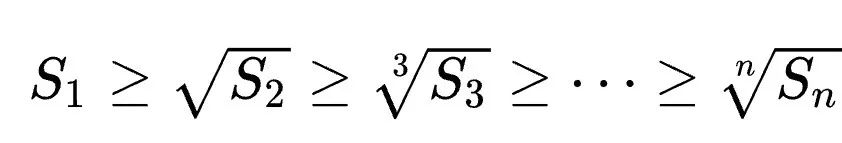
Among them, the equal sign holds true if and only if all y_iare equal.

In calculus, there is also a classic Newton's inequality:

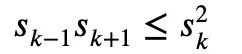
For any 1≤k n are all non-negative, Newton's inequality can simply describe Maclaurin's inequality:

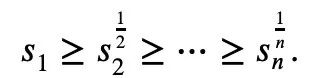
But if this restriction is not added, negative numbers are allowed With the existence of terms, Maclaurin's inequality cannot be expressed using Newton's inequality.

So for the situation where negative terms may exist in Newton's inequalities, Tao Zhexuan proposed a new set of inequality variants:

For any r>0 and 1≤ℓ≤n, there must be a formula 2 or Equation 3 is established.

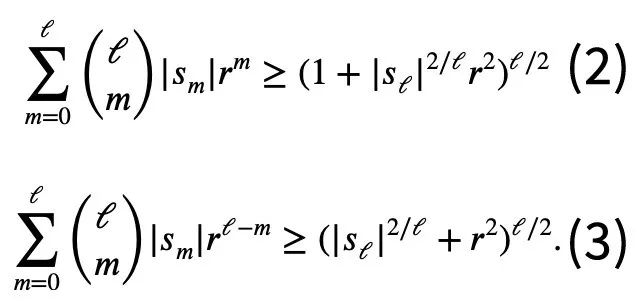
This is what Terence Tao is trying to prove on this page. The specific proof process is as follows:

We might as well construct a polynomial about the complex variable z P(z):

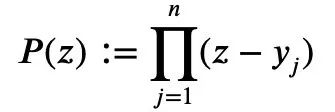
From the previous equation 1 and the triangle inequality, we can get:

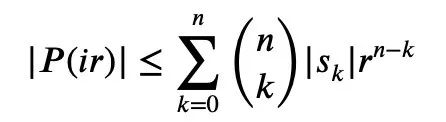
So we only need to establish the lower bound:

## Take the absolute value of P(z) and then take the logarithm to get:

Since for any real number t, t ↦ log(e

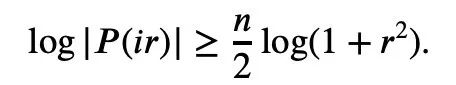
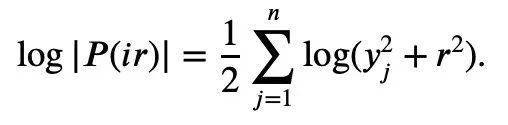
t^{a) is convex and a>0, we can get the inequality:}

When a=r

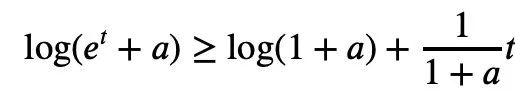
2^{, t=2log y}j_{, it can be concluded:}

The above is the proof given by Terence Tao process, however, when the normalized |S

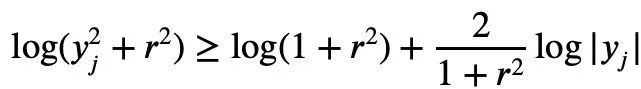
n_{|=1, the following formula holds:}

Next step: Create a refined version

In addition to the "one-page proof" mentioned this time, Tao Zhexuan's paper also proposed another new theorem, that is, for any 1 ≤ k ≤ ℓ≤ n.:

In a blog post, Terence Tao revealed that his next step is to propose a refined version of this inequality.

Tao Zhexuan said that the process of proof will be very simple "just like practice" and can be done with calculus.

However, he also mentioned that there will be a small difficulty because this part of the argument uses asymptotic symbols.

Let us wait and see what the new conclusion will be.

One More Thing

Tao Zhexuan is a loyal fan of AI tools. Copilot, GPT-4, and some other auxiliary tools have been recommended by him.

This time, he also put forward new expectations for the development of large models, hoping that one day the model can directly generate inequality variants.

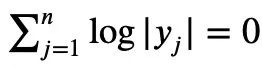
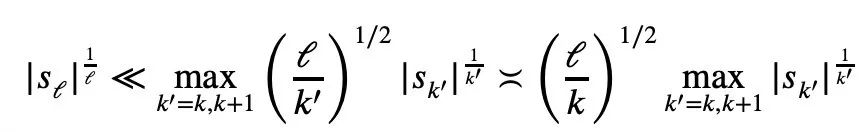
Paper address:https://arxiv.org/abs/2310.05328

The above is the detailed content of Terence Tao's Crazy Amway Copilot: It helped me complete a one-page proof and even guessed my subsequent process. For more information, please follow other related articles on the PHP Chinese website!