Have you ever made a Mobius strip yourself?
The Möbius strip is a peculiar mathematical structure. It is actually very simple to construct such a beautiful single-sided surface, even a child can easily complete it. You just need to take a piece of paper tape, twist it once, and tape the two ends together. However, such an easy-to-make Möbius strip has complex properties that have long attracted the interest of mathematicians. Recently, researchers have been troubled by a seemingly simple question, that is, what is the minimum length of paper tape required to make a Möbius strip? Richard Evan Schwartz of Brown University said that this problem is not solved for Möbius strips because they are "embedded" rather than "immersed," meaning they do not penetrate each other or intersect themselves. A Möbius strip is actually a hologram, a figure projected into three-dimensional space: for an "immersed" Möbius strip, multiple layers of strips can overlap each other, a bit like a ghost passing through a wall; for an "embedded" Möbius strip 's, there is no such overlap.  In 1977, mathematicians Charles Sidney Weaver and Benjamin Rigler Halpern asked this problem about minimum dimensions and pointed out that if the Möbius strip is allowed to self-intersect, then this The problem is simple. The remaining problem, then, is to determine how much space is needed to avoid self-intersection. Halpern and Weaver proposed a minimum size, but they were unable to prove the idea, so it became known as the Halpern-Weaver conjecture. Schwartz first learned about the problem four years ago and became fascinated by it. Now, his interest has turned into new fruits. Paper address: https://arxiv.org/pdf/2308.12641.pdfHe will be in 2023 The Halpern-Weaver conjecture was proven in a preprint paper posted on arXiv.org on August 24. He demonstrated that "embedded" Möbius strips made of paper could only be constructed with aspect ratios greater than
In 1977, mathematicians Charles Sidney Weaver and Benjamin Rigler Halpern asked this problem about minimum dimensions and pointed out that if the Möbius strip is allowed to self-intersect, then this The problem is simple. The remaining problem, then, is to determine how much space is needed to avoid self-intersection. Halpern and Weaver proposed a minimum size, but they were unable to prove the idea, so it became known as the Halpern-Weaver conjecture. Schwartz first learned about the problem four years ago and became fascinated by it. Now, his interest has turned into new fruits. Paper address: https://arxiv.org/pdf/2308.12641.pdfHe will be in 2023 The Halpern-Weaver conjecture was proven in a preprint paper posted on arXiv.org on August 24. He demonstrated that "embedded" Möbius strips made of paper could only be constructed with aspect ratios greater than 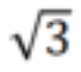 . For example, if the strap length is 1 cm, its width must be greater than
. For example, if the strap length is 1 cm, its width must be greater than  cm. Solving this puzzle requires mathematical creativity. When one takes the standard approach to solving this type of problem, it is difficult to distinguish between self-intersecting and non-self-intersecting surfaces through formulas. It takes Schwartz's geometric vision to overcome this difficulty, but this is rare. In Schwartz's proof, he managed to break the problem down into tractable parts, each of which essentially required only basic knowledge of geometry to solve. In fact, Schwartz tried other strategies on and off for several years before finding one that worked. He recently decided to revisit the problem because he had always felt that the method he used in a 2021 paper should be valid. Obviously, his intuition was correct. When he revisited the problem, he noticed an error in the lemma involving T-charts in the previous paper. By correcting this error, Schwartz quickly and easily proved the Halpern-Weaver conjecture. Schwartz himself says that if not for that mistake, he would have solved the problem three years ago.
cm. Solving this puzzle requires mathematical creativity. When one takes the standard approach to solving this type of problem, it is difficult to distinguish between self-intersecting and non-self-intersecting surfaces through formulas. It takes Schwartz's geometric vision to overcome this difficulty, but this is rare. In Schwartz's proof, he managed to break the problem down into tractable parts, each of which essentially required only basic knowledge of geometry to solve. In fact, Schwartz tried other strategies on and off for several years before finding one that worked. He recently decided to revisit the problem because he had always felt that the method he used in a 2021 paper should be valid. Obviously, his intuition was correct. When he revisited the problem, he noticed an error in the lemma involving T-charts in the previous paper. By correcting this error, Schwartz quickly and easily proved the Halpern-Weaver conjecture. Schwartz himself says that if not for that mistake, he would have solved the problem three years ago. 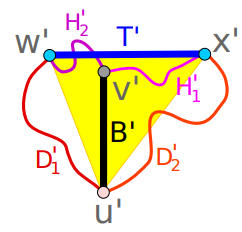 ## is the key. This lemma is based on a basic idea: some straight lines on a Möbius strip are called ruled surfaces. Schwartz pointed out that a strip of paper in space, even if it is in some complicated position, still has a straight line running through it at every point. You can imagine drawing these straight lines so that they cross the Möbius strip and Both ends touch the border.In previous work, Schwartz determined that two straight lines parallel to each other and in the same plane formed a Möbius strip in each T pattern. He points out that it is not obvious that these things exist and that they need to be proven, which is the first part of proving the lemma. The next step is to set up and solve the optimization problem, which requires cutting a Möbius strip at an angle along a line segment extending the width of the strip, and getting the final shape. Schwartz mistakenly concluded in his 2021 paper that the shape was a parallelogram. This summer, Schwartz decided to try a different tack. He started trying to flatten the Möbius strip. If it could be shown that they could be pressed into a flat surface, this complex problem would be reduced to a more tractable flat surface problem. In an experiment, Schwartz cut open a Möbius strip and realized that it was not a parallelogram but a trapezoid. Finally, the 50-year-old question has been answered. It takes courage to try to solve a long-standing problem, and this is Schwartz's strength in mathematics: he likes to work on problems that seem relatively easy but are actually difficult. He will see problems that previous researchers have not noticed. Reference link: https://www.scientificamerican.com/article/mathematicians-solve-50-year- old-moebius-strip-puzzle1/
## is the key. This lemma is based on a basic idea: some straight lines on a Möbius strip are called ruled surfaces. Schwartz pointed out that a strip of paper in space, even if it is in some complicated position, still has a straight line running through it at every point. You can imagine drawing these straight lines so that they cross the Möbius strip and Both ends touch the border.In previous work, Schwartz determined that two straight lines parallel to each other and in the same plane formed a Möbius strip in each T pattern. He points out that it is not obvious that these things exist and that they need to be proven, which is the first part of proving the lemma. The next step is to set up and solve the optimization problem, which requires cutting a Möbius strip at an angle along a line segment extending the width of the strip, and getting the final shape. Schwartz mistakenly concluded in his 2021 paper that the shape was a parallelogram. This summer, Schwartz decided to try a different tack. He started trying to flatten the Möbius strip. If it could be shown that they could be pressed into a flat surface, this complex problem would be reduced to a more tractable flat surface problem. In an experiment, Schwartz cut open a Möbius strip and realized that it was not a parallelogram but a trapezoid. Finally, the 50-year-old question has been answered. It takes courage to try to solve a long-standing problem, and this is Schwartz's strength in mathematics: he likes to work on problems that seem relatively easy but are actually difficult. He will see problems that previous researchers have not noticed. Reference link: https://www.scientificamerican.com/article/mathematicians-solve-50-year- old-moebius-strip-puzzle1/The above is the detailed content of What is the minimum length of paper tape required to make a Möbius strip? 50-year-old mystery solved. For more information, please follow other related articles on the PHP Chinese website!



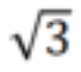 . For example, if the strap length is 1 cm, its width must be greater than
. For example, if the strap length is 1 cm, its width must be greater than  cm.
cm. 




