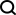Sum sequence 1^2 + 3^2 + 5^2 + . . . + (2*n – 1)^2

A series is a group of numbers that share some common characteristics that each number follows. These mathematical sequences are defined based on some mathematical logic, such as each number increasing by the same interval (arithmetic sequence), each number increasing by the same multiple (geometric sequence), and many other patterns.
To find the sum of a series, we need to evaluate the series and develop a general formula for it. But there is no common statement in this series, so we have to take the classic approach by adding each number of the series to a sum variable.
Let's take an example, this will make the logic clearer:
Sum the series up to the 7th term
sum(7) = 12 22 32 42 52 62 72 = 455
Example
#include <stdio.h>
int main() {
int i, n, sum=0;
n=17 ;
for ( i = 1; i <= n; i++) {
sum = sum + (2 * i - 1) * (2 * i - 1);
}
printf("The sum of series upto %d is %d", n, sum);
}Output
The sum of series upto 17 is 6545
The above is the detailed content of Sum sequence 1^2 + 3^2 + 5^2 + . . . + (2*n – 1)^2. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover