Physical Deep Learning with Biologically Inspired Training Methods: A Gradient-Free Approach to Physical Hardware

The growing demand for artificial intelligence has driven research into unconventional computing based on physical devices. While such computing devices mimic brain-inspired analog information processing, the learning process still relies on methods optimized for numerical processing, such as backpropagation, which are not suitable for physical implementation.

Here, a research team from Japan's NTT Device Technology Labs (NTT Device Technology Labs) and the University of Tokyoby extending a method called direct feedback alignment (DFA) Biologically inspired training algorithms to demonstrate physical deep learning.Unlike the original algorithm, the proposed method is based on random projections with alternative nonlinear activations. Therefore, physical neural networks can be trained without knowledge of the physical system and its gradients. Furthermore, the computation of this training can be simulated on scalable physical hardware.

The researchers demonstrated a proof-of-concept using an optoelectronic recurrent neural network called a deep reservoir computer. The potential for accelerated computing with competitive performance on benchmarks is demonstrated. The results provide practical solutions for training and acceleration of neuromorphic computing.

The research is titled "Physical deep learning with biologically inspired training method: gradient-free approach for physical hardware" and was released on December 26, 2022 In "Nature Communications".

Physical Deep Learning

The record-breaking performance of artificial neural network (ANN)-based machine learning in image processing, speech recognition, gaming, and more has successfully demonstrated its excellence Ability. Although these algorithms resemble the way the human brain works, they are essentially implemented at the software level using traditional von Neumann computing hardware. However, such digital computing-based artificial neural networks face problems in energy consumption and processing speed. These issues motivate the use of alternative physical platforms for the implementation of artificial neural networks.

Interestingly, even passive physical dynamics can be used as computational resources in randomly connected ANNs. Known as a Physical Reservoir Computer (RC) or Extreme Learning Machine (ELM), the ease of implementation of this framework greatly expands the choice of achievable materials and their range of applications. Such physically implemented neural networks (PNNs) are able to outsource task-specific computational load to physical systems.

Building deeper physical networks is a promising direction to further improve performance, as they can exponentially expand network expressive capabilities. This motivates proposals for deep PNNs using various physical platforms. Their training essentially relies on a method called backpropagation (BP), which has achieved great success in software-based ANNs. However, BP is not suitable for PNN in the following aspects. First, the physical implementation of BP operations remains complex and not scalable. Second, BP requires an accurate understanding of the entire physical system. Furthermore, when we apply BP to RC, these requirements undermine the unique properties of physical RC, namely that we need to accurately understand and simulate black-box physical stochastic networks.

Like BP in PNN, the difficulty of operating BP in biological neural networks has also been pointed out by the brain science community; the rationality of BP in the brain has always been questioned. These considerations have led to the development of biologically sound training algorithms.

A promising recent direction is direct feedback alignment (DFA). In this algorithm, a fixed random linear transformation of the final output layer error signal is used to replace the reverse error signal. Therefore, this method does not require layer-by-layer propagation of error signals or knowledge of weights. Furthermore, DFA is reported to be scalable to modern large network models. The success of this biologically motivated training suggests that there is a more suitable way to train PNN than BP. However, DFA still requires the derivative f'(a) of the nonlinear function f(x) for training, which hinders the application of the DFA method in physical systems. Therefore, larger scaling of DFA is important for PNN applications.

DFA and its enhancement for deep learning in physics

Here, researchers demonstrate deep learning in physics by enhancing the DFA algorithm. In the enhanced DFA, we replace the derivative of the physical nonlinear activation f'(a) in the standard DFA with an arbitrary nonlinear g(a) and show that the performance is robust to the choice of g(a). Due to this enhancement, it is no longer necessary to model f'(a) accurately. Since the proposed method is based on parallel stochastic projections with arbitrary nonlinear activations, the training computations can be performed on physical systems in the same way as physical ELM or RC concepts. This enables physical acceleration of inference and training.

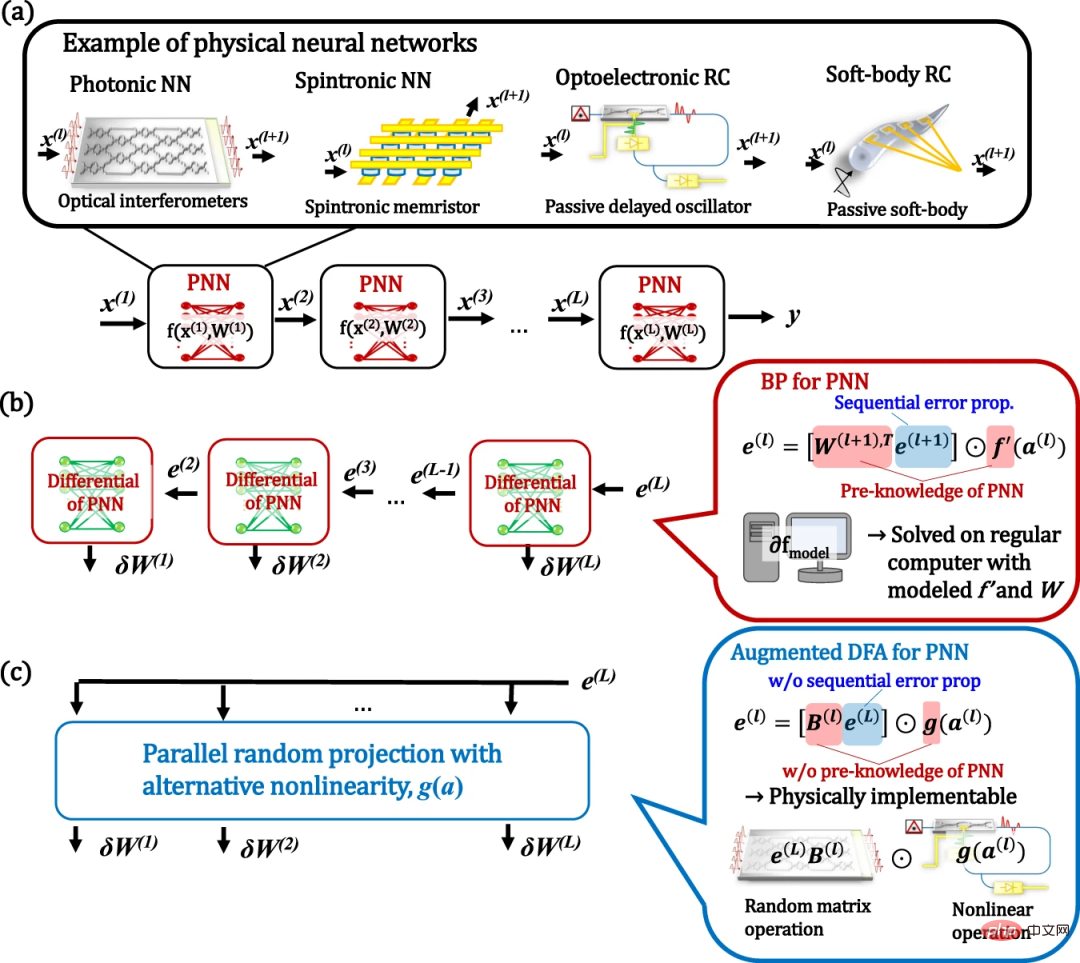
#Figure: Concept of PNN and its training through BP and augmented DFA. (Source: Paper)

#To demonstrate proof-of-concept, the researchers built an FPGA-assisted optoelectronic deep physics RC as a workbench. Although benchtop is simple to use and can be applied to a variety of physical platforms with only software-level updates, it achieves performance comparable to large and complex state-of-the-art systems.

Figure: Optoelectronic depth RC system with enhanced DFA training. (Source: paper)

# In addition, the entire processing time, including the time of digital processing, was compared, and the possibility of physical acceleration of the training process was found.

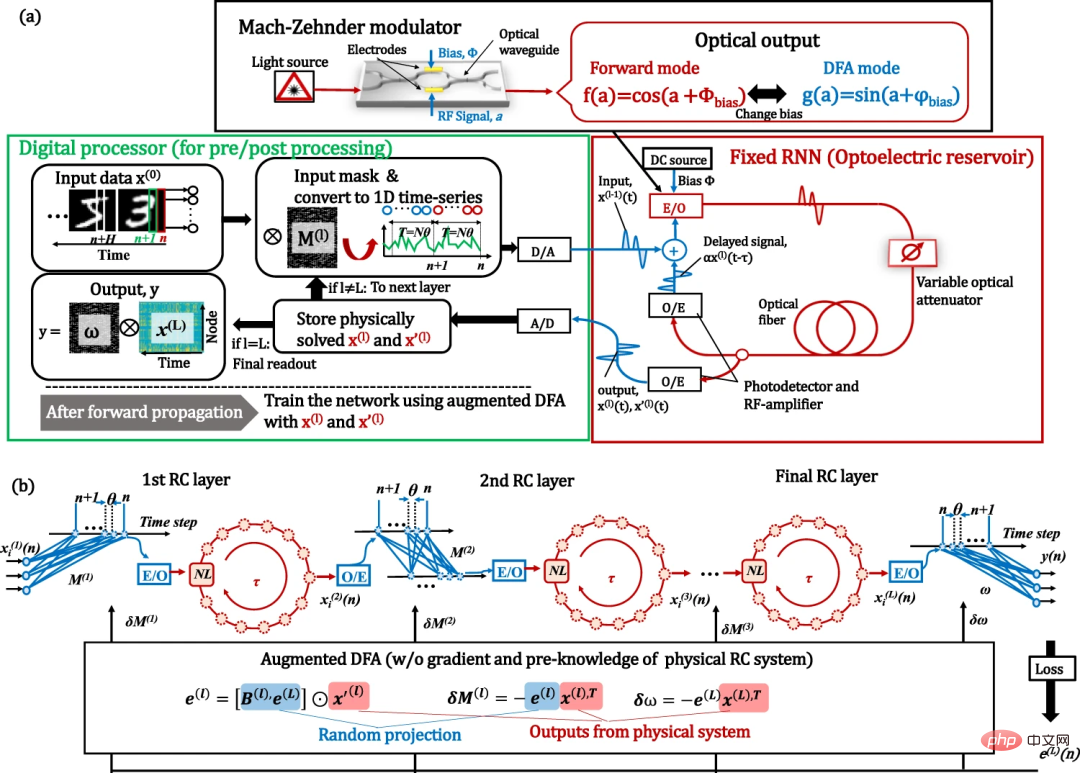
Figure: Performance of optoelectronic deep RC system. (Source: Paper)

The processing time budget for the RC bench breaks down as follows: FPGA processing (data transfer, memory allocation, and DAC/ADC) ~92%; 8% of digital processing is used for pre-/post-processing. Therefore, at the current stage, processing time is dominated by numerical calculations on FPGAs and CPUs. This is because the optoelectronic bench implements one reservoir using only one nonlinear delay line; these limitations could be relaxed by using fully parallel and all-optical computing hardware in the future. As can be seen, the computation on CPU and GPU shows a trend of O(N^2) for the number of nodes, while benchtop shows O(N), which is due to the data transfer bottleneck.

Physical acceleration outside the CPU is observed at N ~5,000 and ~12,000 for the BP and enhanced DFA algorithms, respectively. However, in terms of computational speed, effectiveness against GPUs has not been directly observed due to their memory limitations. By extrapolating the GPU trend, a physics speedup over the GPU can be observed at N ~80,000. To our knowledge, this is the first comparison of the entire training process and the first demonstration of physical training acceleration using PNNs.

To study the applicability of the proposed method to other systems, numerical simulations were performed using the widely studied photonic neural network. Furthermore, experimentally demonstrated delay-based RC is shown to be well suited for various physical systems. Regarding the scalability of physical systems, the main issue in building deep networks is their inherent noise. The effects of noise are studied through numerical simulations. The system was found to be robust to noise.

Scalability and limitations of the proposed approach

Here, the scalability of the DFA-based approach to more modern models is considered. One of the most commonly used models for practical deep learning is the deep connected convolutional neural network (CNN). However, it has been reported that the DFA algorithm is difficult to apply to standard CNNs. Therefore, the proposed method may be difficult to apply to convolutional PNNs in a simple manner.

Suitability for SNN is also an important topic considering the simulation hardware implementation. The applicability of DFA-based training to SNN has been reported, which means that the enhanced DFA proposed in this study can make training easier.

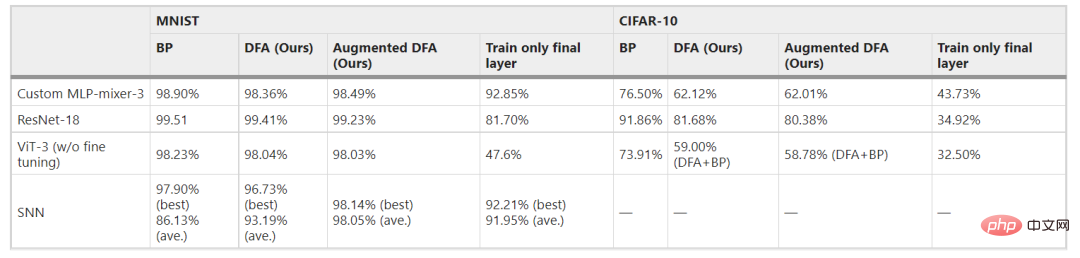
While DFA-based algorithms have the potential to be extended to more practical models than simple MLP or RC, the effectiveness of applying DFA-based training to such networks remains unknown. Here, as an additional work to this study, the scalability of DFA-based training (DFA itself and enhanced DFA) to the above mentioned models (MLP-Mixer, Vision transformer (ViT), ResNet and SNN) is investigated. DFA-based training was found to be effective even for exploratory practical models. Although the achievable accuracy of DFA-based training is essentially lower than that of BP training, some adjustments to the model and/or algorithm can improve performance. Notably, the accuracy of DFA and enhanced DFA was comparable for all experimental settings explored, suggesting that further improvements in DFA itself will directly contribute to improving enhanced DFA. The results show that the method can be extended to future implementations of practical models of PNNs, not just simple MLP or RC models.

Table 1: Applicability of enhanced DFA to real network models. (Source: paper)

BP and DFA in physical hardware

Generally Say, BP is very difficult to implement on physical hardware because it requires all the information in the computational graph. Therefore, training on physical hardware has always been done through computational simulations, which incurs large computational costs. Furthermore, differences between the model and the actual system lead to reduced accuracy. In contrast, enhanced DFA does not require accurate prior knowledge about the physical system. Therefore, in deep PNN, DFA-based methods are more effective than BP-based methods in terms of accuracy. Additionally, physical hardware can be used to accelerate computations.

In addition, DFA training does not require sequential error propagation calculated layer by layer, which means that the training of each layer can be performed in parallel. Therefore, a more optimized and parallel DFA implementation may lead to more significant speedups. These unique characteristics demonstrate the effectiveness of DFA-based methods, especially for neural networks based on physical hardware. On the other hand, the accuracy of the enhanced DFA-trained model is still inferior to that of the BP-trained model. Further improving the accuracy of DFA-based training remains future work.

Further physics speedup

The physics implementation demonstrates the speedup of RC loop processing with large-node numbers. However, its advantages are still limited and further improvements are needed. The processing time of the current prototype is expressed as data transfer and memory allocation to the FPGA. Therefore, integrating all processes into an FPGA will greatly improve performance at the expense of experimental flexibility. Furthermore, in the future, airborne optical methods will significantly reduce transmission costs. Large-scale optical integration and on-chip integration will further improve the performance of optical computing itself.

The above is the detailed content of Physical Deep Learning with Biologically Inspired Training Methods: A Gradient-Free Approach to Physical Hardware. For more information, please follow other related articles on the PHP Chinese website!