

It has to be said that scientists have been obsessed with giving AI math lessons recently.
No, the Facebook team also joined in the fun and proposed a new model that can completely automate the demonstration of theorems and is significantly better than SOTA.
You must know that as mathematical theorems become more complex, it will only become more difficult to prove the theorems solely by human power.
Therefore, using computers to demonstrate mathematical theorems has become a research focus.
OpenAI has previously proposed a model GPT-f that specializes in this direction, which can demonstrate 56% of the problems in Metamath.
The latest method proposed this time can increase this number to 82.6%.
At the same time, researchers say that this method takes less time and can reduce computing consumption to one-tenth of the original compared to GPT-f.
Could it be said that this time AI will succeed in its battle with mathematics?
The method proposed in this article is an online training program based on Transformer.
can be roughly divided into three steps:
First, pre-training in the mathematical proof library;
Second , Fine-tune the policy model on the supervised data set;
Third, Online training of the policy model and judgment model.
Specifically, it uses a search algorithm to let the model learn from the existing mathematical proof library, and then promotes and proves more problems.
The mathematical proof library includes three types, namely Metamath, Lean and a self-developed proof environment.
To put it simply, these proof libraries convert ordinary mathematical language into a form similar to a programming language.
Metamath’s main library is set.mm, which contains about 38,000 proofs based on ZFC set theory.
Lean is better known as Microsoft’s AI algorithm that can participate in IMO competitions. The Lean library is designed to teach the algorithm of the same name all the undergraduate mathematics knowledge and let it learn to prove these theorems.
The main goal of this research is to build a prover that can automatically generate a series of suitable strategies to prove the problem.
To this end, the researchers proposed a non-equilibrium hypergraph proof search algorithm based on MCTS.
MCTS is translated as Monte Carlo Tree Search, which is often used to solve game tree problems. It is well-known because of AlphaGo.
Its operation process is to find promising actions by randomly sampling in the search space, and then expand the search tree based on this action.
The idea adopted in this study is similar to this.
The search proof process starts from goal g, searches downward for methods, and gradually develops into a hypergraph.
When an empty set appears under a branch, it means that an optimal proof has been found.
Finally, during the backpropagation process, record the node values and total number of operations of the supertree.
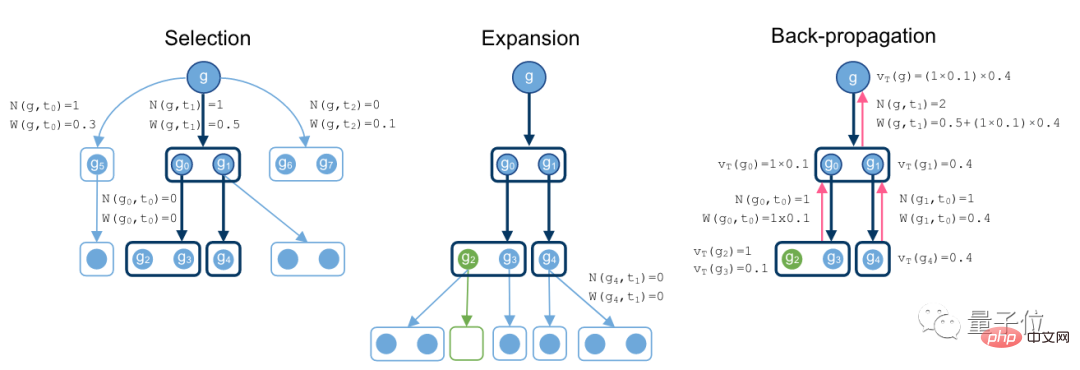
In this link, the researchers assumed a strategy model and a judgment model.
The strategy model allows sampling by judgment models, which can evaluate the current strategy's ability to find proof methods.
The entire search algorithm uses the above two models as a reference.
These two models are Transformer models and share weights.
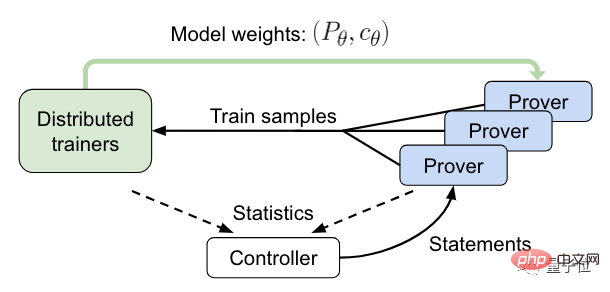
Next, comes the online training stage.
In this process, the controller will send the statement to asynchronous HTPS verification and collect training and proof data.
The validator will then send the training samples to the distributed trainer and periodically synchronize its model copies.
In the testing session, the researchers compared HTPS with GPT-f.
The latter is a mathematical theorem reasoning model previously proposed by OpenAI, also based on Transformer.
The results show that the model after online training can prove 82% of the problems in Metamath, far exceeding the previous record of 56.5% of GPT-f.

In the Lean library, this model can prove 43% of the theorems, which is 38% higher than SOTA. The following are the IMO test questions proved by this model.

#But it’s not perfect yet.
For example, in the following question, it did not solve the question in the simplest way. The researchers said this was because of errors in the annotations.

Using computers to demonstrate mathematical problems, the proof of the four-color theorem is one of the most well-known examples.
The four-color theorem is one of the three major problems in modern mathematics. It states that "any map can use only four colors to color countries with common borders in different colors."
Because the demonstration of this theorem requires a lot of calculations, no one could fully demonstrate it within 100 years after it was proposed.
Until 1976, after 1,200 hours and 10 billion judgments on two computers at the University of Illinois, it was finally possible to demonstrate that any map only needs 4 colors to mark it. It caused a sensation in the entire mathematical community.
In addition, as mathematical problems become more complex, it becomes more difficult to use human power to check whether the theorem is correct.
Recently, the AI community has gradually focused on mathematical problems.
In 2020, OpenAI launched the mathematical theorem reasoning model GPT-f, which can be used for automatic theorem proof.
This method can complete 56.5% of the proofs in the test set, exceeding the then SOTA model MetaGen-IL by more than 30%.
In the same year, Microsoft also released Lean, which can make IMO test questions, which means that AI can make questions that it has never seen before.
Last year, after OpenAI added a verifier to GPT-3, the effect of doing math problems was significantly better than the previous fine-tuning method, and it could reach 90% of the level of primary school students.
In January this year, a joint study from MIT, Harvard, Columbia University, and the University of Waterloo showed that the model they proposed can do high math.
In short, scientists are working hard to make AI, a partial subject, become both liberal arts and sciences.
The above is the detailed content of AI can prove 82% of the problems in mathematical databases. The new SOTA has been achieved, and it is still based on Transformer.. For more information, please follow other related articles on the PHP Chinese website!




