
Sympy
Sympy is a mathematical symbol library (sym stands for symbol, symbol), including various mathematical operation methods such as integrals and differential equations, and is provided for python Provides powerful mathematical operation support. For images, although they are all doing discrete calculations, and the most operations are arrays in numpy, but in fact, this library contains the most basic mathematical operations such as integral differential, trigonometry, etc. It can be said to be the most basic in engineering. Use It's comparable to matlab.

sympy installation
sudo pip install sympy or sudo pip3 install sympy
If you use anaconda then conda install sympy
Related recommendations:《python视频》
odeint() function
odeint() function is a scipy library A function that numerically solves differential equations
odeint() function requires at least three variables. The first is the differential equation function, the second is the initial value of the differential equation, and the third is the independent variable of the differential.
Example:
#y"+a*y'+b*y=0
from scipy.integrate import odeint #使用odeint之前,首先从scipy.integrate中调用它from pylab import *
def deriv(y,t): # 返回值是y和y的导数组成的数组
a = -2.0
b = -0.1
return array([ y[1], a*y[0]+b*y[1] ])
time = linspace(0.0,50.0,1000)
yinit = array([0.0005,0.2]) # 初值
y = odeint(deriv,yinit,time)
figure()
plot(time,y[:,0],label='y') #y[:,0]即返回值的第一列,是y的值。label是为了显示legend用的。
plot(time,y[:,1],label="y'") #y[:,1]即返回值的第二列,是y’的值
xlabel('t')
ylabel('y')
legend()
show()The output results are as follows:
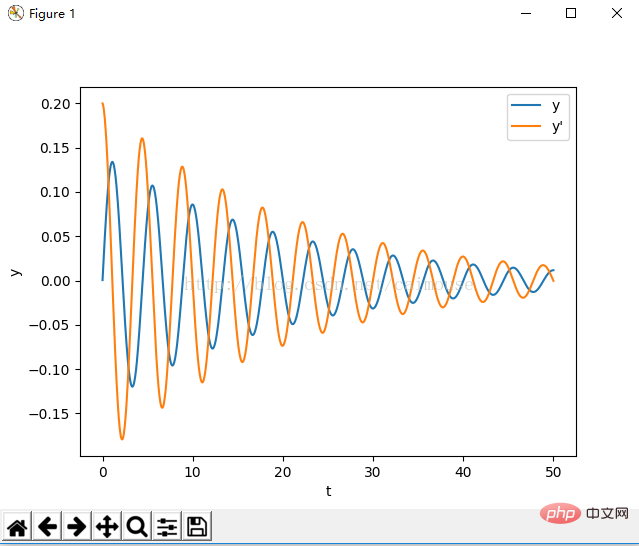
The above is the detailed content of Can python solve differential equations?. For more information, please follow other related articles on the PHP Chinese website!