Python implements the method of solving the greatest common divisor-Python Tutorial-php.cn

This time I will bring youPythonHow to solve the greatest common divisor. What are theprecautionsfor Python to solve the greatest common divisor. The following is a practical case. Let’s take a look. one time.

Firstly, I excerpt a description of the algorithm from the Internet as follows:

Change phase subtraction method: also called update phase subtraction method, it is a maximum convention from "Nine Chapters of Arithmetic" It is an algorithm for numbers. It was originally designed for reduction, but it is suitable for any situation where the greatest common divisor needs to be found.

"Nine Chapters on Arithmetic" is an ancient Chinese mathematics treatise. The "Additional Subtraction Technique" in it can be used to find the greatest common divisor of two numbers, that is, "the one that can be half." Half, if half is not allowed, substitute the number of the denominator and son, and subtract the greater from the less, and find the equal number. "

##Translated into modern language as follows. :

Step one: Given any two positive

integers; determine whether they are both even numbers. If yes, use 2 to reduce; if not, perform the second step.

Step 2: Subtract the smaller number from the larger number, then compare the resulting difference with the smaller number, and reduce the number from the larger number. Continue this operation until the resulting subtrahend and difference are equal.

After reading the above description, my first reaction was, is there something wrong with this description? In terms of universality, there should be problems. For example, if I find the greatest common divisor of 4 and 4, but after half and half, the result must be wrong! The following algorithm cannot be performed either!

Anyway, let’s implement the above algorithm description first:

# -*- coding:utf-8 -*- #! python2 def MaxCommpisor(m,n): # even process while m % 2 == 0 and n % 2 == 0: m = m / 2 n = n / 2 # exchange order when needed if m < n: m,n = n,m # calculate the max comm pisor while m - n != n: diff = m - n if diff > n: m = diff else: m = n n = diff return n print(MaxCommpisor(55,120)) print(MaxCommpisor(55,77)) print(MaxCommpisor(32,64)) print(MaxCommpisor(16,128))

Copy after login

Running results:

Needless to say, the above program execution error All kinds of things. So how to correct it?

First of all, everything divided by 2 should be counted back in the end! In this way, the program is modified as follows:

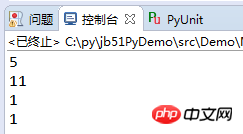
def MaxCommpisor(m,n): com_factor = 1 if m == n: return n else: # process for even number while m % 2 == 0 and n % 2 == 0: m = int(m / 2) n = int(n / 2) com_factor *= 2 if m < n: m,n = n,m diff = m - n while n != diff: m = diff if m < n: m,n = n,m diff = m - n return n * com_factor print(MaxCommpisor(55,120)) print(MaxCommpisor(55,77)) print(MaxCommpisor(32,64)) print(MaxCommpisor(16,128))

Copy after login

After modification, the execution result of the above program is as follows

Although this program looks a bit strange when written, but The overall algorithm is still implemented. Compared with algorithms such as euclidean division, this probability will be reduced to a certain extent at the

looplevel. Especially for the last two pairs of test numbers, the effect is better in this case. However, I am not yet able to give an accurate measurement of the overall efficiency of the algorithm.

I believe you have mastered the method after reading the case in this article. For more exciting information, please pay attention to other related articles on the php Chinese website!