Beyond JavaScript - Why + doesn&#t equal in programming

當開發者第一次遇到這個看似令人費解的結果時，JavaScript 經常受到嘲笑：

0.1 + 0.2 == 0.30000000000000004

關於 JavaScript 處理數字的迷因很普遍，常常導致許多人相信這種行為是該語言所獨有的。

然而，這個怪癖不僅限於 JavaScript。這是大多數程式語言處理浮點運算方式的結果。

例如，以下是來自 Java 和 Go 的程式碼片段，它們產生類似的結果：

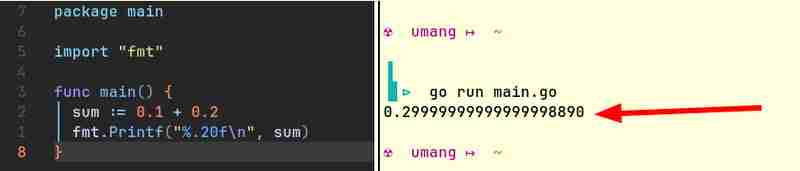
電腦本身只能儲存整數。他們不懂分數。 （他們會怎麼做？電腦進行算術運算的唯一方法是打開或關閉一些燈。燈可以打開或關閉。它不能「半」亮！）他們需要某種表示浮點數的方法。由於這種表示方法並不完全準確，因此 0.1 + 0.2 通常不等於 0.3。

所有分母由數係基數的質因數組成的分數都可以清晰地表達，而任何其他分數都會有重複的小數。例如，在以10 為基數的數字系統中，可以清楚地表示1/2、1/4、1/5、1/10 等分數，因為每種情況下的分母均由2 或5（10 的質因數）組成. 然而，像1/3、1/6、1/7 這樣的分數都有循環小數。

同樣，在二進位系統中，像 1/2、1/4、1/8 這樣的分數都可以清晰地表達，而所有其他分數都有循環小數。當您對這些循環小數執行算術運算時，您最終會得到剩餘的內容，當您將計算機的數字二進製表示形式轉換為人類可讀的以 10 為基數的表示形式時，這些剩餘內容會繼續存在。這就是導致大致正確結果的原因。

既然我們已經確定這個問題並非 JavaScript 所獨有，那麼讓我們探討一下浮點數是如何在幕後表示和處理的，以了解為什麼會出現這種行為。

為了了解浮點數在底層是如何表示和處理的，我們首先必須了解 IEEE 754 浮點標準。

IEEE 754 標準是一種廣泛使用的規範，用於在電腦系統中表示浮點數並對其執行算術運算。它的創建是為了確保在各種計算平台上使用浮點運算時的一致性。大多數程式語言和硬體實作（CPU、GPU 等）都遵守此標準。

這是用 IEEE 754 格式表示數字的方式：

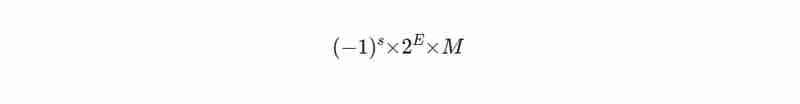
這裡s是符號位（0代表正，1代表負），M是尾數（保存數字的數字）和E 是決定數字大小的指數。

您將無法找到任何可以以這種格式精確表示數字（如 0.1、0.2 或 0.3）的 M 和 E 整數值。我們只能選擇給出最接近結果的 M 和 E 值。

這是一個可用來決定十進位數的 IEEE 754 表示法的工具：https://www.h-schmidt.net/FloatConverter/IEEE754.html

IEEE 754 0.25 表示法：

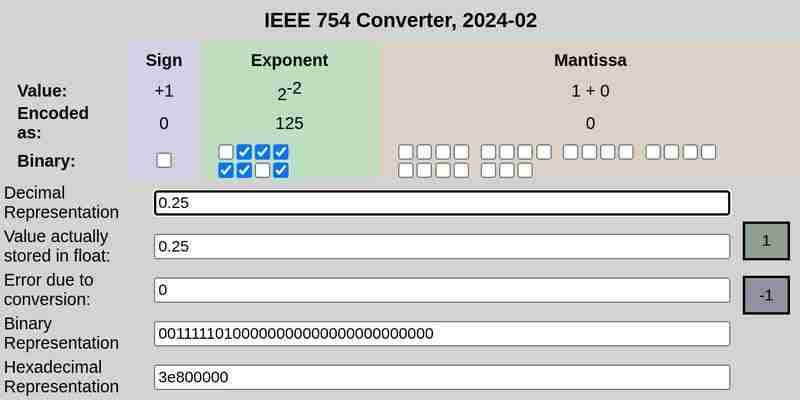
IEEE 754 分別表示 0.1 與 0.2：

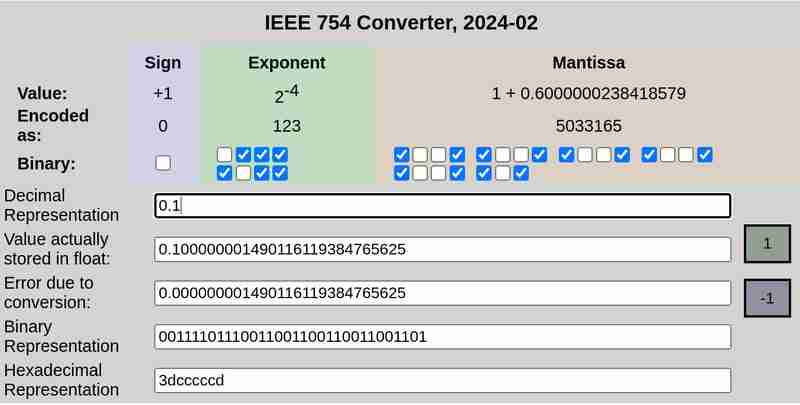
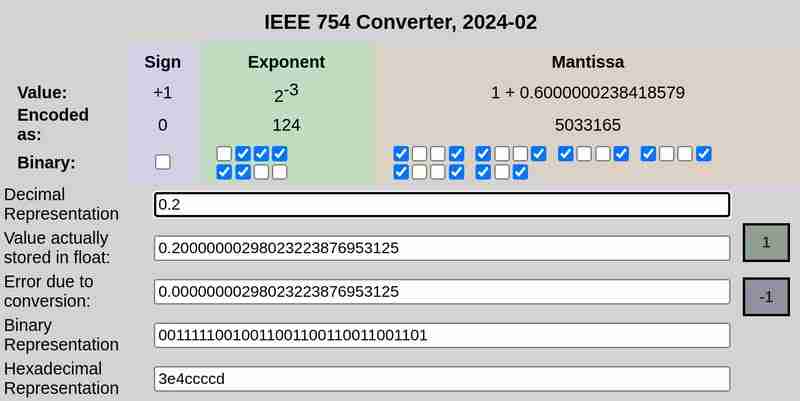
請注意，0.25 時轉換誤差為 0，而 0.1 和 0.2 則為非零誤差。

IEEE 754 定義了以下表示浮點數的格式：

• 單精確度（32 位元）：1 位元符號，8 位元指數，23 位元尾數

• 雙精確度（64 位元）：1 位元符號，11 位元指數，52 位元尾數

為了簡單起見，讓我們考慮使用 32 位元的單精度格式。

0.1 的 32 位元表示為：

0 01111011 10011001100110011001101

Here the first bit represents the sign (0 which means positive in this case), the next 8 bits (01111011) represent the exponent and the final 23 bits (10011001100110011001101) represent the mantissa.

This is not an exact representation. It represents ≈ 0.100000001490116119384765625

Similarly, the 32 bit representation of 0.2 is:

0 01111100 10011001100110011001101

This is not an exact representation either. It represents ≈ 0.20000000298023223876953125

When added, this results in:

0 01111101 11001101010011001100110 

which is ≈ 0.30000001192092896 in decimal representation.

In conclusion, the seemingly perplexing result of 0.1 + 0.2 not yielding 0.3 is not an anomaly specific to JavaScript, but a consequence of the limitations of floating-point arithmetic across programming languages. The roots of this behaviour lie in the binary representation of numbers, which inherently leads to precision errors when handling certain fractions.

The above is the detailed content of Beyond JavaScript - Why + doesn&#t equal in programming. For more information, please follow other related articles on the PHP Chinese website!