Minimum Cost to Connect Two Groups of Points

1595. Minimum Cost to Connect Two Groups of Points

Difficulty:Hard

Topics:Array, Dynamic Programming, Bit Manipulation, Matrix, Bitmask

You are given two groups of points where the first group has size₁points, the second group has size₂points, and size₁>= size₂.

The cost of the connection between any two points are given in an size₁x size₂matrix where cost[i][j] is the cost of connecting point i of the first group and point j of the second group. The groups are connected ifeach point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.

Returnthe minimum cost it takes to connect the two groups.

Example 1:

• Input:cost = [[15, 96], [36, 2]]
• Output:17
• Explanation:The optimal way of connecting the groups is:

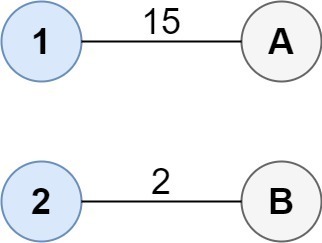
1--A 2--B This results in a total cost of 17.

Example 2:

• Input:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
• Output:4
• Explanation:The optimal way of connecting the groups is:

1--A 2--B 2--C 3--A This results in a total cost of 4.

Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.

Example 3:

• Input:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
• Output:10

Constraints:

• size₁== cost.length
• size₂== cost[i].length
• 1 <= size₁, size₂<= 12
• size₁>= size₂
• 0 <= cost[i][j] <= 100

Hint:

1. Each point on the left would either be connected to exactly point already connected to some left node, or a subset of the nodes on the right which are not connected to any node
2. Use dynamic programming with bitmasking, where the state will be (number of points assigned in first group, bitmask of points assigned in second group).

Solution:

We can leverage dynamic programming with bitmasking. The idea is to minimize the cost by considering each point in the first group and trying to connect it to all points in the second group.

Dynamic Programming (DP) Approach with Bitmasking

Steps:

1. State Representation:

   • Use a DP table dp[i][mask] where:
     • i is the index in the first group (ranging from 0 to size1-1).
     • mask is a bitmask representing which points in the second group have been connected.

2. State Transition:

   • For each point in the first group, try connecting it to every point in the second group, updating the DP table accordingly.
   • If a new point in the second group is connected, update the corresponding bit in the mask.

3. Base Case:

   • Start with dp[0][0] = 0 (no connections initially).

4. Goal:

   • Compute the minimum cost for dp[size1][(1 << size2) - 1], which represents connecting all points from both groups.

Let's implement this solution in PHP:1595. Minimum Cost to Connect Two Groups of Points

        
Explanation:
        

         
The DP array dp[i][mask] stores the minimum cost to connect the first i points from group 1 with the points in group 2 as indicated by mask.
         
The nested loops iterate over each combination of i and mask, trying to find the optimal cost by considering all possible connections.
         
In the end, the solution calculates the minimum cost considering the scenarios where some points in the second group may still be unconnected, ensuring all points are connected.
        
This approach efficiently handles the problem's constraints and ensures the minimum cost for connecting the two groups.
Contact Links
이 시리즈가 도움이 되었다면 GitHub에서저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!
이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.
        

         
링크드인
         
깃허브
        
The above is the detailed content of Minimum Cost to Connect Two Groups of Points. For more information, please follow other related articles on the PHP Chinese website!