Modify Graph Edge Weights

2699. Modify Graph Edge Weights

Difficulty:Hard

Topics:Graph, Heap (Priority Queue), Shortest Path

You are given anundirected weighted connectedgraph containing n nodes labeled from 0 to n - 1, and an integer array edges where edges[i] = [a_i, b_i, w_i] indicates that there is an edge between nodes a_iand b_iwith weight w_i.

Some edges have a weight of -1 (w_i= -1), while others have apositiveweight (w_i> 0).

Your task is to modifyall edgeswith a weight of -1 by assigning thempositive integer valuesin the range [1, 2 * 10⁹] so that theshortest distancebetween the nodes source and destination becomes equal to an integer target. If there aremultiple modificationsthat make the shortest distance between source and destination equal to target, any of them will be considered correct.

Returnan array containing all edges (even unmodified ones) in any order if it is possible to make the shortest distance from source to destination equal to target, or anempty arrayif it's impossible.

Note:You are not allowed to modify the weights of edges with initial positive weights.

Example 1:

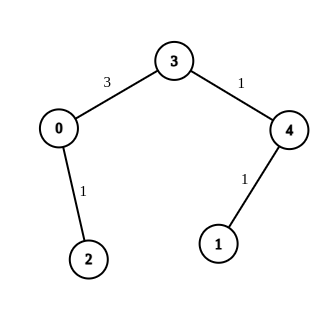
• Input:n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
• Output:[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
• Explanation:The graph above shows a possible modification to the edges, making the distance from 0 to 1 equal to 5.

Example 2:

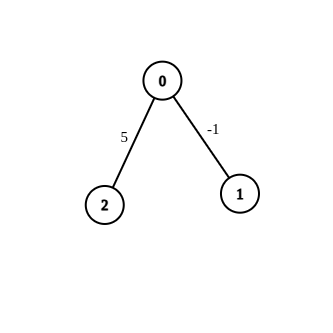
• Input:n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
• Output:[]
• Explanation:The graph above contains the initial edges. It is not possible to make the distance from 0 to 2 equal to 6 by modifying the edge with weight -1. So, an empty array is returned.

Example 3:

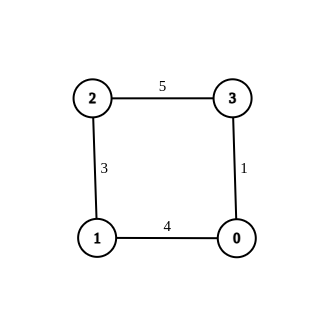
• Input:n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
• Output:[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
• Explanation:The graph above shows a modified graph having the shortest distance from 0 to 2 as 6.

Constraints:

• 1 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= a_i, b_i< n
• w_i= -1 or 1 <= w_i<= 10⁷
• a_i!= b_i
• 0 <= source, destination < n
• source != destination
• 1 <= target <= 10⁹
• The graph is connected, and there are no self-loops or repeated edges

Hint:

1. Firstly, check that it’s actually possible to make the shortest path from source to destination equal to the target.
2. If the shortest path from source to destination without the edges to be modified, is less than the target, then it is not possible.
3. If the shortest path from source to destination including the edges to be modified and assigning them a temporary weight of 1, is greater than the target, then it is also not possible.
4. Suppose we can find a modifiable edge (u, v) such that the length of the shortest path from source to u (dis1) plus the length of the shortest path from v to destination (dis2) is less than target (dis1 + dis2 < target), then we can change its weight to “target - dis1 - dis2”.
5. For all the other edges that still have the weight “-1”, change the weights into sufficient large number (target, target + 1 or 200000000 etc.).

Solution:

We can break down the approach as follows:

Approach:

1. Initial Check with Existing Weights:

   • 먼저, 가중치가 -1인 가장자리는 무시하고 양의 가중치를 갖는 가장자리만 사용하여 소스에서 대상까지의 최단 경로를 계산합니다.
   • 이 거리가 이미 목표보다 크다면 목표를 달성하기 위해 -1 가장자리를 수정할 수 없으므로 빈 배열을 반환합니다.

2. 임시 가중치 부여 1:

   • 다음으로 가중치가 -1인 모든 가장자리에 임시 가중치 1을 할당하고 최단 경로를 다시 계산합니다.
   • 이 최단 경로가 여전히 목표보다 크면 목표를 달성하는 것이 불가능하므로 빈 배열을 반환합니다.

3. 특정 가장자리 가중치 수정:

   • 가중치 -1로 가장자리를 반복하고 목표 거리와 정확히 일치하도록 조정될 수 있는 가장자리를 식별합니다. 이는 이 가장자리로 향하는 경로와 가장자리에서 나오는 경로의 결합된 거리가 정확한 목표 거리가 되도록 가장자리의 가중치를 조정하여 수행됩니다.
   • 나머지 -1 에지에는 최단 경로에 영향을 주지 않도록 충분히 큰 가중치(예: 2 * 10^9)를 할당하세요.

4. 수정된 가장자리 반환:

   • 마지막으로 수정된 가장자리 목록을 반환합니다.

PHP에서 이 솔루션을 구현해 보겠습니다:2699. 그래프 가장자리 가중치 수정

설명:

• dijkstra 함수는 소스에서 다른 모든 노드까지의 최단 경로를 계산합니다.
• 처음에는 -1 모서리를 무시하고 최단 경로를 계산합니다.
• -1 모서리가 없는 경로가 목표보다 작으면 함수는 빈 배열을 반환하여 목표를 충족하도록 가중치를 조정할 수 없음을 나타냅니다.
• 그렇지 않으면 일시적으로 모든 -1 가장자리를 1로 설정하고 최단 경로가 목표를 초과하는지 확인합니다.
• 그렇다면 다시 목표에 도달하는 것이 불가능하며 빈 배열을 반환합니다.
• 그런 다음 -1 모서리의 가중치를 전략적으로 수정하여 정확한 목표의 원하는 최단 경로를 달성합니다.

이 접근 방식은 가장자리 가중치를 효율적으로 확인하고 조정하여 가능한 경우 목표 거리가 충족되도록 합니다.

연락처 링크

이 시리즈가 도움이 되었다면 GitHub에서저장소에 별표를 표시하거나 즐겨찾는 소셜 네트워크에서 게시물을 공유해 보세요. 여러분의 지원은 저에게 큰 의미가 될 것입니다!

이렇게 더 유용한 콘텐츠를 원하시면 저를 팔로우해주세요.

• 링크드인
• 깃허브

The above is the detailed content of Modify Graph Edge Weights. For more information, please follow other related articles on the PHP Chinese website!