Maximum Number of Points with Cost

1937. Maximum Number of Points with Cost

Difficulty:Medium

Topics:Array, Dynamic Programming

You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want tomaximizethe number of points you can get from the matrix.

To gain points, you must pick one cell ineach row. Picking the cell at coordinates (r, c) willaddpoints[r][c] to your score.

However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c₁) and (r + 1, c₂) willsubtractabs(c₁- c₂) from your score.

Returnthemaximumnumber of points you can achieve.

abs(x) is defined as:

• x for x >= 0.

• -x for x < 0.

Example 1:

• Input:l1 = [2,4,3], l2 = [5,6,4]
• Output:9
• Explanation:
  • The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0).
  • You add 3 + 5 + 3 = 11 to your score.
  • However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score.
  • Your final score is 11 - 2 = 9.

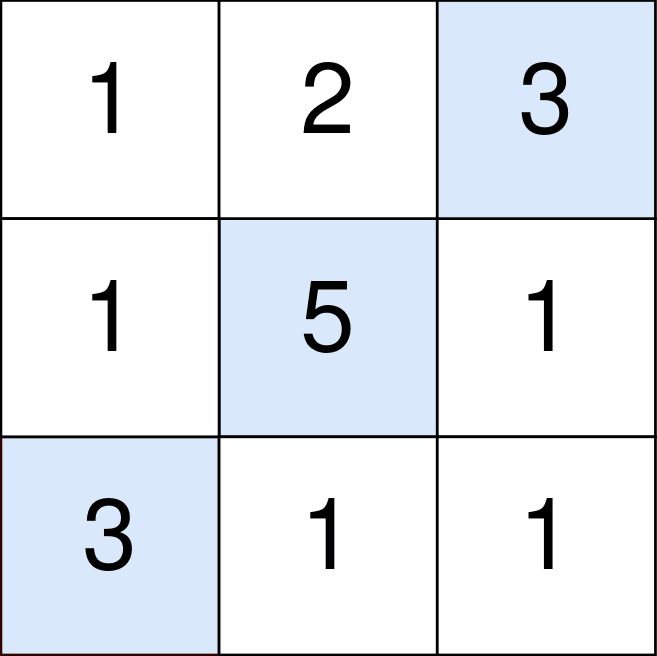
Example 2:

• Input:points = [[1,5],[2,3],[4,2]]
• Output:11
• Explanation:
  • The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0).
  • You add 5 + 3 + 4 = 12 to your score.
  • However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score.
  • Your final score is 12 - 1 = 11.

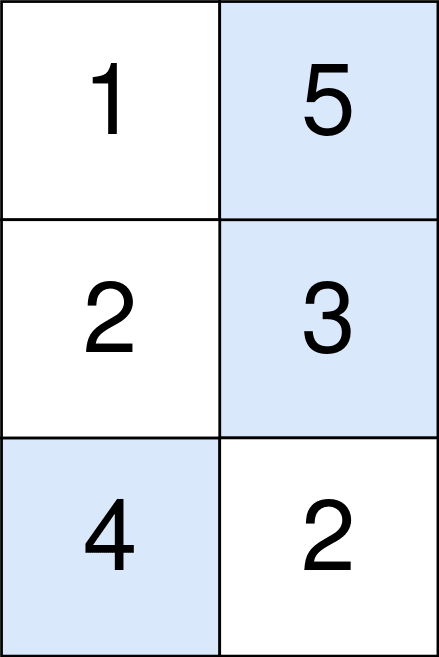
Constraints:

• m == points.length
• n == points[r].length
• 1 <= m, n <= 10⁵
• 1 <= m * n <= 10⁵
• 0 <= points[r][c] <= 10⁵

Hint:

1. Try using dynamic programming.
2. dp[i][j] is the maximum number of points you can have if points[i][j] is the most recent cell you picked.

Solution:

We can break down the solution into several steps:

Step 1: Define the DP Array

We will use a 2D array dp where dp[i][j] represents the maximum points we can achieve by selecting the cell at row i and column j.

Step 2: Initialize the DP Array

Initialize the first row of dp to be the same as the first row of points since there are no previous rows to subtract the cost.

Step 3: Calculate DP Values for Each Row

For each subsequent row, we calculate the maximum possible points for each column considering the costs of switching from the previous row.

To efficiently calculate the transition from row i-1 to row i, we can use two auxiliary arrays left and right:

• left[j] will store the maximum value we can achieve for the j-th column considering only transitions from the left.
• right[j] will store the maximum value we can achieve for the j-th column considering only transitions from the right.

Step 4: Update DP for Each Row

For each column j in row i:

• Update dp[i][j] using the maximum of either left[j] or right[j] plus points[i][j].

Step 5: Return the Maximum Value from the Last Row

The result will be the maximum value in the last row of the dp array.

Let's implement this solution in PHP:1937. Maximum Number of Points with Cost

        
Explanation:
        

         
left and right arrays:These help us compute the maximum points we can gain for each cell by considering the previous row's values, efficiently accounting for the penalty from moving across columns.
         
Dynamic programming approach:This method ensures that each row is calculated based on the previous row, making the solution scalable for large matrices.
        
This approach has a time complexity of (O(m times n)), which is efficient given the constraints.
Contact Links
このシリーズが役立つと思われた場合は、GitHub でリポジトリにスターを付けるか、お気に入りのソーシャル ネットワークで投稿を共有することを検討してください。あなたのサポートは私にとってとても意味のあるものになります！
このような役立つコンテンツがさらに必要な場合は、お気軽にフォローしてください:
        

         
リンクトイン
         
GitHub
        
The above is the detailed content of Maximum Number of Points with Cost. For more information, please follow other related articles on the PHP Chinese website!