
用光训练神经网络,清华成果最新登上了 Nature!
无法应用反向传播算法怎么办?
他们提出了一种全前向模式(Fully Forward Mode,FFM)的训练方法,在物理光学系统中直接执行训练过程,克服了传统基于数字计算机模拟的限制。

简单点说,以前需要对物理系统进行详细建模,然后在计算机上模拟这些模型来训练网络。而 FFM 方法省去了建模过程,允许系统直接使用实验数据进行学习和优化。
这也意味着,训练不需要再从后向前检查每一层(反向传播),而是可以直接从前向后更新网络的参数。
打个比方,就像拼图一样,反向传播需要先看到最终图片(输出),然后逆向一块块检查复原;而 FFM 方法更像手中已有部分完成的拼图,只需按照一些光原理(对称互易性)继续填充,而无需回头检查之前的拼图。

这样下来,使用 FFM优势也很明显:
一是减少了对数学模型的依赖,可以避免模型不准确带来的问题;二是节省了时间(同时能耗更低),使用光学系统可以并行处理大量的数据和操作,消除反向传播也减少了整个网络中需要检查和调整的步骤。
论文共同一作是来自清华的薛智威、周天贶,通讯作者是清华的方璐教授、戴琼海院士。此外,清华电子系徐智昊、之江实验室虞绍良也参与了这项研究。
消除反向传播
一句话概括 FFM 原理:
将光学系统映射为参数化的现场神经网络,通过测量输出光场来计算梯度,并使用梯度下降算法更新参数。
简单说就是让光学系统自学,通过观察自己如何处理光线(即测量输出光场)来了解自己的表现,然后利用这些信息来逐步调整自己的设置(参数)。
下图展示了 FFM 在光学系统中的运行机制:
其中 a 为传统设计方法的局限性;b 为光学系统的组成;c 为光学系统到神经网络的映射。

展开来说,一般的光学系统(b),包括自由空间透镜光学和集成光子学,由调制区域(暗绿色)和传播区域(浅绿色)组成。在这些区域中,调制区域的折射率是可调的,而传播区域的折射率是固定的。
而这里的调制和传播区域可以映射到神经网络中的权重和神经元连接。
在神经网络中,这些可调整的部分就像是神经元之间的连接点,可以改变它们的强度(权重)来学习。
利用空间对称互易性原理,数据和误差计算可以共享相同的前向物理传播过程和测量方法。
这有点像镜子里的反射,系统中的每个部分都能以相同的方式响应光的传播和错误反馈。这意味着无论光如何进入系统,系统都能以一致的方式处理它,并根据结果来调整自己。
这样,可以在现场直接计算梯度,用于更新设计区域内的折射率,从而优化系统性能。
通过现场梯度下降方法,光学系统可以逐步调整其参数,直至达到最优状态。
原文将上述全前向模式的梯度下降方法(替代反向传播)用方程最终表示为:
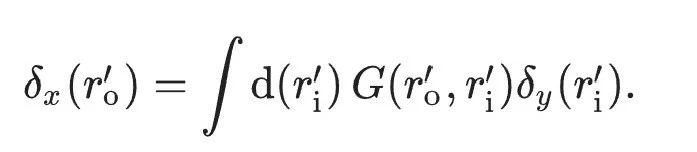
一种光学神经网络训练方法
作为一种光学神经网络训练的方法,FFM 有以下优势:
与理想模型相当的准确率
使用 FFM 可以在自由空间光学神经网络(Optical Neural Network,ONN)上实现有效的自训练过程。

要说明这个结论,研究人员首先用一个单层的ONN 在基准数据集上进行了对象分类训练(a)。
具体来说,他们用了一些手写数字的图片(MNIST 数据集)来训练这个系统,然后将结果进行了可视化(b)。
结果显示,通过 FFM 学习训练的 ONN 在实验光场与理论光场之间相似性极高(SSIM 超过 0.97)。
换句话说,它学习得非常好,几乎能够完美复制给它的示例。
However, researchers also remind:
Due to imperfections in the system, the theoretically calculated light fields and gradients cannot fully accurately reflect actual physical phenomena.
Next, the researchers used more complex images (Fashion-MNIST dataset) to train the system to recognize different fashion items.
In the beginning, when the number of layers increased from 2 to 8, the average accuracy of the computer-trained network was almost half of the theoretical accuracy.
With the FFM learning method, the network accuracy of the system has been increased to 92.5%, which is close to the theoretical value.
This shows that as the number of network layers increases, the performance of the network trained by traditional methods decreases, while FFM learning can maintain high accuracy.
At the same time, the performance of ONN can be further improved by incorporating nonlinear activation into FFM learning. In experiments, nonlinear FFM learning was able to improve classification accuracy from 90.4% to 93.0%.
Research further proves that by batch training non-linear ONN, the error propagation process can be simplified and the training time only increases by 1 to 1.7 times.
High-resolution focusing capability
FFM can also achieve high-quality imaging in practical applications, achieving resolution close to the physical limit even in complex scattering environments.
First of all, when light waves enter a scattering medium (such as fog, smoke or biological tissue, etc.), focusing will become complicated, but the propagation of light waves in the medium often maintains a certain symmetry.
FFM takes advantage of this symmetry by optimizing the propagation path and phase of light waves to reduce the negative impact of scattering effects on focusing.
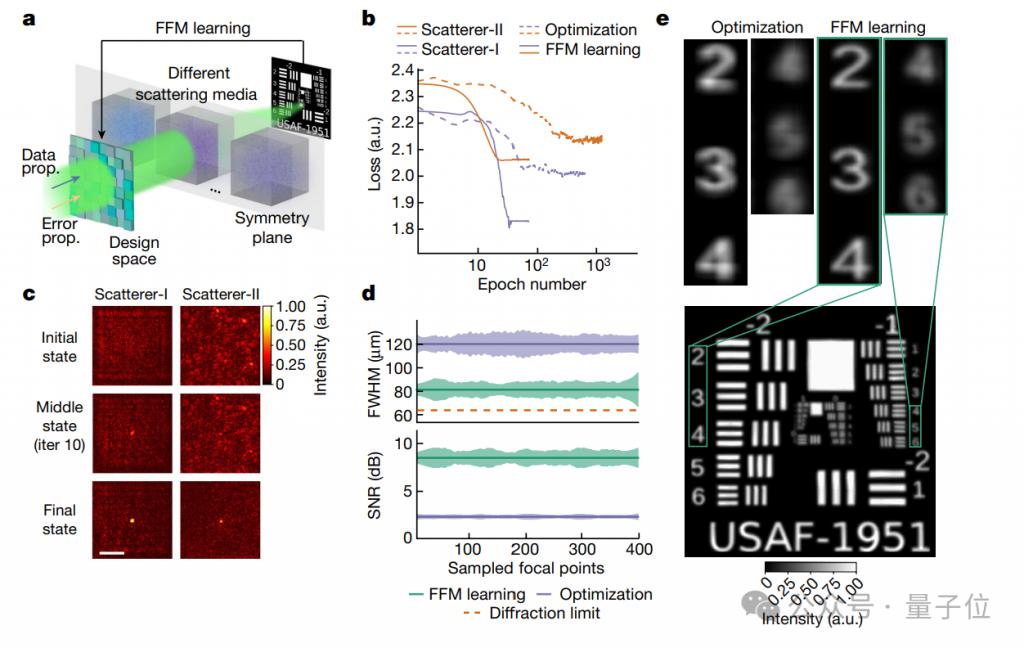
The effect is also very significant. Figure b shows the comparison of the two optimization methods, FFM and PSO (Particle Swarm Optimization).
Specifically, the experiment used two scattering media, one is a random phase plate (Scatterer-I) and the other is transparent tape (Scatterer-II).
In both media, FFM achieved convergence (finding the optimal solution faster) after only 25 design iterations, with convergence loss values of 1.84 and 2.07 respectively (lower is better performance).
The PSO method requires at least 400 design iterations to reach convergence, and the loss values at final convergence are 2.01 and 2.15.
At the same time, Figure c shows that FFM is able to continuously optimize itself, and the focus it is designed to gradually evolve and converge from an initial random distribution to a tight focus.
Within a design area of 3.2 mm × 3.2 mm, the researchers further uniformly sampled the FFM and PSO optimized foci and compared their FWHM (full width at half maximum) and PSNR (peak signal to noise ratio).
The results show that FFM has higher focusing accuracy and better imaging quality.
Figure e further evaluates the performance of the designed focus array when scanning a resolution map located behind a scattering medium.
The results are surprising. The focus size of the FFM design is close to the diffraction limit of 64.5 m, which is the theoretical highest resolution standard for optical imaging.
Able to parallelly image objects outside the line of sight
Since it is so powerful in scattering media, the researchers also tried non-line-of-sight (NLOS) scenarios, where objects are hidden from sight.

FFM exploits the spatial symmetry of the light path from the hidden object to the observer, which allows the system to reconstruct and analyze dynamic hidden objects in the field in an all-optical manner.
By designing the input wavefront, FFM is able to simultaneously project all meshes in the object to their target positions, achieving parallel recovery of hidden objects.
The letter-shaped hidden chromium targets "T", "H" and "U" were used in the experiment, and the exposure time (1 millisecond) and optical power (0.20 mW) were set to achieve rapid imaging of these dynamic targets.
The results show that without the FFM designed wavefront, the image will be severely distorted. While the FFM-designed wavefront was able to recover the shapes of all three letters, the SSIM (structural similarity index) reached 1.0, indicating a high degree of similarity to the original image.
Further, compared with artificial neural network (ANN) in terms of photon efficiency and classification performance, FFM significantly outperforms ANN, especially under low-photon conditions.
Specifically, in situations where the number of photons is limited (such as many reflective or highly diffuse surfaces), FFM is able to adaptively correct wavefront distortion and require fewer photons for accurate classification.
Automatic search for outliers in non-Hermitian systems
FFM methods are not only applicable to free-space optical systems, but can also be extended to the self-design of integrated photonic systems.

The researchers constructed an integrated neural network (a) using symmetric photonic cores configured in series and parallel.
In the experiment, the symmetric core was configured with a variable optical attenuator (VOA) through different levels of injection current to achieve different attenuation coefficients to simulate different weights.
In Figure c, the fidelity of the programmed matrix values in the symmetric core is very high, with standard deviations of time drift of 0.012%, 0.012% and 0.010% respectively, indicating that the matrix values are very stable.
And, the researchers visualized the error for each layer. Comparing the experimental gradient with the theoretical simulation value, the average deviation is 3.5%.
After approximately 100 iterations (epochs), the network reaches convergence.
Experimental results show that under three different symmetry ratio configurations (1.0, 0.75 or 0.5), the classification accuracy of the network is 94.7%, 89.2% and 89.0% respectively.
The classification accuracy obtained by using the neural network using the FFM method is 94.2%, 89.2% and 88.7%.
In contrast, if traditional computer simulation methods are used to design the network, the classification accuracy of the experiment will be lower, respectively 71.7%, 65.8% and 55.0%.
Finally, the researchers also demonstrated that FFM can self-design non-Hermitian systems and achieve traversal of singular points without the need for physical models through numerical simulation.
Non-Hermitian system is a concept in physics, which involves systems in fields such as quantum mechanics and optics, which do not satisfy Hermitian conditions.
Hermitian properties are related to the symmetry of the system and the real number of energy. Non-Hermitian systems do not meet these conditions. They may have some special physical phenomena, such as exceptional points (Exceptional Points), which are the dynamics of the system. Where learning behavior undergoes strange changes at certain points.
To summarize the full article, FFM is a method to implement computationally intensive training processes on physical systems, capable of efficiently executing most machine learning operations in parallel.
For more detailed experimental settings and data set preparation process, please refer to the original article.
Code:
https://zenodo.org/records/10820584
Original text of "Nature":
https://www.nature.com/articles/s41586-024-07687-4
The above is the detailed content of Tsinghua Optics AI appears in Nature! Physical neural network, backpropagation is no longer needed. For more information, please follow other related articles on the PHP Chinese website!
 Tutorial on buying and selling Bitcoin on Huobi.com
Tutorial on buying and selling Bitcoin on Huobi.com
 Solution to slow access speed when renting a US server
Solution to slow access speed when renting a US server
 The role of subnet mask
The role of subnet mask
 What are the development tools?
What are the development tools?
 The meaning of today's headline display volume
The meaning of today's headline display volume
 The difference between mongodb and mysql
The difference between mongodb and mysql
 Registration-free CDN acceleration service
Registration-free CDN acceleration service
 Flutter framework advantages and disadvantages
Flutter framework advantages and disadvantages




