Mitchell Stern and others proposed the prototype concept of speculative sampling in 2018. This approach has since been further developed and refined by various works, including Lookahead Decoding, REST, Medusa and EAGLE, where speculative sampling significantly speeds up the inference process of large language models (LLMs).
An important question is: does speculative sampling in LLM hurt the accuracy of the original model? Let me start with the answer: no.
The standard speculative sampling algorithm is lossless, and this article will prove this through mathematical analysis and experiments.
Mathematical proof
The speculative sampling formula can be defined as follows:
where:
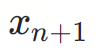is the next token to be predicted. For simplicity, we omit the probability condition. In fact, ? and ? are conditional distributions based on the prefix token sequence 
.
The following is the proof of the losslessness of this formula in the DeepMind paper:
If you feel that reading mathematical equations is too boring, next we will illustrate the proof process through some intuitive diagrams.
This is the distribution diagram of the draft model ? and the basic model ?:
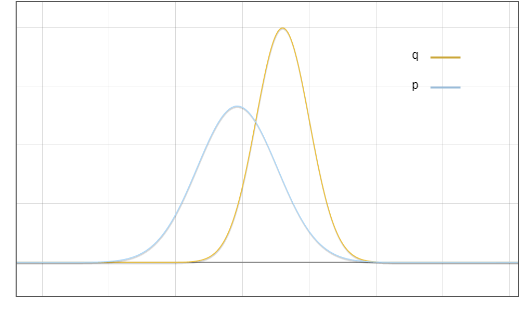
Figure 1: The probability density function of the output distribution of the draft model p and the basic model q
It should be noted that this is just an idealized chart . In practice, what we calculate is a discrete distribution, which looks like this:
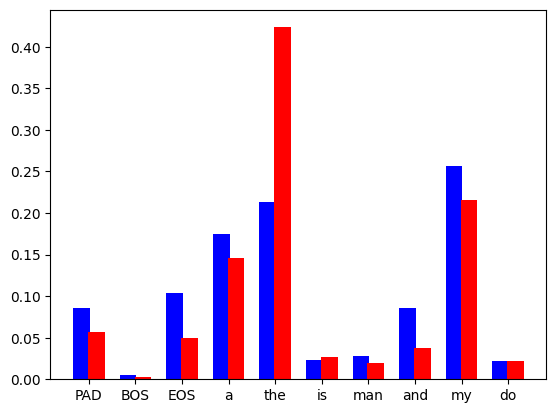
Figure 2: The language model predicts the discrete probability distribution of each token in the vocabulary set, the blue bar is from the draft model, and the red bar is from the base Model.
However, for the sake of simplicity and clarity, we discuss this problem using its continuous approximation.
Now the problem is: we sample from the distribution ? , but we want the end result to be like we sampled from ? . A key idea is: move the probability of the red area to the yellow area:
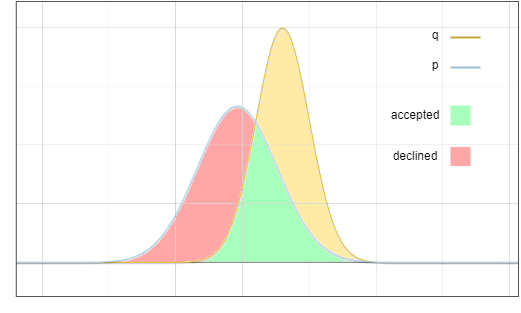
Figure 3: Acceptance and rejection sampling area
Target distribution ? Can be seen as the sum of two parts:
I. Verification Acceptance
There are two independent events in this branch:
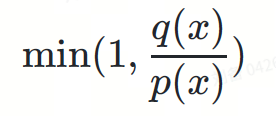
Multiply these probabilities: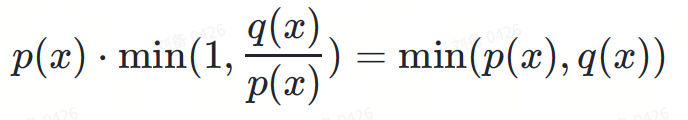 
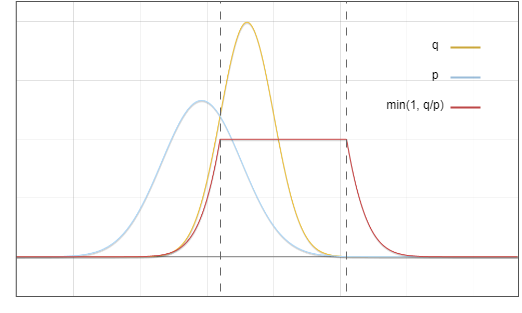
Figure 4: Multiplying the blue and red lines, the result is the green line in Figure 6
II. Validation rejection
in this branch There are also two independent events:
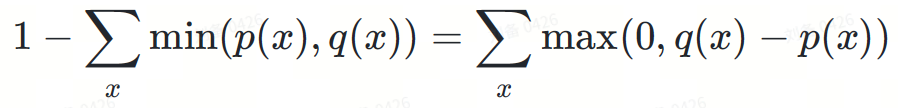
This is an integral value, the value has nothing to do with the specific token x
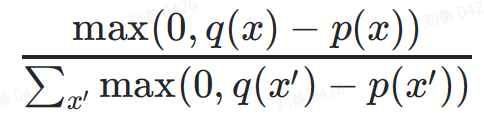
The function of its denominator is to normalize the probability distribution to keep the probability density integral equal to 1.
Two items are multiplied together, and the denominator of the second term is eliminated:
max(0,?(?)−?(?))
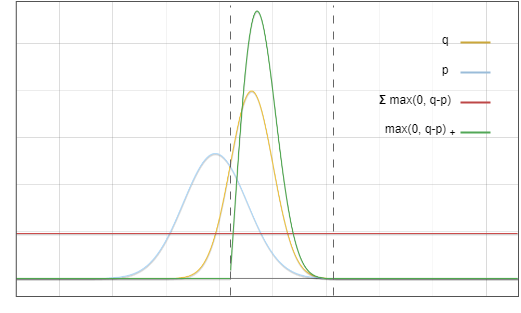
Figure 5. The corresponding functions of the red line and green line in this figure Multiplied together, the result is equal to the red line in Figure 6
Why does the rejection probability happen to be normalized to max(0,?−?)? While it may seem like a coincidence, an important observation here is that the area of the red region in Figure 3 is equal to the area of the yellow region, since the integral of all probability density functions is equal to 1.
Add the two parts I and II: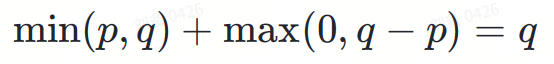 
Finally, we get the target distribution ?.
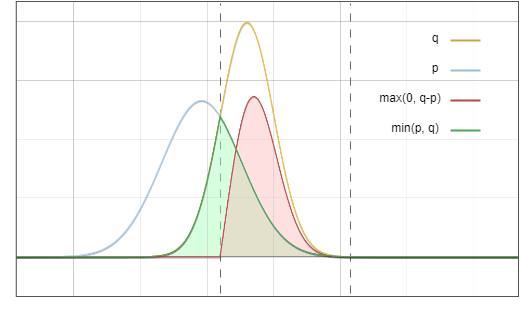
Figure 6. The sum of the green area and the red area is exactly equal to the area below the yellow line
And this is our goal.
Experiments
Although we have proven in principle that speculative sampling is lossless, there may still be bugs in the implementation of the algorithm. Therefore, experimental verification is also necessary.
We conducted experiments on two cases: the deterministic method of greedy decoding and the stochastic method of polynomial sampling.
Greedy Decoding
We ask LLM to generate short stories twice, first using ordinary inference and then using speculative sampling. The sampling temperature is set to 0 for both times. We used the speculative sampling implementation in Medusa. The model weight is medusa-1.0-vicuna-7b-v1.5 and its base model vicuna-7b-v1.5.
After the test run was completed, we got two exactly the same results. The generated text is as follows:
|
User: Please tell a tale about a cyperpunk knight named PPIO keeps a charming llama as his pet. Assistant: Once upon a time, in a world where technology had advanced beyond our wildest dreams, there lived a cyberpunk knight named PPIO. PPIO was a skilled warrior, with advanced cybernetic enhancements that gave him incredible strength and speed. He was also a man of great honor, always striving to do what was right and just . One day, while out on a mission, PPIO stumbled upon a beautiful llama. Despite being a cybernetic being, PPIO had a soft spot for animals and he couldn't resist rescuing the llama from whatever danger it may have been in. From that day on, the llama followed PPIO wherever he went, and the two became fast friends. The llama, whose name was Llama-ella, was a special llama. It had a unique ability to sense when someone was in danger and would let out a loud, distinctive call to alert them to the danger. PPIO was grateful for Llama-ella's ability and the two became an unstoppable team. Together, PPIO and Llama-ella took on all sorts of challenges, from battling cybernetic villains to rescuing innocent people from harm. They were a force to be reckoned with, and their bravery and honor were an inspiration to all who knew them. The situation is more complicated. Most methods of reproducing results in randomized programs use fixed random seeds to exploit the determinism of pseudo-random generators. However, this approach is not suitable for our scenario. Our experiment relies on the law of large numbers: given enough samples, the error between the actual distribution and the theoretical distribution will converge to zero. | We compiled four prompt texts and performed 1,000,000 speculative sampling iterations on the first token generated by LLM under each prompt. The model weights used are
. The statistical results are as follows:
|
結論 投機取樣不會損害大型語言模型的推理精確度。透過嚴格的數學分析和實際實驗，我們證明了標準投機採樣演算法的無損性。其中數學證明說明了投機取樣公式如何保留基礎模型的原始分佈。我們的實驗，包括確定性貪婪解碼和機率多項式取樣，進一步驗證了這些理論發現。貪婪解碼實驗在使用和不使用投機採樣的情況下產生了相同的結果，而多項式採樣實驗表明，在大量樣本中，token分佈的差異可以忽略不計。 這些結果共同證明，投機採樣可以顯著加快 LLM 推理速度，而不會犧牲準確性，為未來更高效、更易於訪問的 AI 系統鋪平了道路。 |
The above is the detailed content of Will speculative sampling lose the inference accuracy of large language models?. For more information, please follow other related articles on the PHP Chinese website!
![[Web front-end] Node.js quick start](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
