Insgesamt10000 bezogener Inhalt gefunden

Ermitteln Sie mithilfe der C++-Programmierung die Anzahl möglicher Hypotenusen- und Flächenpaare eines rechtwinkligen Dreiecks
Artikeleinführung:In diesem Artikel erklären wir, wie man in C++ die Anzahl möglicher Paare aus Hypotenuse und Fläche ermittelt, die ein rechtwinkliges Dreieck bilden. Wir müssen die Anzahl aller möglichen Paare aus Hypotenuse und Fläche (H,A) bestimmen, die ein rechtwinkliges Dreieck bilden, wobei H die Hypotenuse und A die Fläche ist. In diesem Beispiel: ) 2…(1)Wir wissen auch, dass x2+y2=H2…(2)Löse (1)&(2)4*A2=x2(H2-x2)Löse die quadratische Gleichung in x2 und sei D( Diskriminante )>
2023-09-08
Kommentar 0
1118

Wie stelle ich mit FabricJS den Neigungswinkel eines Dreiecks auf der x-Achse ein?
Artikeleinführung:<p>In diesem Tutorial erfahren Sie, wie Sie mit FabricJS den Neigungswinkel auf der x-Achse eines Dreiecks festlegen. Dreieck ist eine der verschiedenen Formen, die FabricJS bereitstellt. Um ein Dreieck zu erstellen, müssen wir eine Instanz der Klasse <em>fabric.Triangle</em> erstellen und sie der Leinwand hinzufügen. </p><p>Wir können unser Dreiecksobjekt anpassen, indem wir seine Größe ändern, eine Hintergrundfarbe hinzufügen oder den Neigungswinkel auf der x-Achse ändern. Dies können wir mit der Eigenschaft <em>skewX</em> erreichen. </p>
2023-09-05
Kommentar 0
881

Wie wäre es mit Operation Delta Kim Luna? Einführung in Operation Delta Kim Luna
Artikeleinführung:Wie wäre es mit Operation Delta Kim Luna? Delta Operations Jin Luna ist ein Aufklärungscharakter, der feindliche Standorte auf dem Schlachtfeld effektiv erkennen kann. Viele Freunde wissen immer noch nicht, wie Delta Operations Golden Luna aussieht. Hier ist eine Einführung in Delta Operations Golden Luna. Wie wäre es mit Operation Delta Jinluna 1. Positionierung: Aufklärung 2. Taktische Ausrüstung „Erkennungspfeil“: Schießt Pfeile ab, die Ziele auf dem Weg erkennen, hat wundersame Auswirkungen. 3. Die taktische Requisite „Elektroschockpfeil“: Verschießt Pfeile, die einen bestimmten Bereich kontinuierlich schocken und dauerhaften Schaden verursachen können. 4. Operator-Spezialität „Hunter Mark“: Sie können den verletzten Feind markieren.
2024-07-19
Kommentar 0
974

Wie sperre ich die vertikale Neigung eines Dreiecks mit FabricJS?
Artikeleinführung:In diesem Tutorial erfahren Sie, wie Sie die vertikale Neigung eines Dreiecks mit FabricJS sperren. So wie wir die Position, Farbe, Deckkraft und Größe des dreieckigen Objekts auf der Leinwand festlegen können, können wir auch festlegen, ob die vertikale Neigung des Objekts gestoppt werden soll. Dies kann mithilfe der lockSkewingY-Eigenschaft erfolgen. Syntax newFabric.Triangle({lockSkewingY:Boolean}:Object) Parameter Optionen (optional) – Dieser Parameter ist ein Objekt, das unserem Dreieck zusätzliche Anpassungen ermöglicht. Mit diesem Parameter können Sie die Farbe, den Cursor, die Strichstärke und viele andere Eigenschaften im Zusammenhang mit dem Objekt mit lockSkewingY als Attribut ändern.
2023-08-31
Kommentar 0
1077
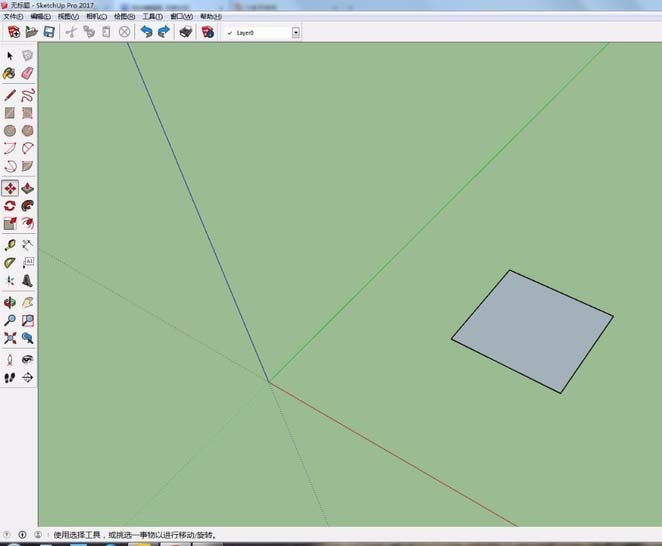
Detaillierter Vorgang zum Entwerfen einer Dreiecksneigung in Sketch Master
Artikeleinführung:Wir öffnen zunächst die Software SketchUp und zeichnen dann ein Rechteck innerhalb des Modells. Dann zeichnen wir die obere Linie des Dreiecks in die Mitte des Rechtecks. Zu diesem Zeitpunkt wählen wir die oberste Linie des Dreiecksbruchs aus und wechseln zum Verschieben-Werkzeug. Ziehen Sie dann die dreieckige, unterbrochene obere Linie und heben Sie sie entlang der blauen Achse nach oben. Im letzten Schritt verbinden wir die untere Linie zu einer Fläche, sodass die Steigung unseres Dreiecks gezeichnet wird.
2024-06-04
Kommentar 0
1190

Einführung in Operator Jin Luna in „Operation Delta'
Artikeleinführung:„Operation Delta“ Jin Luna gehört zur Aufklärungseinheit. Sie kann Einblicke in die Umgebung erhalten, um eine genaue Scharfschützenjagd zu gewährleisten. Da viele Spieler mit diesem Operator nicht vertraut sind, wird Ihnen der Herausgeber den Operator Jin Luna ausführlich vorstellen. Wie wäre es mit Operation Delta Jinluna 1. Positionierung: Aufklärung 2. Taktische Ausrüstung „Erkennungspfeil“: Schießt Pfeile ab, die Ziele auf dem Weg erkennen, hat wundersame Auswirkungen. 3. Die taktische Requisite „Elektroschockpfeil“: Verschießt Pfeile, die einen bestimmten Bereich kontinuierlich schocken und dauerhaften Schaden verursachen können. 4. Operator-Spezialität „Hunter Mark“: Sie können den verletzten Feind markieren.
2024-07-12
Kommentar 0
898

Jian Wang 3 Unbounded Changgemen Xiangzhi seltsame Akupunkturpunkte und Ausgabetechniken-Strategieleitfaden
Artikeleinführung:Wie zeigt man die seltsamen Akupunkturpunkte in Jian Wang 3 Unbounded Changgemen Xiangzhi an? Xiangzhi ist die Heilschildmethode von Changgemen, die dem Team Blutanstieg, Schadensreduzierung und verschiedene Buff-Effekte verleihen kann. Das Folgende ist eine detaillierte Erklärung der seltsamen Punkte von Changgemen Xiangzhi und ihrer Ausgabemethoden. Ich hoffe, dass es meinen Freunden hilfreich sein wird. Changgemen Xiangzhis seltsame Akupunkturpunkte und Ausgabetechniken-Leitfaden 1. Seltsamer Akupunkturpunkt PVP: Yale·Wu → Yingze·Wu → Mei Qing·Wu → Pflaumenblüte Drei Lanes·Wu PVE: Yinghu·Wu → Quyi·Wu → Mei Qing ·Erleuchtung→Drei Pflaumen Blütenbewegungen · Erleuchtung 2. Techniken PVP: Palast (Dian Book)/Sparse Shadow Horizontal (Dian Book)/One Finger Hui Luan (Geheimes Kapitel)/Längenbedeutung (Jue Pian)/Gu Ying Hua Shuang (Qi Juan) ) PVE: Palast (Seltsame Schriftrolle)/One Finger Huiluan (Geheimes Siegel)/Sparse Shadow Horizontal (Seltsame Schriftrolle)/Leng Yi (Geheimes Siegel)/Jiao (Geheimes Siegel)
2024-06-14
Kommentar 0
425

Finden Sie die Hypotenuse einer Zahl in TypeScript
Artikeleinführung:Die längste Seite eines rechtwinkligen Dreiecks und die vom rechten Winkel abgewandte Seite werden Hypotenuse genannt. Der Satz des Pythagoras erklärt, dass das Quadrat der Hypotenuse gleich der Summe der Quadrate der beiden anderen Seiten ist. Wir können diesen Satz verwenden, um es zu bestimmen. Die Formel dieses Theorems lautet c2=a2+b2, wobei c die Hypotenuse darstellt und a und b die beiden Seiten des Dreiecks sind. Mit dem Satz des Pythagoras können Sie den Wert der Hypotenuse schnell bestimmen, wenn die Längen der beiden anderen Seiten des Dreiecks bekannt sind. Zuerst müssen wir die Summe der Quadrate der anderen beiden Seiten bilden, um die Hypotenuse zu erhalten. Der Satz des Pythagoras kann zur Berechnung der Hypotenuse in TypeScript verwendet werden, indem eine Funktion geschrieben wird, die die Länge der beiden kürzeren Seiten als Argumente akzeptiert. Als Ergebnis gibt die Funktion die Hypotenuse zurück. Es gibt eine Bedingung für die Anwendung dieses Theorems und das Finden der Hypotenuse. Das Dreieck muss ein rechtwinkliges Dreieck sein
2023-09-07
Kommentar 0
1217

Gegenseitige Konvertierungsbeziehung trigonometrischer Funktionen
Artikeleinführung:Die Umrechnungsbeziehung zwischen trigonometrischen Funktionen sec (Sekanten) ist der Kehrwert des Sinuswerts csc (Kosekant) ist der Kehrwert des Kosinuswerts sin (Sinus) die Gegenseite/Hypotenuse des rechtwinkligen Dreiecks cos (Kosinus) das Glied/Hypotenuse von das rechtwinklige Dreieck Seitentan (Tangens) die gegenüberliegende Seite/angrenzende Seite eines rechtwinkligen Dreiecks cot (Kotangens) die angrenzende Seite/gegenüberliegende Seite eines rechtwinkligen Dreiecks und die Formel für zwei Winkel sin(A+B)=sinAcosB+cosAsinBsin(A-B) =sinAcosB-cosAsinBcos(A+ B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAta
2024-01-15
Kommentar 0
2754







