Identifizieren Sie Über- und Unteranpassung anhand von Lernkurven

In diesem Artikel wird vorgestellt, wie Überanpassung und Unteranpassung in Modellen für maschinelles Lernen anhand von Lernkurven effektiv identifiziert werden können.

Unteranpassung und Überanpassung

1. Überanpassung

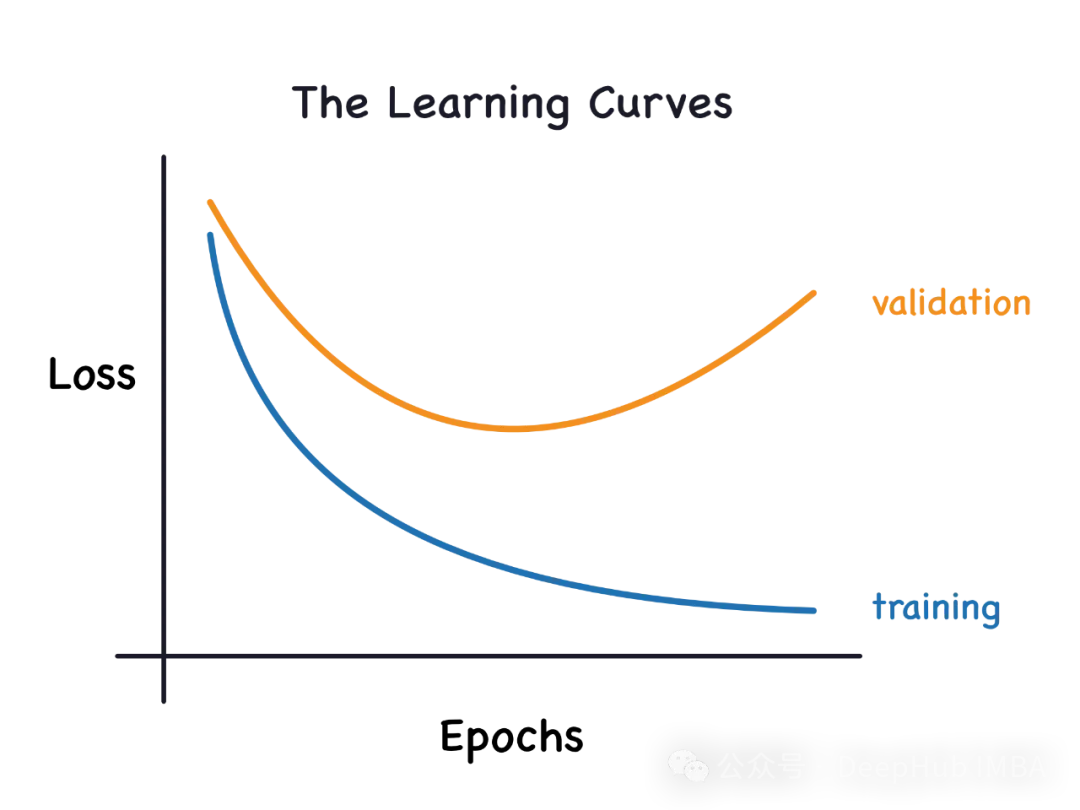
Wenn ein Modell mit den Daten übertrainiert ist, so dass es Rauschen daraus lernt, dann ist das Modell Überanpassung. Ein überangepasstes Modell lernt jedes Beispiel so perfekt, dass es ein unsichtbares/neues Beispiel falsch klassifiziert. Für ein überangepasstes Modell erhalten wir einen perfekten/nahezu perfekten Trainingssatzwert und einen schrecklichen Validierungssatz-/Testwert.

Leicht geändert: „Ursache der Überanpassung: Die Verwendung eines komplexen Modells zur Lösung eines einfachen Problems extrahiert Rauschen aus den Daten. Weil ein kleiner Datensatz als Trainingssatz möglicherweise nicht eine korrekte Darstellung aller Daten darstellt.“ 2. Unteranpassung

Wenn ein Modell die Muster in den Daten nicht richtig lernen kann, sprechen wir von einer Unteranpassung. Unteranpassungsmodelle können nicht jedes Beispiel im Datensatz vollständig lernen. In diesem Fall sehen wir, dass die Fehler sowohl im Trainings- als auch im Validierungssatz gering sind. Dies kann daran liegen, dass das Modell zu einfach ist und nicht über genügend Parameter verfügt, um die Daten anzupassen. Wir können versuchen, die Komplexität des Modells zu erhöhen, die Anzahl der Schichten oder Neuronen zu erhöhen, um das Problem der Unteranpassung zu lösen. Allerdings ist zu beachten, dass mit zunehmender Modellkomplexität auch das Risiko einer Überanpassung steigt.

Gründe, warum es nicht geeignet ist: Verwenden Sie ein einfaches Modell, um ein komplexes Problem zu lösen. Das Modell kann nicht alle Muster in den Daten lernen, oder das Modell lernt die Muster der zugrunde liegenden Daten falsch. Bei der Datenanalyse und beim maschinellen Lernen ist die Modellauswahl sehr wichtig. Die Auswahl des richtigen Modells für Ihr Problem kann die Genauigkeit und Zuverlässigkeit Ihrer Vorhersagen verbessern. Bei komplexen Problemen sind möglicherweise komplexere Modelle erforderlich, um alle Muster in den Daten zu erfassen. Darüber hinaus müssen Sie auch die „Lernkurve“ berücksichtigen. Die Lernkurve stellt die Trainings- und Validierungsverluste der Trainingsprobe selbst dar, indem schrittweise neue Trainingsproben hinzugefügt werden. Kann uns dabei helfen, festzustellen, ob wir zusätzliche Trainingsbeispiele hinzufügen müssen, um den Validierungsscore (Score für unsichtbare Daten) zu verbessern. Wenn das Modell überangepasst ist, kann das Hinzufügen zusätzlicher Trainingsbeispiele die Leistung des Modells bei nicht sichtbaren Daten verbessern. Wenn ein Modell nicht ausreichend fit ist, ist das Hinzufügen von Trainingsbeispielen möglicherweise nicht sinnvoll. Die Methode „learning_curve“ kann aus dem Modul „model_selection“ von Scikit-Learn importiert werden.

from sklearn.model_selection import learning_curve

Wir werden die Verwendung logistischer Regression und Iris-Daten demonstrieren. Erstellen Sie eine Funktion namens „learn_curve“, die zu einem logistischen Regressionsmodell passt und Kreuzvalidierungswerte, Trainingswerte und Lernkurvendaten zurückgibt.

#The function below builds the model and returns cross validation scores, train score and learning curve data def learn_curve(X,y,c): ''' param X: Matrix of input featuresparam y: Vector of Target/Labelc: Inverse Regularization variable to control overfitting (high value causes overfitting, low value causes underfitting)''' '''We aren't splitting the data into train and test because we will use StratifiedKFoldCV.KFold CV is a preferred method compared to hold out CV, since the model is tested on all the examples.Hold out CV is preferred when the model takes too long to train and we have a huge test set that truly represents the universe'''  le = LabelEncoder() # Label encoding the target sc = StandardScaler() # Scaling the input features y = le.fit_transform(y)#Label Encoding the target log_reg = LogisticRegression(max_iter=200,random_state=11,C=c) # LogisticRegression model # Pipeline with scaling and classification as steps, must use a pipelne since we are using KFoldCV lr = Pipeline(steps=(['scaler',sc],['classifier',log_reg]))   cv = StratifiedKFold(n_splits=5,random_state=11,shuffle=True) # Creating a StratifiedKFold object with 5 folds cv_scores = cross_val_score(lr,X,y,scoring="accuracy",cv=cv) # Storing the CV scores (accuracy) of each fold   lr.fit(X,y) # Fitting the model  train_score = lr.score(X,y) # Scoring the model on train set  #Building the learning curve train_size,train_scores,test_scores =learning_curve(estimator=lr,X=X,y=y,cv=cv,scoring="accuracy",random_state=11) train_scores = 1-np.mean(train_scores,axis=1)#converting the accuracy score to misclassification rate test_scores = 1-np.mean(test_scores,axis=1)#converting the accuracy score to misclassification rate lc =pd.DataFrame({"Training_size":train_size,"Training_loss":train_scores,"Validation_loss":test_scores}).melt(id_vars="Training_size") return {"cv_scores":cv_scores,"train_score":train_score,"learning_curve":lc}

Der obige Code ist sehr einfach, es ist unser täglicher Trainingsprozess. Jetzt beginnen wir mit der Einführung der Lernkurve.

1. Lernkurve des Anpassungsmodells Funktion „learn_curve“ Ein gut passendes Modell erhält man, indem man die Anti-Regularisierungsvariable/den Anti-Regularisierungsparameter „c“ auf 1 setzt (d. h. wir führen keine Regularisierung durch).

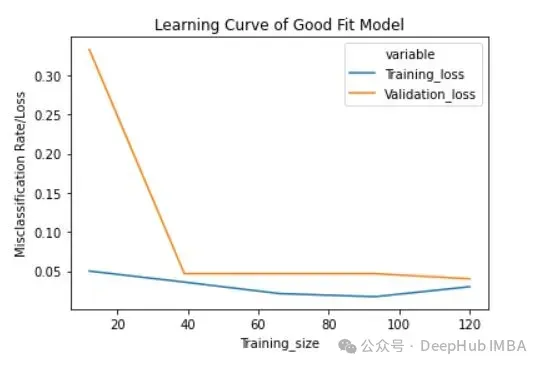
lc = learn_curve(X,y,1) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Deep HUB Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])}\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of Good Fit Model") plt.ylabel("Misclassification Rate/Loss");

Trainingsverlust (blau): Die Lernkurve eines gut angepassten Modells nimmt mit zunehmender Anzahl von Trainingsbeispielen allmählich ab und wird flacher, was darauf hinweist, dass das Hinzufügen weiterer Trainingsbeispiele die Leistung des Modells nicht verbessern kann die Trainingsdaten.

Validierungsverlust (gelb): Die Lernkurve eines gut angepassten Modells weist zu Beginn einen hohen Validierungsverlust auf, der mit zunehmender Anzahl der Trainingsproben allmählich abnimmt und abflacht, was darauf hinweist, dass Sie umso mehr Proben haben kann mehr Muster lernen, was für „unsichtbare“ Daten hilfreich sein wird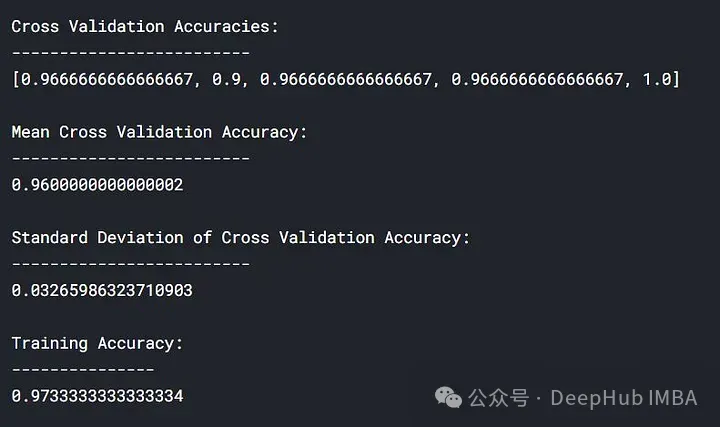

Schließlich können Sie auch sehen, dass nach dem Hinzufügen einer angemessenen Anzahl von Trainingsbeispielen der Trainingsverlust und der Validierungsverlust nahe beieinander liegen.

2. Lernkurve des Überanpassungsmodells

Wir verwenden die Funktion „learn_curve“, um den hohen Wert des Überanpassungsmodells zu erhalten („c“-Wert führt zu Überanpassung).

lc = learn_curve(X,y,10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Deep HUB Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (High Variance)\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Overfit Model") plt.ylabel("Misclassification Rate/Loss");

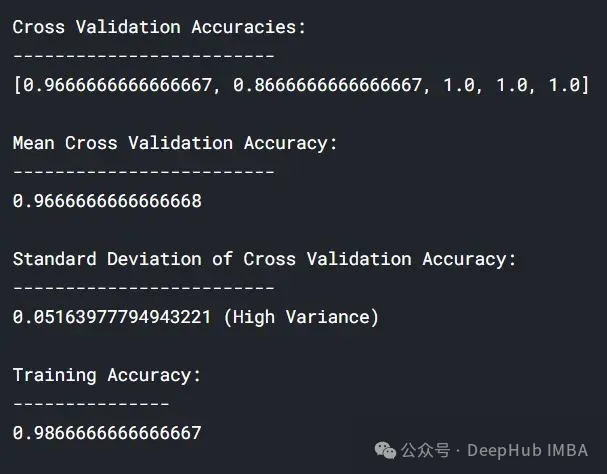
与拟合模型相比，交叉验证精度的标准差较高。

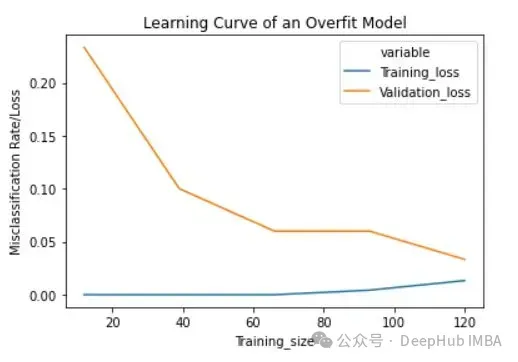
过拟合模型的学习曲线一开始的训练损失很低，随着训练样例的增加，学习曲线逐渐增加，但不会变平。过拟合模型的学习曲线在开始时具有较高的验证损失，随着训练样例的增加逐渐减小并且不趋于平坦，说明增加更多的训练样例可以提高模型在未知数据上的性能。同时还可以看到，训练损失和验证损失彼此相差很远，在增加额外的训练数据时，它们可能会彼此接近。

3、欠拟合模型的学习曲线

将反正则化变量/参数' c '设置为1/10000来获得欠拟合模型(' c '的低值导致欠拟合)。

lc = learn_curve(X,y,1/10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (Low variance)\n\n\ Training Deep HUB Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Underfit Model") plt.ylabel("Misclassification Rate/Loss");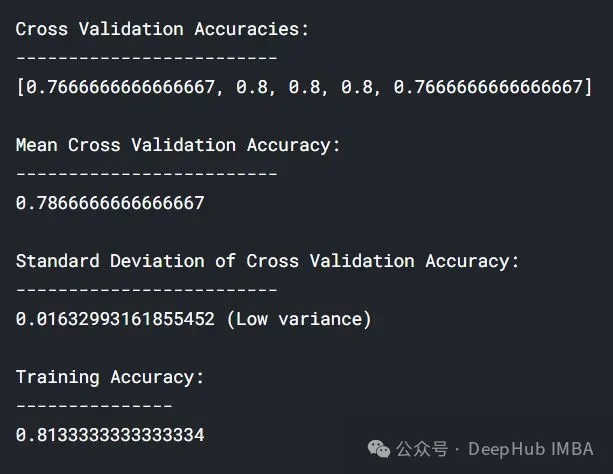

与过拟合和良好拟合模型相比，交叉验证精度的标准差较低。

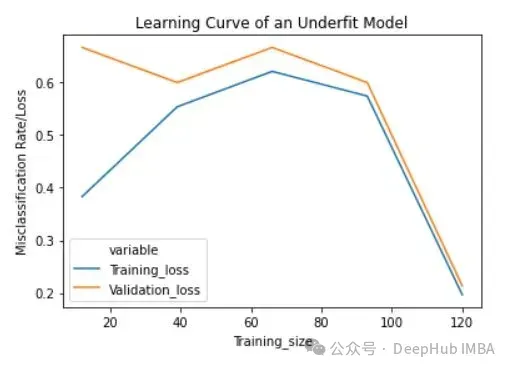
欠拟合模型的学习曲线在开始时具有较低的训练损失，随着训练样例的增加逐渐增加，并在最后突然下降到任意最小点(最小并不意味着零损失)。这种最后的突然下跌可能并不总是会发生。这表明增加更多的训练样例并不能提高模型在未知数据上的性能。

总结

在机器学习和统计建模中，过拟合（Overfitting）和欠拟合（Underfitting）是两种常见的问题，它们描述了模型与训练数据的拟合程度如何影响模型在新数据上的表现。

分析生成的学习曲线时，可以关注以下几个方面：

• 欠拟合：如果学习曲线显示训练集和验证集的性能都比较低，或者两者都随着训练样本数量的增加而缓慢提升，这通常表明模型欠拟合。这种情况下，模型可能太简单，无法捕捉数据中的基本模式。
• 过拟合：如果训练集的性能随着样本数量的增加而提高，而验证集的性能在一定点后开始下降或停滞不前，这通常表示模型过拟合。在这种情况下，模型可能太复杂，过度适应了训练数据中的噪声而非潜在的数据模式。

根据学习曲线的分析，你可以采取以下策略进行调整：

• 对于欠拟合：

• 增加模型复杂度，例如使用更多的特征、更深的网络或更多的参数。
• 改善特征工程，尝试不同的特征组合或转换。
• 增加迭代次数或调整学习率。

• 对于过拟合：

• 使用正则化技术（如L1、L2正则化）。

• 减少模型的复杂性，比如减少参数数量、层数或特征数量。

• 增加更多的训练数据。

• 应用数据增强技术。

• 使用早停（early stopping）等技术来避免过度训练。

通过这样的分析和调整，学习曲线能够帮助你更有效地优化模型，并提高其在未知数据上的泛化能力。