
Kernel Model Gaußian Processes (KMGPs) sind hochentwickelte Werkzeuge zur Bewältigung der Komplexität verschiedener Datensätze. Es erweitert das Konzept traditioneller Gaußscher Prozesse um Kernelfunktionen. In diesem Artikel werden die theoretischen Grundlagen, praktischen Anwendungen und Herausforderungen von KMGPs ausführlich erörtert.
Der Kernelmodell-Gauß-Prozess ist eine Erweiterung des traditionellen Gauß-Prozesses und wird beim maschinellen Lernen und in der Statistik verwendet. Bevor Sie kmgp verstehen, müssen Sie die Grundkenntnisse des Gaußschen Prozesses beherrschen und dann die Rolle des Kernelmodells verstehen.
Gaußsche Prozesse sind Sätze von Zufallsvariablen mit einer begrenzten Anzahl von Variablen, die gemeinsam durch Gauß verteilt werden und zur Definition von Funktionswahrscheinlichkeitsverteilungen verwendet werden.
Der Gaußsche Prozess wird häufig bei Regressions- und Klassifizierungsaufgaben beim maschinellen Lernen verwendet und kann zur Anpassung der Wahrscheinlichkeitsverteilung von Daten verwendet werden.
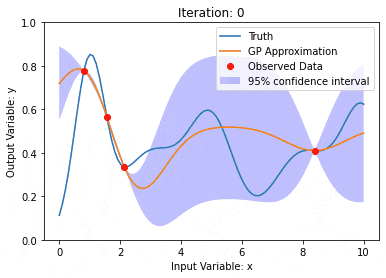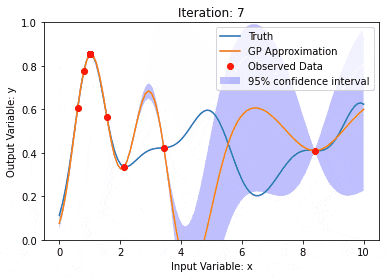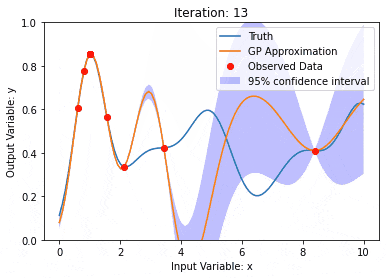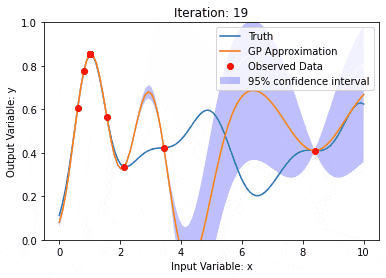
Ein wichtiges Merkmal von Gaußschen Prozessen ist die Fähigkeit, Unsicherheitsschätzungen und -vorhersagen bereitzustellen, was beim Verständnis der Zuverlässigkeit einer Vorhersage sehr nützlich ist und ebenso wichtig ist wie die Vorhersage selbst.
In einem Gaußschen Prozess wird die Kernelfunktion (oder Kovarianzfunktion) verwendet, um die Ähnlichkeit zwischen verschiedenen Datenpunkten zu messen. Die Kernelfunktion nimmt zwei Eingaben entgegen und berechnet den Ähnlichkeitswert zwischen ihnen.
Es gibt verschiedene Arten von Kerneln wie lineare, polynomiale und radiale Basisfunktionen (RBF). Jeder Kern weist unterschiedliche Eigenschaften auf und der geeignete Kern kann je nach Problem ausgewählt werden.
In Gaußschen Prozessen ist die Kernel-Modellierung der Prozess der Auswahl und Optimierung von Kernel-Funktionen, um die zugrunde liegenden Muster in den Daten bestmöglich zu erfassen. Dieser Schritt ist sehr wichtig, da die Auswahl und Konfiguration des Kernels die Leistung des Gaußschen Prozesses erheblich beeinflussen kann.
KMGPs ist eine Erweiterung des Standard-GP (Gaussian Process) und konzentriert sich auf die Anwendung von Kernelfunktionen. Im Vergleich zu Standard-GPs legen KMGPs mehr Wert auf die Anpassung komplexer oder benutzerdefinierter Kernelfunktionen an bestimmte Datentypen oder Probleme. Dieser Ansatz ist besonders nützlich, wenn die Daten komplex sind und Standardkernelfunktionen die zugrunde liegenden Beziehungen nicht erfassen können. Das Entwerfen und Optimieren von Kernelfunktionen in KMGPs stellt jedoch eine Herausforderung dar und erfordert häufig umfassende Domänenkenntnisse und Berufserfahrung in der Problemdomäne und der statistischen Modellierung.
Der Kernel-Modell-Gauß-Prozess ist ein hochentwickeltes Werkzeug für das statistische Lernen und bietet eine flexible und leistungsstarke Möglichkeit, komplexe Datensätze zu modellieren. Sie werden besonders für ihre Fähigkeit geschätzt, Unsicherheitsschätzungen bereitzustellen und für ihre Anpassungsfähigkeit, verschiedene Datentypen durch benutzerdefinierte Abstimmungen abzugleichen.
Gut gestaltete Kernel in KMGP können komplexe Phänomene wie nichtlineare Trends, Periodizität und Heteroskedastizität (unterschiedliche Rauschpegel) in den Daten modellieren. Daher sind fundierte Domänenkenntnisse und ein umfassendes Verständnis der statistischen Modellierung erforderlich.
KMGP hat Anwendungen in vielen Bereichen. In der Geostatistik modellieren sie räumliche Daten, um die zugrunde liegende geografische Variation zu erfassen. Im Finanzwesen werden sie verwendet, um Aktienkurse vorherzusagen, was die Instabilität und Komplexität der Finanzmärkte erklärt. In der Robotik und in Steuerungssystemen modellieren und prognostizieren KMGPs das Verhalten dynamischer Systeme unter Unsicherheit.
Wir verwenden einen synthetischen Datensatz, um ein vollständiges Python-Codebeispiel zu erstellen. Hier verwenden wir eine Bibliothek GPy, eine Bibliothek in Python, die auf die Verarbeitung von Gaußschen Prozessen spezialisiert ist.
pip install numpy matplotlib GPy
Bibliothek importieren
import numpy as np import matplotlib.pyplot as plt import GPy
Dann erstellen wir einen synthetischen Datensatz mit Numpy.
X = np.linspace(0, 10, 100)[:, None] Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
Definieren und trainieren Sie ein Gaußsches Prozessmodell mit GPy
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.) model = GPy.models.GPRegression(X, Y, kernel) model.optimize(messages=True)
Nachdem wir das Modell trainiert haben, werden wir es verwenden, um Vorhersagen für den Testdatensatz zu treffen. Zeichnen Sie dann ein Diagramm, um die Leistung des Modells zu visualisieren.
X_test = np.linspace(-2, 12, 200)[:, None] Y_pred, Y_var = model.predict(X_test) plt.figure(figsize=(10, 5)) plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction') plt.fill_between(X_test.flatten(), (Y_pred - 2*np.sqrt(Y_var)).flatten(), (Y_pred + 2*np.sqrt(Y_var)).flatten(), alpha=0.5, color='pink', label='Confidence Interval') plt.scatter(X, Y, c='b', label='Training Data') plt.xlabel('X') plt.ylabel('Y') plt.title('Kernel Modeled Gaussian Process Regression') plt.legend() plt.show()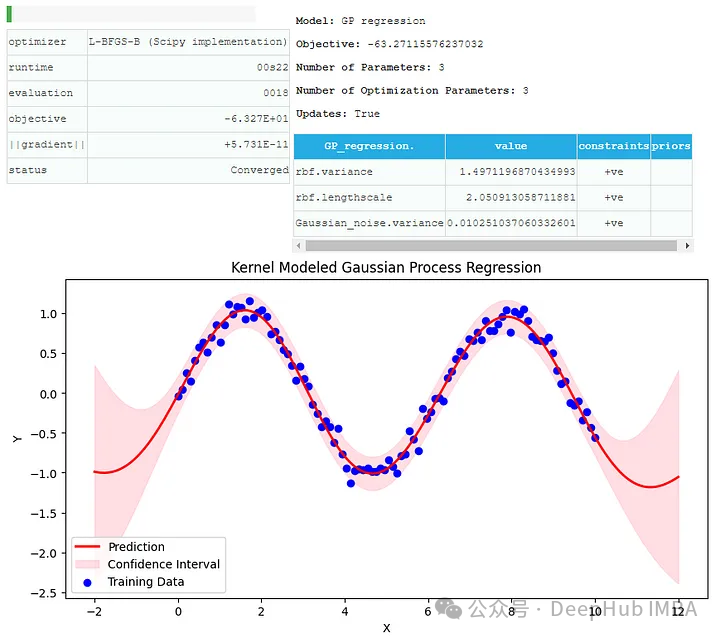
Hier wenden wir das Gaußsche Prozessregressionsmodell mit dem RBF-Kernel an und können die Vorhersage- und Trainingsdaten sowie das Konfidenzintervall sehen.
Der Gaußsche Prozess des Kernelmodells stellt einen großen Fortschritt im Bereich des statistischen Lernens dar und bietet einen flexiblen und leistungsstarken Rahmen zum Verständnis komplexer Datensätze. GPy enthält im Grunde auch alle Kernelfunktionen, die wir sehen können:
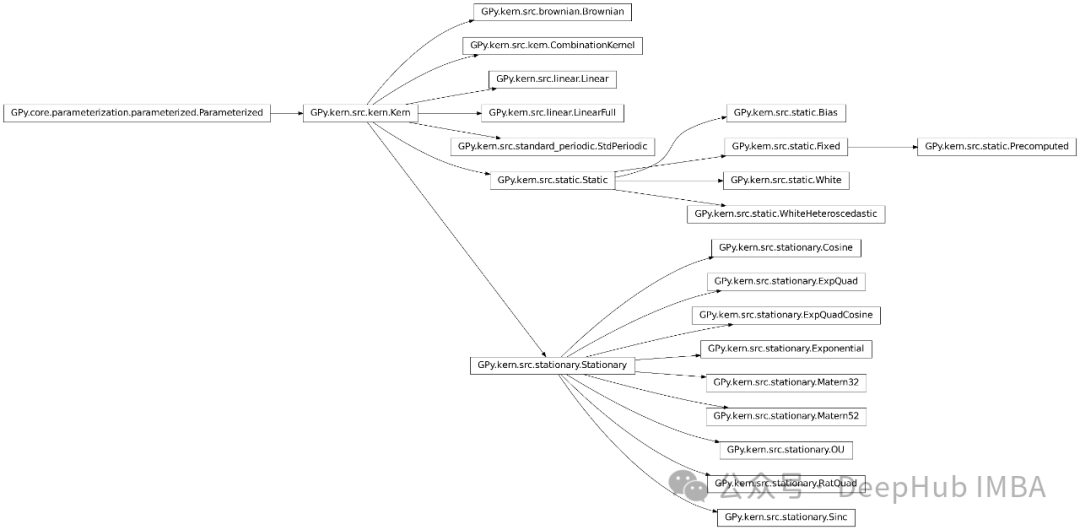
Für verschiedene Daten müssen Sie verschiedene Kernelfunktions-Kernel-Hyperparameter auswählen. Hier ist der offizielle GPy A-Ablauf Diagramm ist gegeben
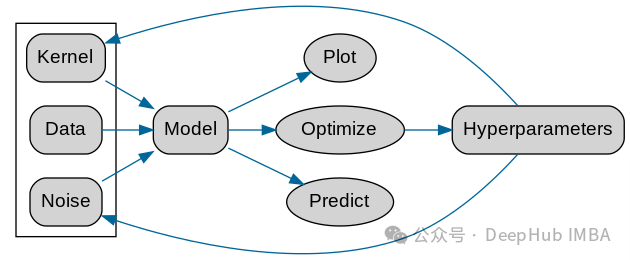
Das obige ist der detaillierte Inhalt vonDatenmodellierung mit Kernel Model Gaußian Processes (KMGPs). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Was soll ich tun, wenn Chaturbate hängen bleibt?
Was soll ich tun, wenn Chaturbate hängen bleibt?
 So fügen Sie ein Video in HTML ein
So fügen Sie ein Video in HTML ein
 Methoden zur Behebung von Schwachstellen in Computersystemen
Methoden zur Behebung von Schwachstellen in Computersystemen
 Die Webseite kann nicht geöffnet werden
Die Webseite kann nicht geöffnet werden
 Was bedeutet Metaverse Concept Stock?
Was bedeutet Metaverse Concept Stock?
 js-String in Array umwandeln
js-String in Array umwandeln
 So lösen Sie devc-chinesische verstümmelte Zeichen
So lösen Sie devc-chinesische verstümmelte Zeichen
 Historisches Bitcoin-Preisdiagramm
Historisches Bitcoin-Preisdiagramm




