Hallo zusammen, mein Name ist Yuan Jianhao und ich freue mich sehr, zur Heart of Autonomous Driving-Plattform zu kommen, um unsere Arbeit zur Radarpositionserkennung auf der IROS2023 zu teilen.
Die Positionierung mithilfe von frequenzmoduliertem Dauerstrichradar (FMCW) gewinnt aufgrund seiner inhärenten Widerstandsfähigkeit gegenüber anspruchsvollen Umgebungen zunehmend an Bedeutung. Allerdings erfordern komplexe Artefakte des Radarmessprozesses entsprechende Unsicherheitsschätzungen – um eine sichere und zuverlässige Anwendung dieser vielversprechenden Sensormodalität zu gewährleisten. In dieser Arbeit schlagen wir ein Kartenverwaltungssystem für mehrere Sitzungen vor, das auf der Grundlage der erlernten Varianzeigenschaften im Einbettungsraum eine „optimale“ Karte zur weiteren Lokalisierung erstellt. Unter Verwendung derselben Varianzeigenschaft schlagen wir auch eine neue Methode vor, um Positionierungsabfragen, die möglicherweise falsch sind, introspektiv abzulehnen. Zu diesem Zweck wenden wir robustes geräuschbewusstes metrisches Lernen an, das sowohl kurzzeitige Schwankungen der Radardaten entlang des Fahrwegs (zur Datenerweiterung) ausnutzt als auch nachgelagerte Unsicherheiten bei der metrischen raumbasierten Positionsidentifizierung vorhersagt. Wir demonstrieren die Wirksamkeit unseres Ansatzes durch umfangreiche Kreuzvalidierungstests an den Oxford Radar RobotCar- und MulRan-Datensätzen. Hier übertreffen wir den aktuellen Stand der Technik bei der Radarpositionsidentifizierung und anderen unsicherheitsbewussten Methoden mit nur einer einzigen Abfrage des nächsten Nachbarn. Wir zeigen auch eine Leistungssteigerung in einer schwierigen Testumgebung bei der Ablehnung von Abfragen aufgrund von Unsicherheit, die wir bei konkurrierenden unsicheren Standorterkennungssystemen nicht beobachtet haben.
Standorterkennung und Lokalisierung sind wichtige Aufgaben im Bereich der Robotik und autonomen Systeme, da sie es Systemen ermöglichen, ihre Umgebung zu verstehen und darin zu navigieren. Herkömmliche visuelle Standorterkennungsmethoden sind häufig anfällig für Änderungen der Umgebungsbedingungen wie Beleuchtung, Wetter und Okklusion, was zu Leistungseinbußen führt. Um dieses Problem anzugehen, besteht ein zunehmendes Interesse daran, FMCW-Radar als robuste Sensoralternative in diesem schwierigen Umfeld einzusetzen.
Bestehende Arbeiten haben die Wirksamkeit handgefertigter und lernbasierter Merkmalsextraktionsmethoden für die FMCW-Radarpositionserkennung gezeigt. Trotz des Erfolgs bestehender Arbeiten ist der Einsatz dieser Methoden in sicherheitskritischen Anwendungen wie dem autonomen Fahren immer noch durch Schätzungen der Kalibrierungsunsicherheit begrenzt. In diesem Bereich müssen die folgenden Punkte berücksichtigt werden:
Überblick über den Systemprozess
In der Offline-Phase verwenden wir ein variierendes kontrastives Lernrahmenwerk, um einen verborgenen Einbettungsraum mit geschätzter Unsicherheit zu erlernen, sodass Radarscans von ähnlichen topologischen Standorten nahe beieinander liegen und umgekehrt. In der Online-Phase haben wir zwei auf Unsicherheiten basierende Mechanismen entwickelt, um kontinuierlich gesammelte Radarscans für Schlussfolgerungen und Kartenkonstruktionen zu verarbeiten. Für wiederholte Durchquerungen derselben Route pflegen wir aktiv ein integriertes Kartenwörterbuch, indem wir sehr unsichere Scans durch sicherere Scans ersetzen. Für Abfragescans mit geringer Unsicherheit rufen wir basierend auf der metrischen Raumentfernung passende Kartenscans aus dem Wörterbuch ab. Im Gegensatz dazu lehnen wir Vorhersagen für Scans mit hoher Unsicherheit ab.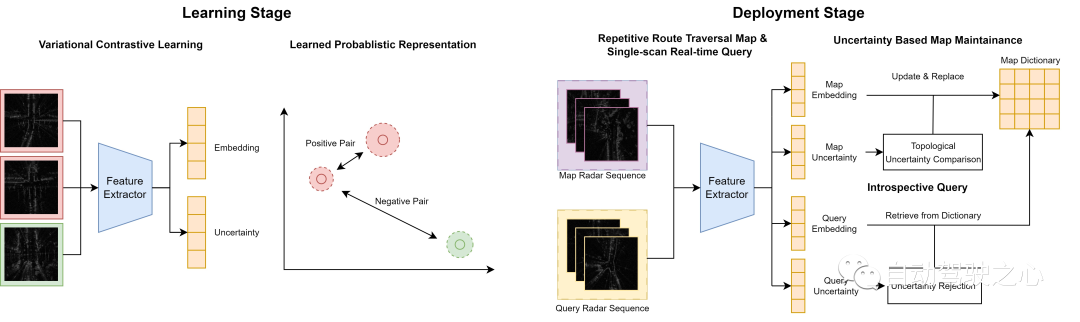 
Einführung in die Methode „Off the Radar“
Unsicherheitsbewusster kontrastiver Lernrahmen.
Überblick über das variierende kontrastive Lerngerüst, basierend auf [^Lin2018dvml]. Lernen Sie einen metrischen Raum durch eine Encoder-Decoder-Struktur mit zwei reparametrisierten Teilen: einer deterministischen Einbettung und einem Satz von Parametern zur Identifikation modelliert eine multivariate Gaußsche Verteilung mit ihrer Varianz als Unsicherheitsmaß. Ganzheitliches Lernen wird sowohl durch Rekonstruktion als auch durch Kontrastverluste vorangetrieben, um informative und differenzierte verborgene Darstellungen von Radarscans sicherzustellen.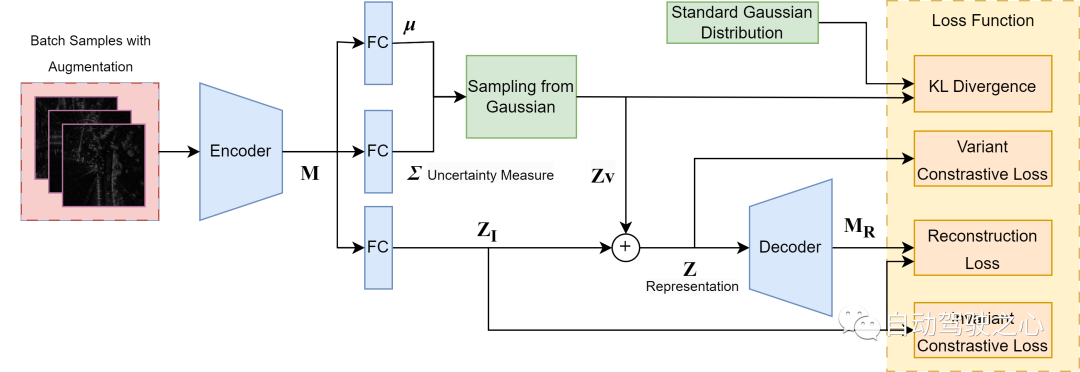 
Die Arbeit in diesem Abschnitt ist sowohl ein wichtiger Wegbereiter unseres Kernbeitrags als auch eine neuartige Integration von tiefem Variationsmetriklernen mit Radarpositionserkennung sowie eine neue Möglichkeit zur Charakterisierung von Unsicherheit bei der Positionserkennung. Wie in der Abbildung gezeigt, verwenden wir eine Struktur, um die Einbettung des Radarscans in einen rauschinduzierten Variablenteil zu zerlegen, der die Varianz von Unsicherheitsquellen erfasst, die nichts mit der Vorhersage zu tun haben, und einen semantisch invarianten Teil für die Szenendarstellung. Der variable Teil wird später aus einer vorherigen multivariaten Gaußschen Verteilung mit gleichen Quadraten entnommen und zum Invarianzteil addiert, um die Gesamtdarstellung zu bilden. Die variable Ausgabe wird direkt als Unsicherheitsmaß verwendet. Wir gehen davon aus, dass wir nur aleatorische Unsicherheiten in Modellvorhersagen, die durch inhärente Unschärfe und Zufälligkeit in den Daten verursacht werden, als Hauptquelle der Unsicherheit betrachten. Insbesondere bei Radarscans kann dies auf Speckle-Rauschen, Sättigung und vorübergehende Verdeckungen zurückzuführen sein. Standardmäßige metrische Lernmethoden neigen unabhängig von der gewählten Verlustfunktion dazu, identische Einbettungen zwischen Paaren positiver Beispiele zu erzwingen und gleichzeitig die potenzielle Varianz zwischen ihnen zu ignorieren. Dies kann jedoch dazu führen, dass das Modell gegenüber kleinen Merkmalen unempfindlich ist und die Trainingsverteilung zu stark anpasst. Um die Rauschvarianz zu modellieren, verwenden wir daher die zusätzliche probabilistische Varianzausgabe in der Struktur, um die aleatorische Unsicherheit abzuschätzen. Um eine solche rauschbewusste, Radar-bewusste Darstellung zu erstellen, verwenden wir vier Verlustfunktionen, um das gesamte Training zu leiten.
1) Invarianter Kontrastverlust bei der deterministischen Darstellung (Z_I), um aufgabenirrelevantes Rauschen von der Radarsemantik zu trennen, damit die invariante Einbettung ausreichend kausale Informationen enthält; und
2) Variabler Kontrastverlust Bei der Gesamtdarstellung (Z ), etablieren Sie einen aussagekräftigen metrischen Raum. Beide Kontrastverluste nehmen die folgende Form an.
Eine der Chargen besteht aus m Stichproben und einer zeitlich angenäherten Rahmenerweiterung der synthetischen Rotation unter Verwendung der „Rotate“-Strategie, die lediglich eine Rotationserweiterung für Rotationsinvarianz ist. Unser Ziel ist es, die Wahrscheinlichkeit zu maximieren, dass eine erweiterte Stichprobe als Originalinstanz erkannt wird, und gleichzeitig die Wahrscheinlichkeit des Umkehrfalls zu minimieren.
wobei die Einbettung (Z) (Z_I) oder (Z) ist, wie in den Gleichungen 1) und 2) beschrieben.
3) Kullback-Leibler (KL)-Divergenz Zwischen der erlernten Gaußschen Verteilung und der standardmäßigen isotropen multivariaten Gaußschen Verteilung ist dies unsere a priori Annahme von Datenrauschen. Dies stellt die gleiche Verteilung des Rauschens über alle Proben sicher und bietet eine statische Referenz für den Absolutwert der Variablenausgabe.
4) Der Rekonstruktionsverlust liegt zwischen der extrahierten Feature-Map (M) und der Decoder-Ausgabe (M_R), was dazu führt, dass die Gesamtdarstellung (Z) genügend Informationen aus dem ursprünglichen Radarscan enthält, um rekonstruiert zu werden. Wir rekonstruieren jedoch nur eine Feature-Map mit niedrigerer Dimension anstelle einer Radarscan-Rekonstruktion auf Pixelebene, um den Rechenaufwand im Decodierungsprozess zu reduzieren.
Während die gewöhnliche VAE-Struktur, die nur durch KL-Divergenz und Rekonstruktionsverlust angetrieben wird, auch latente Varianz liefert, wird sie aufgrund ihres bekannten posterioren Kollaps und der verschwindenden Varianzprobleme als unzuverlässig für die Unsicherheitsschätzung angesehen. Diese Ineffektivität ist hauptsächlich auf das Ungleichgewicht der beiden Verluste während des Trainings zurückzuführen: Wenn die KL-Divergenz dominiert, wird der latente Raum posterior gezwungen, dem vorherigen zu entsprechen, während, wenn der Rekonstruktionsverlust dominiert, die latente Varianz auf Null gedrückt wird. In unserem Ansatz erreichen wir jedoch ein stabileres Training, indem wir einen variablen Kontrastverlust als zusätzlichen Regularisierer einführen, wobei die Varianz so gesteuert wird, dass robuste Grenzen zwischen Clusterzentren im metrischen Raum aufrechterhalten werden. Als Ergebnis erhalten wir eine zuverlässigere zugrunde liegende räumliche Varianz, die die zugrunde liegende aleatorische Unsicherheit bei der Radarwahrnehmung widerspiegelt. Wir haben uns dafür entschieden, die Vorteile unseres spezifischen Ansatzes zur Lernunsicherheit in einer Umgebung mit merkmalsvergrößernden Verlusten zu demonstrieren. In diesem Bereich verwenden moderne Techniken zur Radarpositionserkennung bereits Verluste mit vielen (d. h. mehr als 2) negativen Abtastwerten, weshalb wir auf dieser Basis erweitern.
Die kontinuierliche Kartenpflege ist ein wichtiges Merkmal von Online-Systemen, da wir darauf abzielen, die beim autonomen Fahrzeugbetrieb gewonnenen Scandaten vollständig zu nutzen und die Karte rekursiv zu verbessern. Der Prozess zum Zusammenführen neuer Radarscans in einer übergeordneten Karte, die aus zuvor durchlaufenen Scans besteht, ist wie folgt. Jeder Radarscan wird durch eine versteckte Darstellung und eine Unsicherheitsmetrik dargestellt. Während des Zusammenführungsprozesses suchen wir für jeden neuen Scan nach passenden positiven Proben mit einem topologischen Abstand unterhalb eines Schwellenwerts. Wenn der neue Scan eine geringere Unsicherheit aufweist, wird er in die übergeordnete Karte integriert und ersetzt den passenden Scan, andernfalls wird er verworfen.
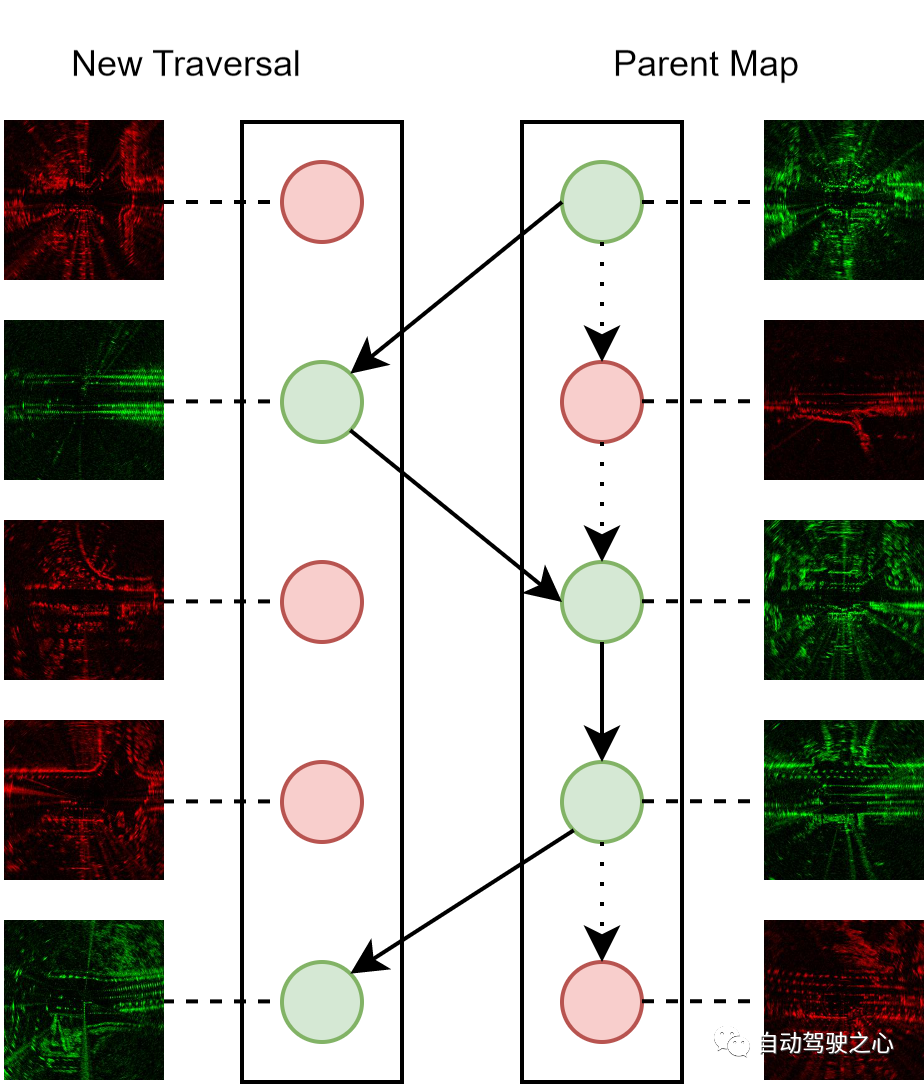
Kartenwartungsdiagramm: Rote und grüne Knoten stellen Radarscans mit höherer bzw. niedrigerer Unsicherheit dar. Wir pflegen stets eine übergeordnete Karte als Positionierungsreferenz für jeden Standort, die nur aus Scans mit der geringsten Unsicherheit besteht. Beachten Sie, dass die gestrichelten Kanten den Anfangszustand der übergeordneten Karte darstellen und die durchgezogenen Kanten aktualisierte Versionen der übergeordneten Karte darstellen.
Durch die iterative Durchführung des Wartungsprozesses können wir die Qualität der integrierten übergeordneten Karte schrittweise verbessern. Daher kann der Wartungsalgorithmus als effektive Online-Bereitstellungsstrategie dienen, da er kontinuierlich mehrere Erfahrungen mit derselben Routendurchquerung nutzt, um die Erkennungsleistung zu verbessern und gleichzeitig eine konstante Größe der übergeordneten Karte beizubehalten, was zu budgetierten Rechen- und Speicherkosten führt.
Introspektive Abfrage
Aufgrund der Modellunsicherheit bei Messungen aus der Standard-Gauß-Verteilung liegt die geschätzte Varianz für alle Dimensionen nahe bei 1. Daher können wir den Maßstab und die Auflösung der Unsicherheitszurückweisung mithilfe von zwei Hyperparametern, Delta und N, vollständig definieren. Der resultierende Schwellenwert T ist wie folgt definiert:
Bei einem Scan mit m-dimensionaler latenter Varianz mitteln wir über alle Dimensionen, was zu einem skalaren Unsicherheitsmaß führt Abfragescans, bei denen die Varianz über einem definierten Schwellenwert liegt, werden zur Identifizierung abgelehnt. Bestehende Methoden wie STUN und MC Dropout unterteilen den Unsicherheitsbereich einer Probencharge dynamisch in Schwellenwerte. Dies erfordert jedoch mehrere Stichproben während der Inferenz und kann zu einer instabilen Ablehnungsleistung führen, insbesondere wenn nur eine kleine Anzahl von Stichproben vorhanden ist. Im Gegensatz dazu liefert unsere statische Schwellenwertstrategie stichprobenunabhängige Schwellenwerte und sorgt für eine konsistente Schätzung und Ablehnung der Unsicherheit bei einem Scan. Diese Funktion ist für den Echtzeiteinsatz von Standorterkennungssystemen von entscheidender Bedeutung, da Radarscans Bild für Bild während der Fahrt erfasst werden.
Experimentelle Details
Dieser Artikel verwendet zwei Datensätze: 1) Oxford Radar RobotCar und 2) MulRan. Beide Datensätze verwenden das CTS350-X Navtech FMCW-Scanning-Radar. Das Radarsystem arbeitet im Bereich von 76 GHz bis 77 GHz und kann bis zu 3768 Entfernungsmessungen mit einer Auflösung von 4,38 cm erzeugen. Die Erkennungsleistung des
erfolgt durch Vergleich mit mehreren bestehenden Methoden, einschließlich der ursprünglichen VAE, der von Gadd
et al vorgeschlagenen hochmodernen Methode zur Radarstandortidentifizierung namens BCRadar. und die nicht lernbasierte Methode RingKey (Teil von ScanContext, ohne Rotationsverfeinerung). Darüber hinaus wird die Leistung mit MC Dropout und STUN verglichen, die als Basislinien für die unsichere Ortserkennung dienen. AblationsstudieUm die Wirksamkeit unserer vorgeschlagenen introspektiven Abfrage- (Q) und Kartenwartungsmodule (M) zu bewerten, haben wir eine Ablationsstudie durchgeführt, indem wir verschiedene Varianten unserer Methode verglichen, die als OURS(O/M) bzw. /Q bezeichnet werden /QM) lauten die Details wie folgt:
O: Keine Kartenwartung, keine IntrospektionsabfrageM: Nur Kartenwartung
Q: Nur IntrospektionsabfrageWir verwenden VGG-19 [^simonyan2014very^] als Hintergrund-Feature-Extraktor und verwenden eine lineare Ebene, um die extrahierten Features auf eine niedrigere Einbettungsdimension d=128 zu projizieren. Wir haben alle Basislinien für 10 Epochen in
Oxford Radar RobotCarmit einer Lernrate von 1e{-5} und einer Batchgröße von 8 trainiert.
Um die Leistung der Ortserkennung zu bewerten, verwenden wir Recall@N (R@N)Recall@N (R@N) 指标，这是通过确定在 N 个候选者中是否至少有一个候选者接近 GPS/INS 所指示的地面真实值来确定的本地化的准确性。这对于自动驾驶应用中的安全保证尤为重要，因为它反映了系统对假阴性率的校准。我们还使用 Average Precision (AP) 来测量所有召回级别的平均精度。最后，我们使用 F-scores 与 beta=2/1/0.5 来分配召回对精确度的重要性级别，作为评估整体识别性能的综合指标。
此外，为了评估不确定性估计性能。我们使用 Recall@RR，在这里我们执行内省查询拒绝，并在不同的不确定性阈值级别上评估 Recall@N=1 -- 拒绝所有查询的扫描的不确定性大于阈值的。我们因此拒绝了 0-100% 的查询。
如 Oxford Radar RobotCar实验中表格1所示，我们的方法仅使用度量学习模块，在所有指标上都取得了最高的性能。具体来说，在 Recall@1 方面，我们的方法 OURS(O) 展示了通过变分对比学习框架学习的方差解耦表示的有效性，实现了超过 90.46% 的识别性能。这进一步得到了 MulRan 实验结果的支持，如表2所示，我们的方法在 Recall@1、总体 F-scores 和 AP 上均优于其他所有方法。尽管在 MulRan 实验中，VAE 在 Recall@5/10 上优于我们的方法，但我们的方法在两种设置中的最佳 F-1/0.5/2 和 AP Indikator, der bestimmt, ob es mindestens einen Kandidaten unter N Kandidaten gibt Die Lokalisierung wird durch Annäherung an die durch GPS/INS angezeigte Grundwahrheit bestimmt. Dies ist besonders wichtig für die Sicherheit bei autonomen Fahranwendungen, da es die Systemkalibrierung der Falsch-Negativ-Rate widerspiegelt. Wir verwenden auch
Average Precision (AP)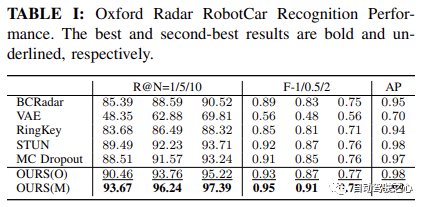 
um die durchschnittliche Präzision aller Rückrufstufen zu messen. Schließlich verwenden wir
F-scores und
beta=2/1/0.5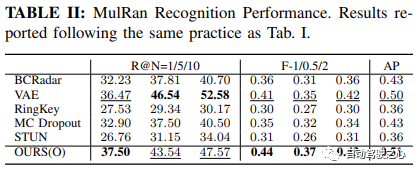
Recall@RR, wo wir eine introspektive Abfrageablehnung durchführen und bei verschiedenen Unsicherheitsschwellenwerten auswerten 🎜 🎜Recall@N=1🎜 🎜-- Ablehnen Alle Abfragen werden mit größerer Unsicherheit gescannt als der Schwellenwert. Wir lehnen daher 0-100 % der Anfragen ab. 🎜Recall@1🎜 🎜In Bezug auf die Leistung demonstriert unsere Methode OURS(O) die Wirksamkeit der varianzentkoppelten Darstellung, die durch ein Variations-Kontrast-Lern-Framework erlernt wurde, und erreicht eine Erkennungsleistung von mehr als 90,46 %. Dies wird durch die experimentellen Ergebnisse von 🎜 🎜MulRan🎜 weiter gestützt. Wie in Tabelle 2 gezeigt, hat unsere Methode einen besseren 🎜 -radius: 4px; overflow-wrap: break-word; text-indent: 0px; ;">Recall@1, insgesamt 🎜 🎜F-scores🎜 🎜 und 🎜 🎜Recall@5/10 🎜 🎜 übertrifft unsere Methode, aber unsere Methode ist die beste der beiden Einstellungen 🎜 🎜Recall@1Recall@1 进一步提高到 93.67%，超过了当前最先进的方法 STUN，超出了 4.18%。这进一步证明了学习方差作为一个有效的不确定性度量，以及基于不确定性的地图集成策略在提高地点识别性能方面的有效性。
随着被拒绝的不确定查询的百分比增加，识别性能的变化，特别是 Recall@1，在 Oxford Radar RobotCar 实验中如图1所示，在 MulRan 实验中如图2所示。值得注意的是，我们的方法是唯一一个在两种实验设置中都展示出随着不确定查询拒绝率增加而持续改进的识别性能的方法。在MulRan实验中，OURS(Q) 是唯一一个随着拒绝率增加而持续平稳地提高 Recall@RR 指标的方法。与 VAE 和 STUN 相比，这两种方法也像我们的方法一样估计了模型的不确定性，OURS(Q) 在 Recall@RR=0.1/0.2/0.5 上实现了 +(1.32/3.02/8.46)% 的改进，而 VAE 和 STUN 分别下降了 -(3.79/5.24/8.80)% 和 -(2.97/4.16/6.30)%。
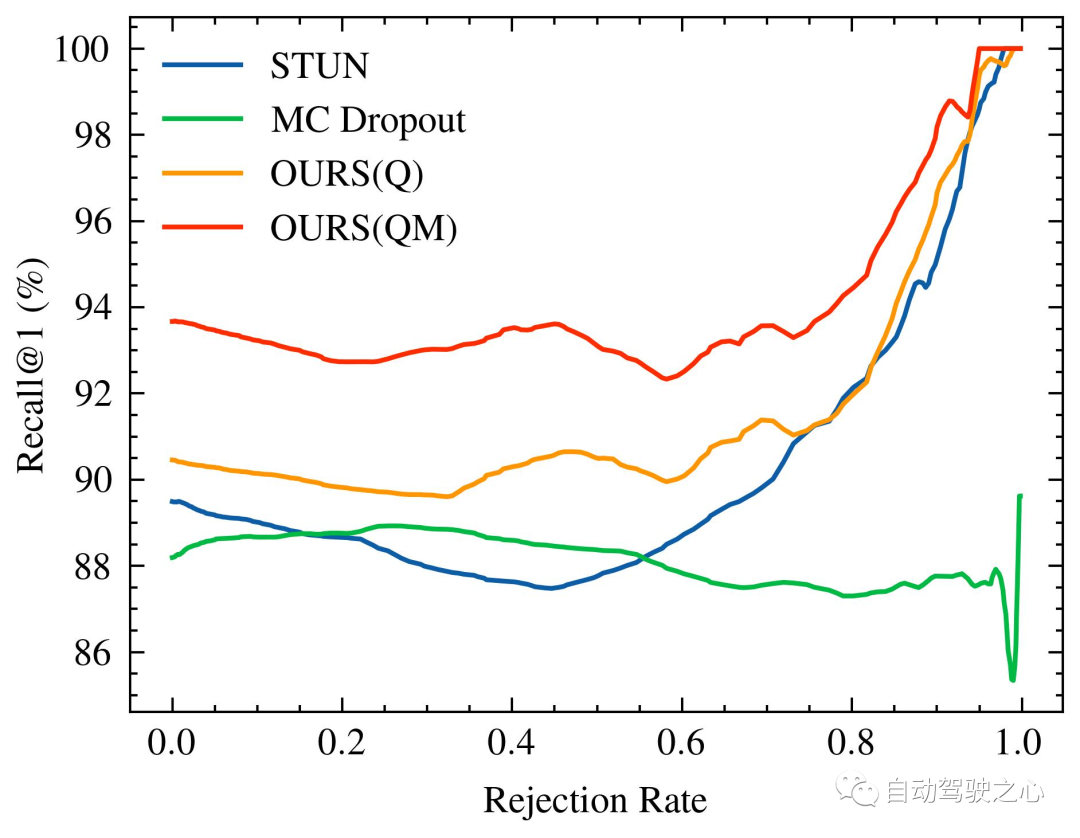
Oxford Radar RobotCar的内省查询拒绝性能。随着被拒绝的不确定查询的百分比增加，Recall@1增加/减少。由于 VAE 的性能与其他方法相比较低（具体为Recall@RR=0.1/0.2/0.5的 (48.42/48.08/18.48)%），因此没有进行可视化。
Mulran的内省查询拒绝性能。格式同上。
另一方面，与 MC Dropout 相比，后者估计了由于数据偏见和模型误差导致的认知不确定性，尽管它在Oxford Radar RobotCar实验的早期阶段有更高的 Recall@1 增加，但其性能总体上低于我们的，并且随着拒绝率进一步增加，未能实现更大的改进。最后，比较 OURS(Q) 和 OURS(QM) 在Oxford Radar RobotCar实验中，我们观察到 Recall@RR weiter verbessert auf 93,67 %, übertrifft die aktuelle State-of-the-Art-Methode STUN um 4,18 %. Dies zeigt weiter die Wirksamkeit der erlernten Varianz als wirksames Unsicherheitsmaß und der auf Unsicherheit basierenden Kartenintegrationsstrategie bei der Verbesserung der Ortserkennungsleistung.
Recall@1, in Experiment Wie in Abbildung 1 gezeigt das
MulRan
Recall@RR🎜 🎜 Indikatormethode. Im Vergleich zu VAE und STUN, die wie unsere Methode auch die Modellunsicherheit schätzen, ist OURS(Q) in 🎜 🎜Recall@RR=0.1/0.2/0.5🎜 🎜implementiert am Es gab eine Verbesserung von +(1.32/ 3,02/8,46) %, während VAE und STUN um -(3,79/5,24/8,80) % bzw. -(2,97/4,16/6,30) % sanken. 🎜🎜🎜🎜 Leistung bei der Ablehnung von Introspektionsabfragen von Oxford Radar RobotCar. Da der Prozentsatz abgelehnter unbestimmter Abfragen zunimmt, Recall@1erhöhen/verringern. Aufgrund der geringen Leistung von VAE im Vergleich zu anderen Methoden (insbesondere Recall@RR=0.1/0.2/0.5's (48.42/48.08/18.48)%), daher wird es nicht visualisiert. 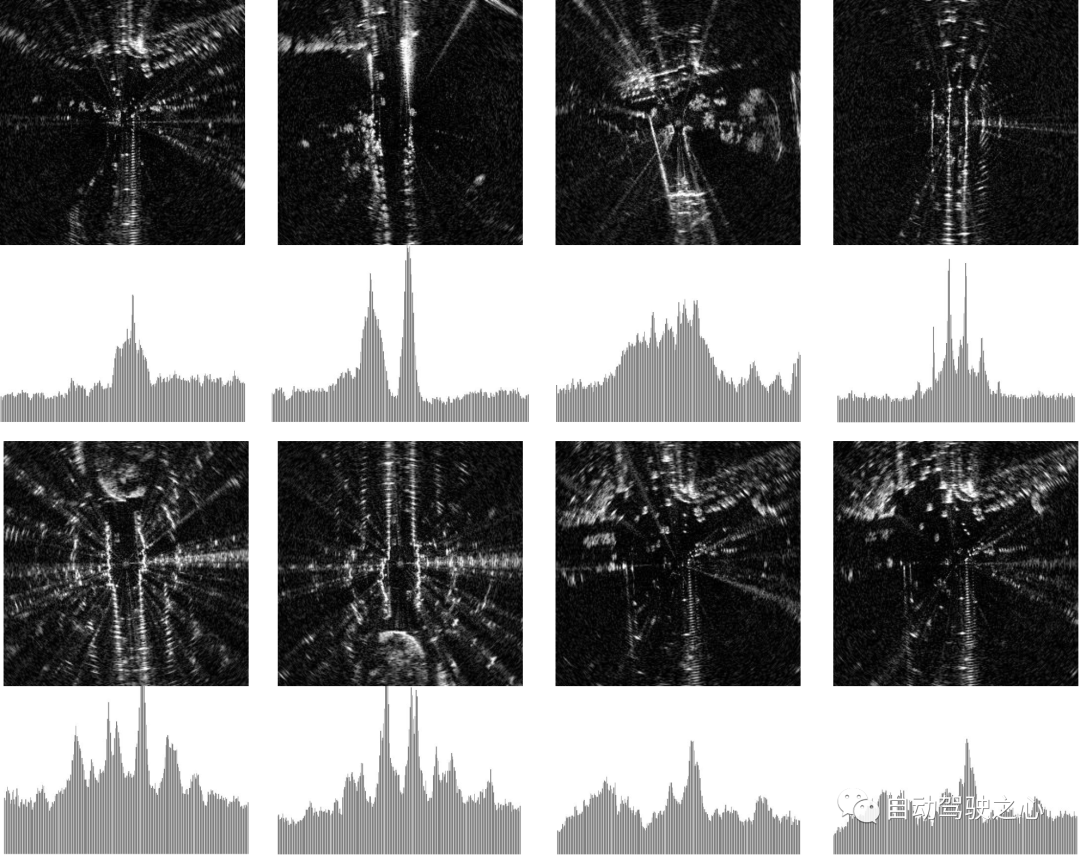🎜🎜🎜🎜 Mulrans introspektive Abfrageablehnungsleistung. Das Format ist das gleiche wie oben. 🎜🎜Andererseits im Vergleich zu MC Dropout, das die epistemische Unsicherheit aufgrund von Datenverzerrungen und Modellfehlern schätzt, obwohl es in den frühen Phasen des Oxford Radar RobotCar-Experiments einen höheren 🎜 aufwies 🎜Recall@1 🎜 🎜 steigerte sich, aber seine Leistung war im Allgemeinen geringer als unsere und es konnten keine größeren Verbesserungen erzielt werden, da die Ablehnungsrate weiter zunahm. Schließlich haben wir beim Vergleich von OURS(Q) und OURS(QM) im Oxford Radar RobotCar-Experiment Folgendes beobachtet: 4px; overflow-wrap: break-word; text-indent: 0px; display: inline-block;">Recall@RR🎜 🎜 hat ähnliche Änderungsmuster, aber es gibt eine beträchtliche Lücke zwischen ihnen. Dies legt nahe, dass introspektive Abfrage- und Kartenwartungsmechanismen unabhängig voneinander zum Ortserkennungssystem beitragen, wobei jeder Mechanismus Unsicherheitsmaße auf integrale Weise nutzt. 🎜🎜🎜 Diskussion zu „Off the Radar“ 🎜🎜🎜🎜 Qualitative Analyse und Visualisierung 🎜🎜🎜 Zur qualitativen Bewertung von Unsicherheitsquellen in der Radarwahrnehmung stellen wir mithilfe unserer Methode „Visueller Vergleich von Unsicherheitsstichproben“ hohe/niedrige Schätzungen in zwei Datensätzen bereit. Wie gezeigt, zeigen Radarscans mit hoher Unsicherheit typischerweise starke Bewegungsunschärfe und spärliche unentdeckte Bereiche, während Scans mit niedriger Unsicherheit typischerweise deutliche Merkmale mit stärkerer Intensität im Histogramm enthalten. 🎜🎜🎜🎜Visualisierung von Radarscans mit unterschiedlichen Unsicherheitsgraden. Die vier Beispiele auf der linken Seite stammen aus dem Oxford Radar RobotCar Dataset, während die vier Beispiele auf der rechten Seite aus MulRan stammen. Wir zeigen die Top-10-Proben mit der höchsten (oben) bzw. niedrigsten (unten) Unsicherheit. Radarscans werden zur Verbesserung des Kontrasts in kartesischen Koordinaten angezeigt. Das Histogramm unter jedem Bild zeigt die RingKey-Deskriptormerkmale der aus allen Azimutwinkeln extrahierten Intensität.
Dies stützt unsere Hypothese über die Quelle der Unsicherheit in der Radarwahrnehmung weiter und dient als qualitativer Beweis dafür, dass unsere Unsicherheitsmessungen dieses Datenrauschen erfassen.
In unseren Benchmark-Experimenten haben wir erhebliche Unterschiede in der Erkennungsleistung zwischen den beiden Datensätzen beobachtet. Wir glauben, dass die Größe der verfügbaren Trainingsdaten ein legitimer Grund sein könnte. Der Trainingssatz von Oxford Radar RobotCar umfasst mehr als 300 km Fahrerfahrung, während der MulRan-Datensatz nur etwa 120 km umfasst. Berücksichtigen Sie jedoch auch die Leistungseinbußen der RingKey-Deskriptormethode. Dies deutet darauf hin, dass es bei der Radarszenenwahrnehmung inhärente, nicht unterscheidbare Merkmale geben könnte. Wir haben beispielsweise festgestellt, dass Umgebungen mit wenigen offenen Bereichen häufig zu identischen Scans und einer suboptimalen Erkennungsleistung führten. Wir zeigen anhand dieses Datensatzes, was in diesen Situationen mit hoher Unsicherheit mit unserem System und verschiedenen Basislinien passiert.
Originallink: https://mp.weixin.qq.com/s/wu7whicFEAuo65kYp4quow
Das obige ist der detaillierte Inhalt vonSo implementieren Sie die FMCW-Radarpositionserkennung elegant (IROS2023). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Aktivierungscode für den Vista-Schlüssel
Welche Methoden gibt es, um die IP in dynamischen VPS sofort zu ändern?
So lösen Sie das Problem, dass diese Windows-Kopie nicht echt ist
Was soll ich tun, wenn mein QQ-Konto gestohlen wird?
Was ist der Unterschied zwischen dem TCP-Protokoll und dem UDP-Protokoll?
So beheben Sie den Fehler 0xc000409
So lösen Sie das Problem, dass document.cookie nicht abgerufen werden kann
Was beinhalten Computersoftwaresysteme?
![[Web-Frontend] Node.js-Schnellstart](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
