Ein Zahlenspiel?-C++-php.cn

Number Connect ist ein Logikrätsel, bei dem es darum geht, Wege zu finden, die Zahlen in einem Raster verbinden.

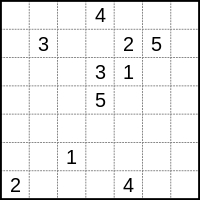
Ein Zahlenspiel?

Ein einfaches Beispiel für ein Numberlink-Rätsel. Lösung für ein Numberlink-Rätsel.

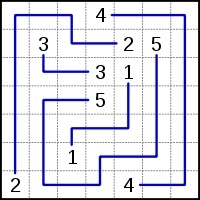
Ein Zahlenspiel?

Regeln: Die Spieler müssen alle übereinstimmenden Zahlen im Raster mit einer einzigen durchgehenden Linie (oder einem Pfad) zuordnen. Linien dürfen nicht auseinanderlaufen oder sich kreuzen, und die Zahlen müssen am Ende jeder Linie stehen (d. h. nicht in der Mitte). Ein Problem gilt nur dann als gut gestaltet, wenn es eine eindeutige Lösung hat und alle Zellen im Raster gefüllt sind, obwohl einige Numberlink-Designer dies nicht vorschreiben.

Spiel – Betrachten Sie eine n×n-Reihe von Quadraten. Einige der Quadrate sind leer, andere sind ausgefüllt und einige nicht ausgefüllte Quadrate sind durch die ganzen Zahlen 1, 2, 3, ... gekennzeichnet. Jede ganze Zahl belegt zwei verschiedene Felder auf der Tafel. Die Aufgabe des Spielers besteht darin, die beiden Vorkommen jeder Ganzzahl auf dem Spielbrett über einen einfachen Pfad zu verbinden, indem er nur horizontale und vertikale Bewegungen verwendet. Es ist nicht erlaubt, dass sich zwei unterschiedliche Wege kreuzen. Kein Pfad darf feste Blöcke enthalten (auf keinem Pfad sind feste Blöcke zulässig). Schließlich müssen alle nicht durchgezogenen Quadrate durch Pfade gefüllt werden.

Algorithmus – Um ein effizientes Zufallsrätsel bei einer Brettgröße n×n vorzubereiten, generieren wir zunächst zufällige einfache disjunkte Pfade auf dem Brett. Wenn es mehrere isolierte Blöcke gibt, die außerhalb aller generierten Pfade verbleiben, markieren Sie diese isolierten Blöcke als fest (verboten). Als Puzzle verwenden wir dann die Endpunkte des Pfades und die Liste der ausgefüllten Quadrate.

Also generieren wir zunächst eine Lösung und lösen dann aus der Lösung das Rätsel. Pfade und ausgefüllte Quadrate unterteilen das n×n-Schachbrett in Teile. Wir verwenden die Union-Lookup-Datenstruktur, um diese Aufteilung zu generieren. Die Datenstruktur verarbeitet eine Teilmenge von n^2 Feldern auf dem Schachbrett.

Erklärung

Finden Sie zufällig Quadrate (i, j) und (k, l) auf dem Schachbrett, so dass: (a) (i, j) und (k, l) einander benachbart sind und (b ) Weder (i, j) noch (k, l) gehören zu einem der bisher generierten Pfade. Wenn auf der gesamten Tafel kein solches Quadratpaar gefunden wird, wird ein Fehler zurückgegeben /* Dabei sind (i, j) und (k, l) die ersten beiden Quadrate des neu zu konstruierenden Pfades. *
Füge zwei Union-Find-Bäume zusammen, die (i, j) und (k, l) enthalten.
Wiederholen Sie die folgenden Schritte, bis der aktuelle Pfad nicht mehr erweitert werden kann: Benennen Sie (i, j) in (k, l) um. Finden Sie zufällig die Nachbarquadrate (k, l) von (i, j), sodass: (a) (k, l) zu keinem bisher generierten Pfad gehört (einschließlich des aktuellen Pfads) (b) Auf dem aktuell konstruierten Pfad teilweise ( Der einzige Nachbar von i, j) ist (k, l).
Wenn kein solches Nachbarquadrat (k, l) gefunden wird, kann der Pfad nicht weiter verlängert werden, sodass die Schleife unterbrochen wird
Andernfalls ist die Vereinigung der beiden, die (i, j) und (k) enthält , l) wird der Suchsatzbaum zusammengeführt.
Setzen Sie die Flags der Start- und Endblöcke des neuen Pfads.
Rückgabe erfolgreich

Eingabe

| || || || || || || 4 |
| || || || || || 3 || |
| || || 2 || 2 || || || 3 |
| || || || || X || || 1 |
| || || 6 || || || 7 || 7 |
| 5 || 4 || || X || || X || 1 |
| || 5 || || 6 || || || |

Nach dem Login kopieren

Ausgabe

Lösung zur obigen Tabelle

| 4 || 4 || 4 || 4 || 4 || 4 || 4 |
| 4 || 1 || 1 || 1 || 1 || 3 || 3 |
| 4 || 1 || 2 || 2 || 1 || 1 || 3 |
| 4 || 1 || 1 || 1 || X || 1 || 1 |
| 4 || 4 || 6 || 1 || 1 || 7 || 7 |
| 5 || 4 || 6 || X || 1 || X || 1 |
| 5 || 5 || 6 || 6 || 1 || 1 || 1 |

Nach dem Login kopieren

Beispiel

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
   struct _node *parent;
   int rank;
   int path_number;
   int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
   int i, j;
   for (i=0;i<n;i++){
      for (j=0;j<n;j++){
         node *np;
         np = (node *)malloc(sizeof(node));
         np->rank = 0;
         np->parent = NULL;
         np->path_number = 0;
         np->endpoint = 0;
         arr[i][j] = np;
      }
   }
}
/*

Nach dem Login kopieren

Input:a node
Output:the set pointer of the set the node belongs to

Nach dem Login kopieren

Beschreibung – Ruft einen Knoten ab und gibt einen Set-Zeiger zurück . */

node *findset(node *n) {
   if (n->parent != NULL)
      n = n->parent;
   return n;
}
void setunion(node *x, node *y) {
   x = findset(x);
   y = findset(y);
   if (x->rank > y->rank)
      y->parent = x;
   else {
      x->parent = y;
      if(x->rank == y->rank)
         y->rank++;
   }
}
int neighbour(int n, node ***arr) {
   int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
   int k = rand()%(n*n);
   while (ct < (n*n)) {
      k %= (n*n);
      i1 = k/n;
      j1 = k%n;
      if (arr[i1][j1]->path_number==0) {
         int kk = rand()%4;
         int cc = 0;
         switch (kk) {
            case 0: i2= i1-1;
               j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 1: i2= i1-0;
               j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 2: i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 3: i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 4: if(cc==4)
               break;
            i2= i1-1;
            j2= j1-0;
            if(i2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 5: if(cc==4)
               break;
            i2= i1-0;
            j2= j1-1;
            if(j2>=0 && i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 6: if(cc==4)
               break;
            i2= i1+1;
            j2= j1-0;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
            case 7: if(cc==4)
               break;
            i2= i1-0;
            j2= j1+1;
            if(i2<n && j2<n) {
               if(arr[i2][j2]->path_number==0) {
                  flag=1;
                  break;
               }
            }
            cc++;
         }
      }
      if(flag==1)
         break;
         ct++;
         k++;
   }
   if(ct<n*n) {
      k2= (i2*n)+j2;
      return k*(n*n)+k2;
   } else {
      return -1;
   }
}
int checkneigh(int k1, int k2, int n, node ***arr) {
   int i= k2/n;
   int j= k2%n;
   int ii= k1/n;
   int jj= k1%n;
   int ct=0;
   if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
      ct++;
   if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
      ct++;
   if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
      ct++;
   if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
      ct++;
   if(ct>1)
      return 0;
   else
      return 1;
}
int valid_next(int k, int n, node ***arr) {
   int i1, i2, j1, j2, a, b, kk, stat,ct=0;
   int flag=0;
   i1= k/n;
   j1= k%n;
   kk= rand()%4;
   switch(kk) {
      case 0: i2= i1-1;
         j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 1: i2= i1-0;
         j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 2: i2= i1+1;
         j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 3: i2= i1-0;
         j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 4: if(ct==4)
         break;
      i2= i1-1;
      j2= j1-0;
      if(i2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 5: if(ct==4)
         break;
      i2= i1-0;
      j2= j1-1;
      if(j2>=0 && i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 6: if(ct==4)
         break;
      i2= i1+1;
      j2= j1-0;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
      case 7: if(ct==4)
         break;
      i2= i1-0;
      j2= j1+1;
      if(i2<n && j2<n) {
         if(arr[i2][j2]->path_number==0) {
            stat= checkneigh(k, (n*i2 + j2),n,arr);
            //printf("%d</p><p>",stat);
            if(stat) {
               flag=1;
               break;
            }
         }
      }
      ct++;
   }
   //printf("flag- %d</p><p>",flag);
   if(flag==0)
      return -1;
   if(flag) {
      //printf("value sent- %d</p><p>", i2*n + j2);
      return (i2*n)+j2;
   }
}
int addpath(node ***arr, int n, int ptno) {
   int a,b,k1,k2;
   int i1,j1,i2,j2;
   k2= neighbour( n, arr);
   if(k2==-1) //no valid pair found to start with
      return 0;
   k1= k2/(n*n);
   k2= k2%(n*n);
   //printf("%d %d</p><p>",k1,k2);
   i1= k1/n;
   j1= k1%n;
   i2= k2/n;
   j2= k2%n;
   arr[i1][j1]->endpoint= 1;
   arr[i2][j2]->path_number= ptno;
   arr[i1][j1]->path_number= ptno;
   node *n1, *n2;
   n1= arr[i1][j1];
   n2= arr[i2][j2];
   n1= findset(n1);
   n2= findset(n2);
   setunion(n1, n2);
   while(1) {
      i1= i2;
      j1= j2;
      k1= (i1*n)+j1;
      k2= valid_next(k1,n,arr);
      if(k2==-1) {
         arr[i1][j1]->endpoint= 1;
         break;
      }
      i2=k2/n;
      j2=k2%n;
      arr[i2][j2]->path_number= ptno;
      node *n1, *n2;
      n1= arr[i1][j1];
      n2= arr[i2][j2];
      n1= findset(n1);
      n2= findset(n2);
      setunion(n1,n2);
   }
   return 1;
}
void printtable(node ***arr, int n) {
   int i,j;
   printf("Table to be solved:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->endpoint ==1){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else if(arr[i][j]->path_number==0)
            printf("| X |");
         else
            printf("| |");
      }
      printf("</p><p>");
   }
   printf("</p><p></p><p>The solution to the above table:</p><p>");
   for(i=0;i<n;i++) {
      for(j=0;j<n;j++) {
         if(arr[i][j]->path_number != 0){
            if(arr[i][j]->path_number/10==0)
               printf("| %d |",arr[i][j]->path_number);
            else
               printf("| %d|",arr[i][j]->path_number);
         } else
            printf("| X |");
      }
      printf("</p><p>");
   }
}
int main(void) {
   srand((unsigned int) time (NULL));
   int i, j;
   int ct = 1;
   int n = 7;
   node*** pointers= (node ***)malloc(n*sizeof(node **));
   for (i=0; i<n; i++)
      pointers[i] = (node **)malloc(n*sizeof(node *));
   initboard(pointers, n);
   while(1) {
      i = addpath(pointers, n, ct);
      if (i==0) {
         break;
      } else {
         ct++;
      }
   }
   printtable(pointers,n);
   return 0;
}

Nach dem Login kopieren

Das obige ist der detaillierte Inhalt vonEin Zahlenspiel?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!