
Hier sehen wir die Fläche des größten Lucas-Dreiecks eines Quadrats, das in einen Halbkreis eingeschrieben ist. Angenommen, der Radius des Halbkreises sei R, die Seitenlänge des Quadrats sei „a“ und die Höhe des Lucas-Dreiecks sei h.
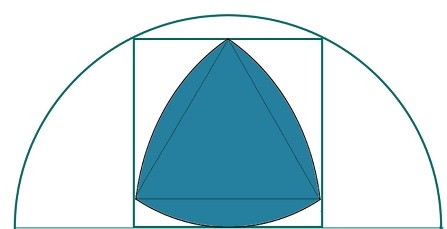
Wir wissen, dass die Seitenlänge eines in einen Halbkreis eingeschriebenen Quadrats -
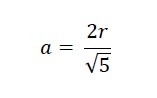
beträgt. Die Höhe des Lucas-Dreiecks ist gleich der Seitenlänge. Also a = h. Daher beträgt die Fläche des Lucas-Dreiecks -
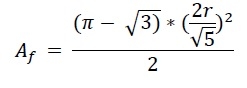
#include <iostream>
#include <cmath>
using namespace std;
float areaReuleaux(float r) { //radius of the semicircle is r
if (r < 0) //if r is negative it is invalid
return -1;
float area = ((3.1415 - sqrt(3)) * (2*r/(sqrt(5))) * (2*r/(sqrt(5))))/2;
return area;
}
int main() {
float rad = 8;
cout << "Area of Reuleaux Triangle: " << areaReuleaux(rad);
}Area of Reuleaux Triangle: 36.0819
Das obige ist der detaillierte Inhalt vonWas ist das größte Luula-Kurvendreieck, das in ein Quadrat innerhalb eines Halbkreises eingeschrieben ist?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Verwendung der fscanf-Funktion
Verwendung der fscanf-Funktion
 So öffnen Sie eine MDS-Datei
So öffnen Sie eine MDS-Datei
 So lösen Sie das Problem, dass Ethernet keine Verbindung zum Internet herstellen kann
So lösen Sie das Problem, dass Ethernet keine Verbindung zum Internet herstellen kann
 So verwenden Sie die Max-Funktion
So verwenden Sie die Max-Funktion
 So öffnen Sie die Hosts-Datei
So öffnen Sie die Hosts-Datei
 Was tun, wenn der Computer den Tod vortäuscht?
Was tun, wenn der Computer den Tod vortäuscht?
 Verwendung der Funktion createmutex
Verwendung der Funktion createmutex
 Erstellen Sie einen Internetserver
Erstellen Sie einen Internetserver




