Wir wissen, dass die Quantisierung von Aktivierungen, Gewichten und Gradienten in 4-Bit für die Beschleunigung des Trainings neuronaler Netze sehr wertvoll ist. Bestehende 4-Bit-Trainingsmethoden erfordern jedoch benutzerdefinierte Zahlenformate, die von moderner Hardware nicht unterstützt werden. In diesem Artikel schlagen Tsinghua Zhu Jun et al. eine Transformer-Trainingsmethode vor, die den INT4-Algorithmus verwendet, um alle Matrixmultiplikationen zu implementieren.
Ob das Modell schnell trainiert wird oder nicht, hängt eng mit den Anforderungen an Aktivierungswerte, Gewichte, Steigungen und andere Faktoren zusammen.
Das Training neuronaler Netze erfordert einen gewissen Rechenaufwand, und die Verwendung von Algorithmen mit geringer Präzision (Vollquantisierungstraining oder FQT-Training) soll die Rechen- und Speichereffizienz verbessern. FQT fügt dem ursprünglichen Berechnungsgraphen mit voller Präzision Quantisierer und Dequantisierer hinzu und ersetzt teure Gleitkommaoperationen durch billige Gleitkommaoperationen mit geringer Genauigkeit.
Die Forschung zu FQT zielt darauf ab, die numerische Genauigkeit des Trainings zu reduzieren und gleichzeitig die Einbußen bei Konvergenzgeschwindigkeit und -genauigkeit zu verringern. Die erforderliche numerische Genauigkeit wird von FP16 auf FP8, INT32+INT8 und INT8+INT5 reduziert. Das FP8-Training wird auf Nvidia H100-GPUs mit der Transformer-Engine durchgeführt, was eine erstaunliche Beschleunigung umfangreicher Transformer-Trainings ermöglicht.
Vor Kurzem wurde die numerische Genauigkeit des Trainings auf 4 Bit reduziert. Sun et al. haben mehrere moderne Netzwerke mit INT4-Aktivierungen/-Gewichten und FP4-Gradienten erfolgreich trainiert. Chmiel et al. haben ein benutzerdefiniertes 4-stelliges logarithmisches Zahlenformat vorgeschlagen. Diese 4-Bit-Trainingsmethoden können jedoch nicht direkt zur Beschleunigung verwendet werden, da sie benutzerdefinierte Zahlenformate erfordern, die auf aktueller Hardware nicht unterstützt werden.
Beim Training auf einem so niedrigen Niveau wie 4 Bit gibt es enorme Optimierungsherausforderungen. Erstens führt der nicht differenzierbare Quantisierer der Vorwärtsausbreitung dazu, dass der Verlustfunktionsgraph ungleichmäßig wird, und der auf Gradienten basierende Optimierer kann leicht stecken bleiben lokales Minimum ausgezeichnet. Zweitens kann der Gradient nur mit geringer Genauigkeit berechnet werden. Dieser ungenaue Gradient verlangsamt den Trainingsprozess und führt sogar zu einem instabilen oder divergenten Training.
Dieser Artikel schlägt einen neuen INT4-Trainingsalgorithmus für das beliebte neuronale Netzwerk Transformer vor. Die teuren linearen Operationen, die zum Trainieren von Transformatoren verwendet werden, können alle in Form einer Matrixmultiplikation (MM) geschrieben werden. Der MM-Formalismus ermöglicht es Forschern, flexiblere Quantisierer zu entwerfen. Dieser Quantisierer nähert sich der FP32-Matrixmultiplikation durch spezifische Aktivierungs-, Gewichts- und Gradientenstrukturen in Transformer besser an. Der Quantisierer in diesem Artikel nutzt auch neue Fortschritte in der stochastischen numerischen linearen Algebra.
Bilder
Papieradresse: https://arxiv.org/pdf/2306.11987.pdf
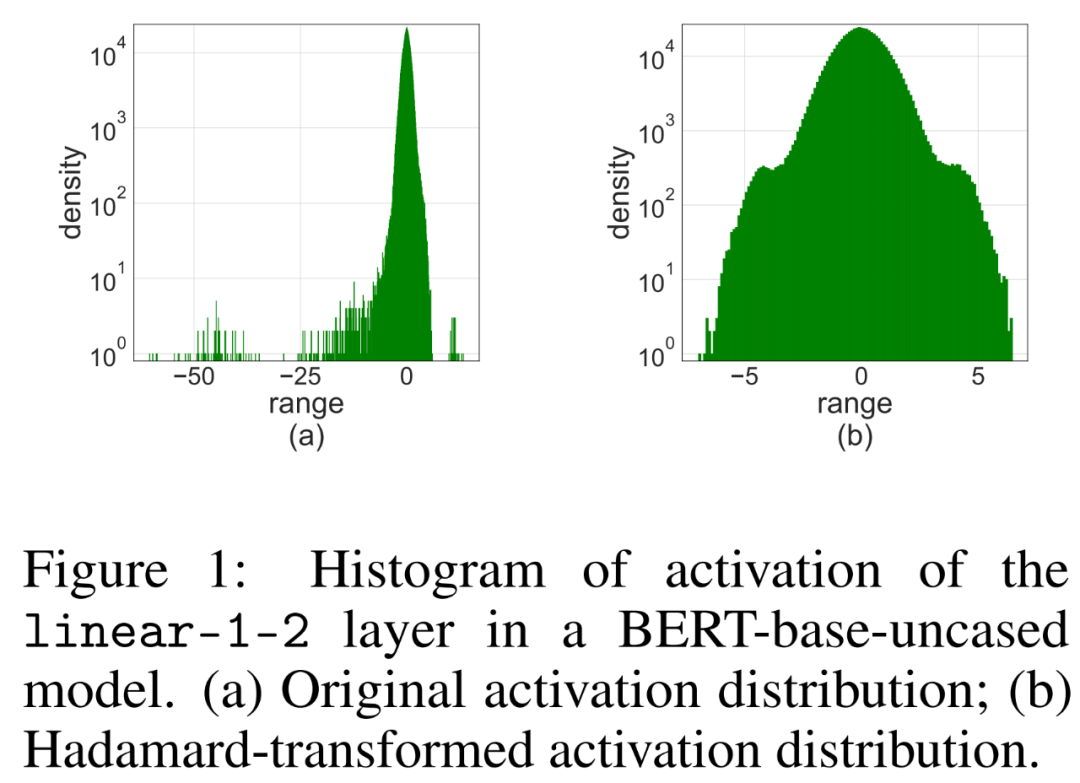
Untersuchungen zeigen, dass bei der Vorwärtsausbreitung der Hauptgrund für die Abnahme der Genauigkeit Anomalien im Aktivierungswert sind . Um diesen Ausreißer zu unterdrücken, wird der Hadamard-Quantisierer vorgeschlagen, der zur Quantisierung der transformierten Aktivierungsmatrix verwendet wird. Bei dieser Transformation handelt es sich um eine blockdiagonale Hadamard-Matrix, die die von den Ausreißern übertragenen Informationen auf die Matrixeinträge in der Nähe der Ausreißer verteilt und dadurch den numerischen Bereich der Ausreißer einschränkt.
Für die Rückausbreitung nutzt die Studie die strukturelle Spärlichkeit des Aktivierungsgradienten. Untersuchungen zeigen, dass die Gradienten einiger Token sehr groß sind, aber gleichzeitig sind die Gradienten der meisten anderen Token sehr klein, und sogar die quantisierten Residuen größerer Gradienten sind kleiner. Anstatt diese kleinen Gradienten zu berechnen, werden daher die Rechenressourcen verwendet, um die Residuen größerer Gradienten zu berechnen.
Dieser Artikel kombiniert die Quantisierungstechniken der Vorwärts- und Rückwärtsausbreitung und schlägt einen Algorithmus vor, der INT4-MMs für alle linearen Operationen in Transformer verwendet. Die Studie evaluierte Algorithmen zum Trainieren von Transformern für eine Vielzahl von Aufgaben, darunter das Verstehen natürlicher Sprache, die Beantwortung von Fragen, maschinelle Übersetzung und Bildklassifizierung. Der vorgeschlagene Algorithmus erreicht eine vergleichbare oder bessere Genauigkeit im Vergleich zu bestehenden 4-Bit-Trainingsbemühungen. Darüber hinaus ist der Algorithmus mit moderner Hardware (z. B. GPUs) kompatibel, da keine benutzerdefinierten Zahlenformate (z. B. FP4 oder logarithmische Formate) erforderlich sind. Und der von der Forschung vorgeschlagene Prototyp-Quantisierungs- + INT4-MM-Operator ist 2,2-mal schneller als die FP16-MM-Basislinie und erhöht die Trainingsgeschwindigkeit um 35,1 %.
Während des Trainingsprozesses verwendeten die Forscher den INT4-Algorithmus, um alle linearen Operatoren zu beschleunigen und alle nichtlinearen Operatoren mit geringer Rechenintensität auf das FP16-Format einzustellen. Alle linearen Operatoren in Transformer können in Matrixmultiplikationsform geschrieben werden. Zu Demonstrationszwecken betrachteten sie eine einfache Beschleunigung der Matrixmultiplikation wie folgt.
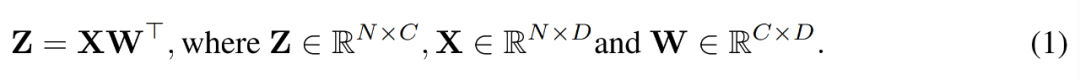Bild
Der Hauptanwendungsfall für diese Art der Matrixmultiplikation ist die vollständig verbundene Schicht.
Erlernte Schrittgrößenquantisierung
Beschleunigtes Training muss Ganzzahloperationen verwenden, um die Vorwärtsausbreitung zu berechnen. Daher nutzten die Forscher den erlernten Schrittgrößenquantisierer (LSQ). Als statische Quantisierungsmethode hängt die Quantisierungsskala von LSQ nicht von der Eingabe ab und ist daher kostengünstiger als dynamische Quantisierungsmethoden. Im Gegensatz dazu erfordern dynamische Quantisierungsmethoden die dynamische Berechnung der Quantisierungsskala bei jeder Iteration.
Gegeben eine FP-Matrix X, quantisiert LSQ X durch die folgende Formel (2) in eine ganze Zahl.
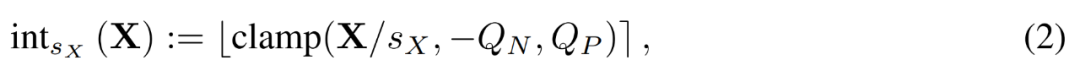Bilder
Ausreißer aktivieren
Die einfache Anwendung von LSQ auf FQT (vollständig quantisiertes Training, vollständig quantisiertes Training) mit 4-Bit-Aktivierung/Gewichtung führt zu einer Ausreißeraktivierung, da dies zu einer Verringerung von führt Genauigkeit. Wie in Abbildung 1 (a) unten dargestellt, werden einige Ausreißerterme aktiviert, deren Größe viel größer ist als bei anderen Termen.
In diesem Fall ist die Schrittgröße s_X ein Kompromiss zwischen der Quantisierungsgranularität und dem Bereich der darstellbaren Werte. Wenn s_X groß ist, können Ausreißer gut dargestellt werden, auf Kosten der groben Darstellung der meisten anderen Begriffe. Wenn s_X klein ist, müssen Terme außerhalb des Bereichs [−Q_Ns_X, Q_Ps_X] abgeschnitten werden.
Hadamard-Quantisierung
Forscher schlugen vor, den Hadamard-Quantisierer (HQ) zu verwenden, um das Ausreißerproblem zu lösen.
Ausreißer in der Aktivierungsmatrix können Strukturen auf Merkmalsebene bilden. Diese Ausreißer sind in der Regel entlang einiger Dimensionen geclustert, das heißt, nur wenige Spalten in X sind deutlich größer als die anderen. Als lineare Transformation kann die Hadamard-Transformation Ausreißer unter anderen Termen verteilen. Insbesondere ist die Hadamard-Transformation H_k eine 2^k × 2^k-Matrix.
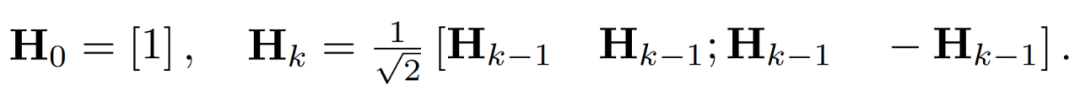
Um Ausreißer zu unterdrücken, quantisieren Forscher die transformierten Versionen von X und W.
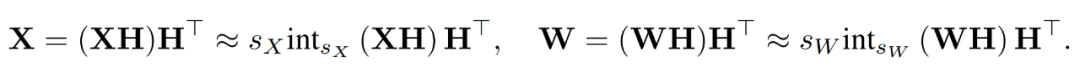
Durch die Kombination der quantisierten Matrizen erhielt der Forscher Folgendes.
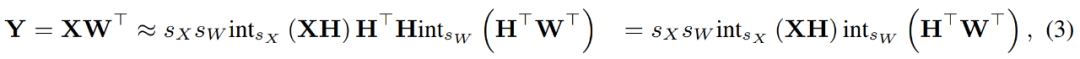
wobei sich die inversen Transformationen gegenseitig aufheben und MM wie folgt implementiert werden kann.
Bilder
Forscher nutzen INT4-Operationen, um die Backpropagation linearer Schichten zu beschleunigen. Der in Gleichung (3) definierte lineare Operator HQ-MM hat vier Eingaben, nämlich Aktivierung X, Gewicht W und Schritte s_X und s_W. Angesichts des Ausgabegradienten ∇_YL in Bezug auf die Verlustfunktion L müssen sie die Gradienten dieser vier Eingaben berechnen.
Strukturelle Sparsamkeit von Gradienten
Forscher stellten fest, dass die Gradientenmatrix ∇_Y während des Trainingsprozesses oft sehr spärlich ist. Die Sparsity-Struktur ist so, dass einige Zeilen (d. h. Token) von ∇_Y große Terme haben, während die meisten anderen Zeilen nahe an Nullvektoren liegen. Sie haben ein Histogramm der zeilenspezifischen Norm ∥(∇_Y)_i:∥ für alle Zeilen in Abbildung 2 unten erstellt.
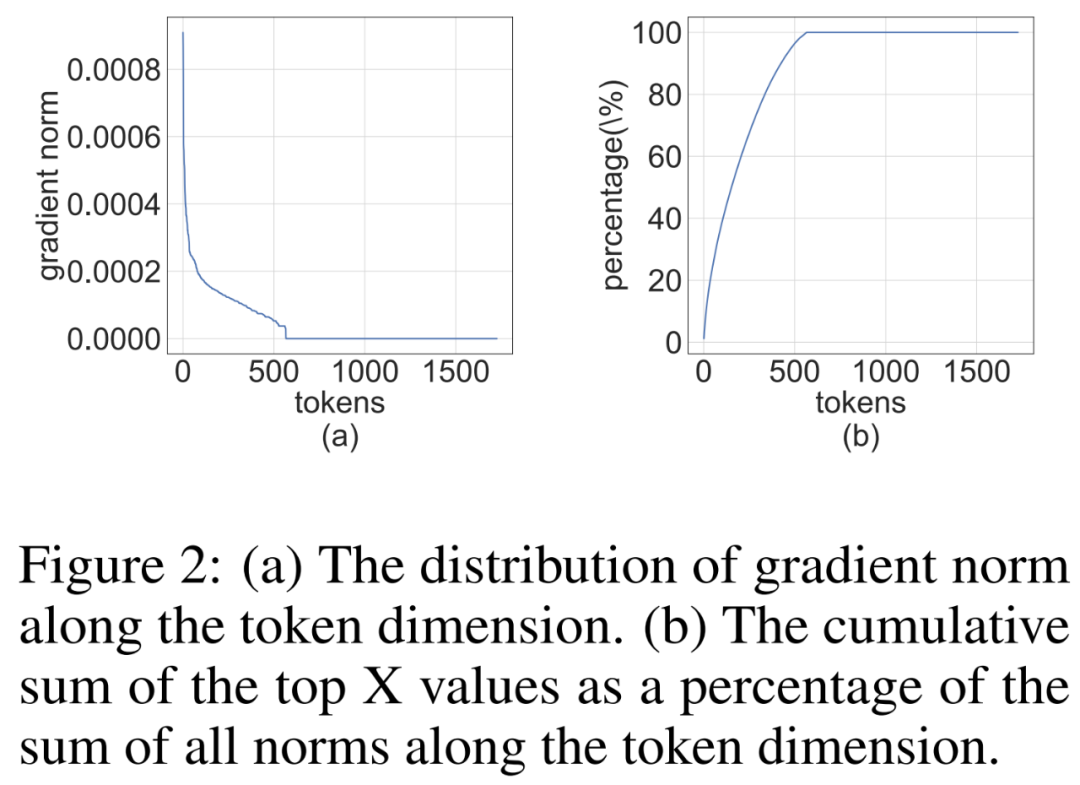Bilder
Bit-Split- und Average-Score-Sampling
Forscher diskutieren, wie man Gradientenquantisierer entwerfen kann, um die strukturelle Sparsität zu nutzen und MM während der Backpropagation genau zu berechnen. Die allgemeine Idee besteht darin, dass der Gradient vieler Zeilen sehr klein ist, sodass die Auswirkungen auf den Parametergradienten ebenfalls gering sind, aber viele Berechnungen verschwendet werden. Darüber hinaus können große Zeilen durch INT4 nicht genau dargestellt werden.
Um diese Sparsität auszunutzen, schlagen Forscher eine Bitaufteilung vor, die den Gradienten jedes Tokens in höhere 4 Bits und niedrigere 4 Bits aufteilt. Dann wird der Gradient mit den meisten Informationen durch Durchschnittspunktzahl-Stichprobe ausgewählt, was eine wichtige Stichprobentechnik von RandNLA ist.
Die Studie evaluierte den INT4-Trainingsalgorithmus für eine Vielzahl von Aufgaben, darunter die Feinabstimmung des Sprachmodells, maschinelle Übersetzung und Bildklassifizierung. Die Studie implementierte die vorgeschlagenen HQ-MM- und LSS-MM-Algorithmen mithilfe von CUDA und Cutlass2. Zusätzlich zur einfachen Verwendung von LSQ als Einbettungsschicht haben wir alle Gleitkomma-Linearoperatoren durch INT4 ersetzt und die volle Genauigkeit des Klassifikators der letzten Schicht beibehalten. Dabei übernahmen die Forscher Standardarchitekturen, Optimierer, Planer und Hyperparameter für alle bewerteten Modelle.
Konvergente Modellgenauigkeit. Tabelle 1 unten zeigt die Genauigkeit des konvergenten Modells für jede Aufgabe.
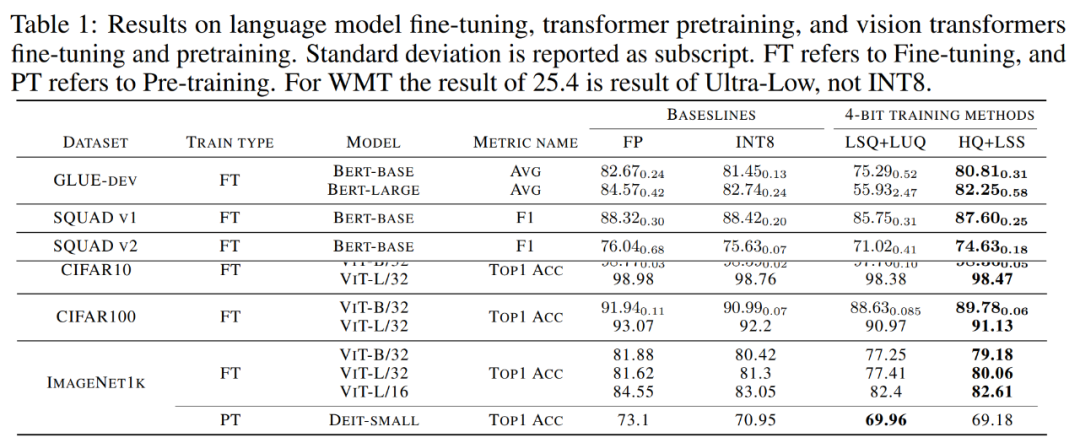Bilder
Feinabstimmung des Sprachmodells. Im Vergleich zu LSQ+LUQ verbessert der in der Studie vorgeschlagene Algorithmus die durchschnittliche Genauigkeit beim Bert-Basis-Modell um 5,5 % und beim Bert-Large-Modell um 25 %.
Das Forschungsteam demonstrierte außerdem weitere Ergebnisse des Algorithmus für SQUAD-, SQUAD 2.0-, Adversarial QA-, CoNLL-2003- und SWAG-Datensätze. Bei allen Aufgaben erzielt diese Methode eine bessere Leistung im Vergleich zu LSQ+LUQ. Im Vergleich zu LSQ+LUQ erreicht diese Methode Verbesserungen von 1,8 % bzw. 3,6 % bei SQUAD und SQUAD 2.0. Bei der schwierigeren kontradiktorischen Qualitätssicherung erreicht die Methode eine Verbesserung des F1-Scores um 6,8 %. Bei SWAG und CoNLL-2003 verbessert diese Methode die Genauigkeit um 6,7 % bzw. 4,2 %.
Maschinelle Übersetzung. Die Studie nutzte die vorgeschlagene Methode auch für das Vortraining. Diese Methode trainiert ein Transformer-basiertes [51] Modell für die maschinelle Übersetzung auf dem WMT 14 En-De-Datensatz. Die BLEU-Abbaurate von
HQ+LSS beträgt etwa 1,0 %, was kleiner ist als die 2,1 % von Ultra-low und höher als die im LUQ-Papier angegebenen 0,3 %. Dennoch ist die Leistung von HQ+LSS bei dieser Pre-Training-Aufgabe immer noch vergleichbar mit bestehenden Methoden und es unterstützt moderne Hardware.
Bildklassifizierung. Studie zum Laden vorab trainierter ViT-Kontrollpunkte auf ImageNet21k und deren Feinabstimmung auf CIFAR-10, CIFAR-100 und ImageNet1k.
Im Vergleich zu LSQ+LUQ verbessert die Forschungsmethode die Genauigkeit von ViT-B/32 und ViT-L/32 um 1,1 % bzw. 0,2 %. Auf ImageNet1k verbessert diese Methode die Genauigkeit um 2 % bei ViT-B/32, 2,6 % bei ViT-L/32 und 0,2 % bei ViT-L/32 im Vergleich zu LSQ+LUQ.
Das Forschungsteam testete die Wirksamkeit des Algorithmus weiter am vorab trainierten DeiT-Small-Modell auf ImageNet1K, wo HQ+LSS im Vergleich zu LSQ+LUQ immer noch auf ein ähnliches Maß an Genauigkeit konvergieren kann und gleichzeitig hardwarefreundlicher ist .
Ablationsstudie
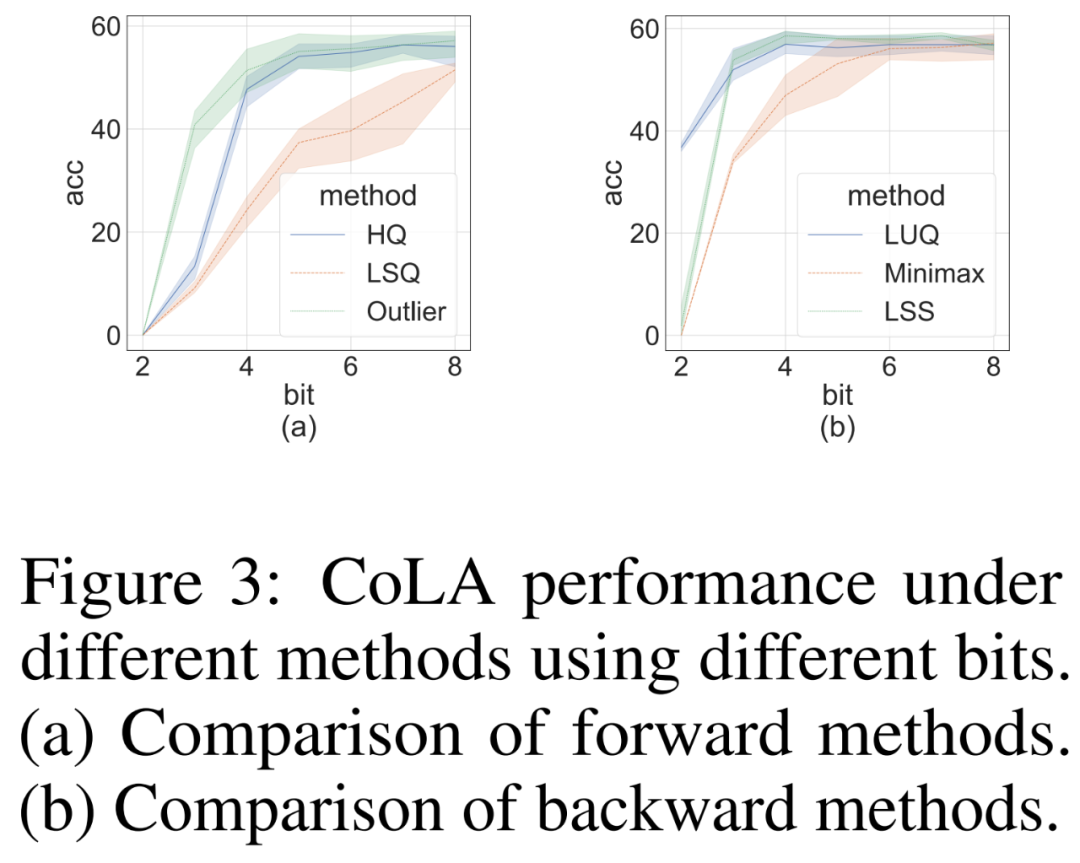
Wir haben Ablationsstudien durchgeführt, um unabhängig die Wirksamkeit von Vorwärts- und Rückwärtsmethoden bei anspruchsvollen CoLA-Datensätzen zu demonstrieren. Um die Wirksamkeit verschiedener Quantisierer bei der Vorwärtsausbreitung zu untersuchen, setzten sie die Rückausbreitung auf FP16. Die Ergebnisse sind in Abbildung 3(a) unten dargestellt.
Für die Backpropagation verglichen die Forscher einen einfachen Minimax-Quantisierer, LUQ, und ihr eigenes LSS und stellten die Forward-Propagation auf FP16 ein. Die Ergebnisse sind in Abbildung 3 (b) unten dargestellt. Obwohl die Bitbreite höher als 2 ist, erzielt LSS Ergebnisse, die mit LUQ vergleichbar oder sogar etwas besser sind.
Bilder
Rechen- und Speichereffizienz
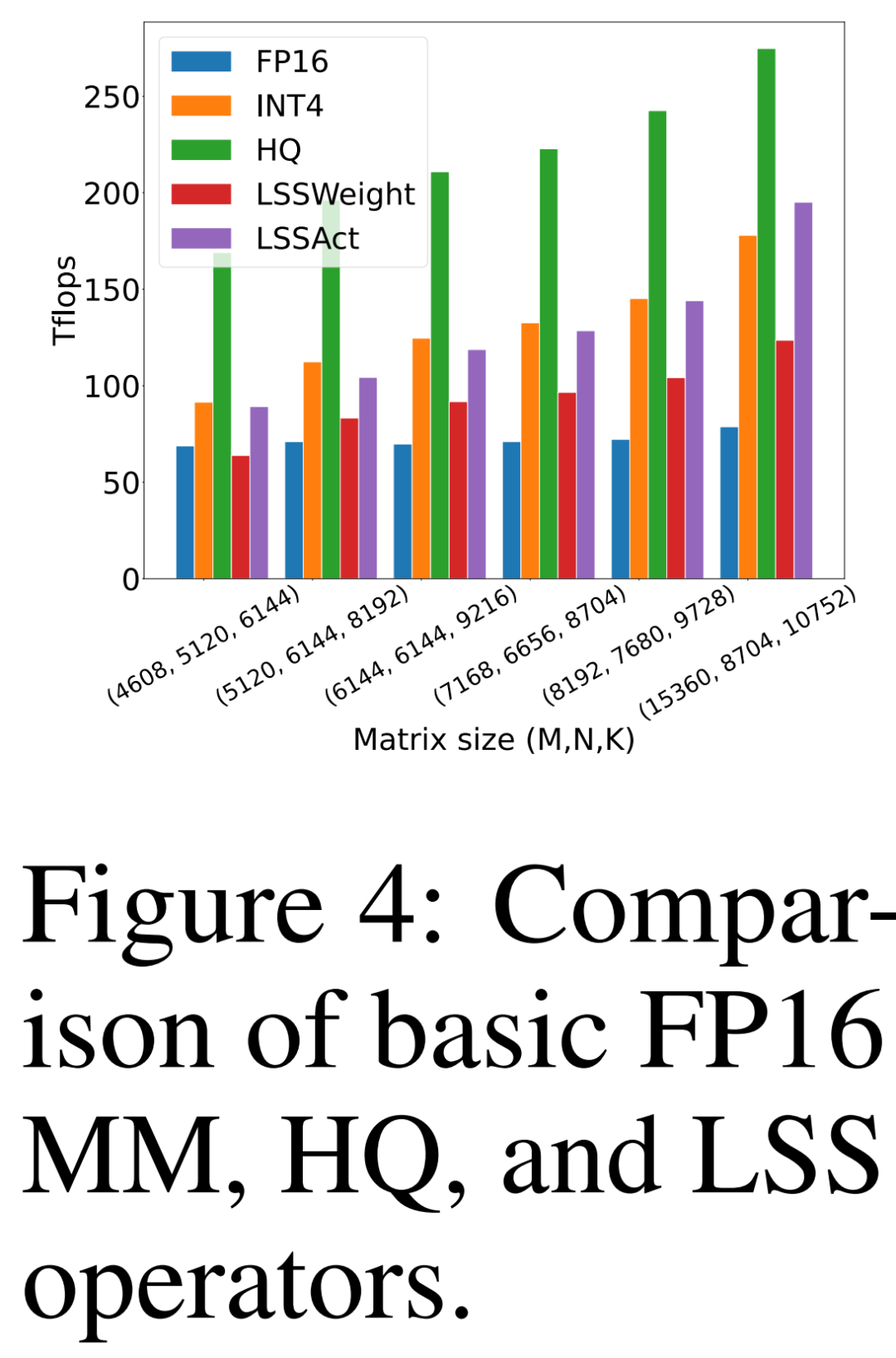
Die Forscher verglichen ihr eigenes vorgeschlagenes HQ-MM (HQ), LSS zur Berechnung von Gewichtsgradienten (LSSWeight) und LSS zur Berechnung von Aktivierungsgradienten (LSSAct). ) Durchsatz, ihr durchschnittlicher Durchsatz (INT4) und die grundlegende Tensor Core FP16 GEMM-Implementierung (FP16), die von Cutlass auf der NVIDIA RTX 3090 GPU in Abbildung 4 unten bereitgestellt wird und einen Spitzendurchsatz von 142 FP16 TFLOPs und 568 INT4 TFLOPs aufweist.
Bilder
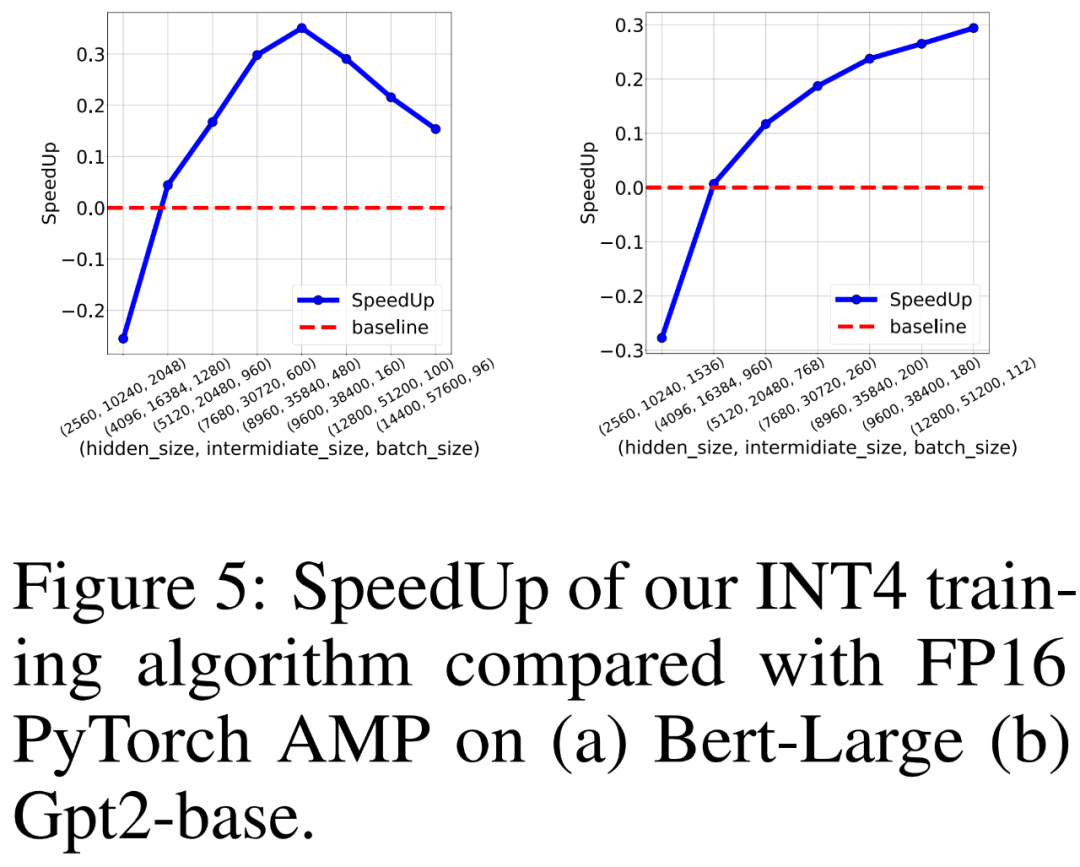
Die Forscher verglichen auch den Trainingsdurchsatz von FP16 PyTorch AMP und ihrem eigenen INT4-Trainingsalgorithmus zum Training von BERT-ähnlichen und GPT-ähnlichen Sprachmodellen auf 8 NVIDIA A100-GPUs. Sie variierten die Größe der verborgenen Schicht, die Größe der vollständig verbundenen Zwischenschicht und die Stapelgröße und zeichneten die Beschleunigung für das INT4-Training in Abbildung 5 unten auf.
Die Ergebnisse zeigen, dass der INT4-Trainingsalgorithmus eine Beschleunigung von bis zu 35,1 % für BERT-ähnliche Modelle und eine Beschleunigung von bis zu 26,5 % für GPT-ähnliche Modelle erreicht.
Bilder
Das obige ist der detaillierte Inhalt vonDas GPT-ähnliche Modelltraining wird um 26,5 % beschleunigt. Tsinghua Zhu Jun und andere verwenden den INT4-Algorithmus, um das Training neuronaler Netzwerke zu beschleunigen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
Algorithmus zum Ersetzen von Seiten
Die Rolle des Füllattributs in CSS
Welche Datentypen gibt es?
Was sind die grundlegenden Datentypen in PHP?
Alle Verwendungen von Cloud-Servern
Was soll ich tun, wenn sich die Maus nicht mehr bewegt?
Detaillierte Erklärung des Befehls imp in Oracle
So überprüfen Sie tote Links auf Ihrer Website
