Häufig verwendete Verlustfunktionen und Python-Implementierungsbeispiele

Was ist die Verlustfunktion?

Die Verlustfunktion ist ein Algorithmus, der den Grad der Übereinstimmung zwischen dem Modell und den Daten misst. Eine Verlustfunktion ist eine Möglichkeit, die Differenz zwischen tatsächlichen Messungen und vorhergesagten Werten zu messen. Je höher der Wert der Verlustfunktion, desto fehlerhafter ist die Vorhersage, und je niedriger der Wert der Verlustfunktion, desto näher liegt die Vorhersage am wahren Wert. Die Verlustfunktion wird für jede einzelne Beobachtung (Datenpunkt) berechnet. Die Funktion, die die Werte aller Verlustfunktionen mittelt, wird als Kostenfunktion bezeichnet. Ein einfacheres Verständnis besteht darin, dass die Verlustfunktion für eine einzelne Stichprobe gilt, während die Kostenfunktion für alle Stichproben gilt.

Verlustfunktionen und Metriken

Einige Verlustfunktionen können auch als Bewertungsmetriken verwendet werden. Aber Verlustfunktionen und Metriken haben unterschiedliche Zwecke. Während Metriken verwendet werden, um das endgültige Modell zu bewerten und die Leistung verschiedener Modelle zu vergleichen, wird die Verlustfunktion während der Modellerstellungsphase als Optimierer für das zu erstellende Modell verwendet. Die Verlustfunktion leitet das Modell an, wie der Fehler minimiert werden kann.

Das heißt, die Verlustfunktion weiß, wie das Modell trainiert wird, und der Messindex erklärt die Leistung des Modells

Warum die Verlustfunktion verwenden?#🎜🎜 ##🎜🎜 #Da die Verlustfunktion die Differenz zwischen dem vorhergesagten Wert und dem tatsächlichen Wert misst, können sie beim Training des Modells als Leitfaden für die Modellverbesserung (die übliche Gradientenabstiegsmethode) verwendet werden. Wenn sich beim Erstellen des Modells das Gewicht des Merkmals ändert und bessere oder schlechtere Vorhersagen getroffen werden, müssen Sie die Verlustfunktion verwenden, um zu beurteilen, ob das Gewicht des Merkmals im Modell geändert werden muss und in welche Richtung die Änderung geht .

Wir können beim maschinellen Lernen verschiedene Verlustfunktionen verwenden, abhängig von der Art des Problems, das wir lösen möchten, der Datenqualität und -verteilung sowie dem von uns verwendeten Algorithmus habe 10 gängige Verlustfunktionen zusammengestellt:

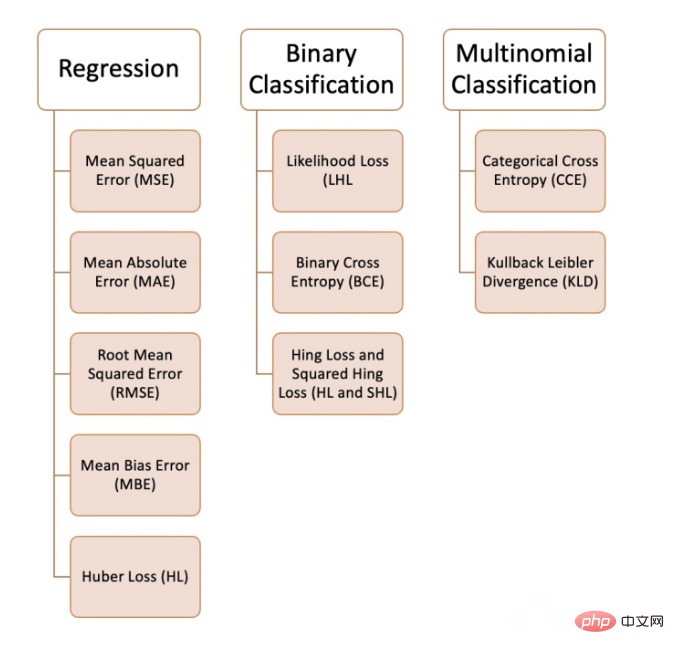Regressionsproblem

1 Mittlerer quadratischer Fehler (MSE)

def MSE (y, y_predicted):
 sq_error = (y_predicted - y) ** 2
 sum_sq_error = np.sum(sq_error)
 mse = sum_sq_error/y.size
 return mse

Nach dem Login kopieren

def MAE (y, y_predicted):
 error = y_predicted - y
 absolute_error = np.absolute(error)
 total_absolute_error = np.sum(absolute_error)
 mae = total_absolute_error/y.size
 return mae

Nach dem Login kopieren

def RMSE (y, y_predicted):
 sq_error = (y_predicted - y) ** 2
 total_sq_error = np.sum(sq_error)
 mse = total_sq_error/y.size
 rmse = math.sqrt(mse)
 return rmse

Nach dem Login kopieren

def MBE (y, y_predicted):
 error = y_predicted -y
 total_error = np.sum(error)
 mbe = total_error/y.size
 return mbe

Nach dem Login kopieren

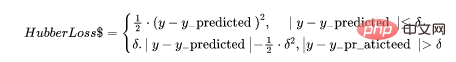
def hubber_loss (y, y_predicted, delta)
 delta = 1.35 * MAE
 y_size = y.size
 total_error = 0
 for i in range (y_size):
erro = np.absolute(y_predicted[i] - y[i])
if error < delta:
 hubber_error = (error * error) / 2
else:
 hubber_error = (delta * error) / (0.5 * (delta * delta))
total_error += hubber_error
 total_hubber_error = total_error/y.size
 return total_hubber_error

6. Maximum-Likelihood-Verlust (Likelihood Loss/LHL)

Diese Verlustfunktion wird hauptsächlich für binäre Klassifizierungsprobleme verwendet. Die Wahrscheinlichkeit jedes vorhergesagten Werts wird multipliziert, um einen Verlustwert zu erhalten, und die zugehörige Kostenfunktion ist der Durchschnitt aller beobachteten Werte. Nehmen wir das folgende Beispiel einer binären Klassifizierung, bei der die Klasse [0] oder [1] ist. Wenn die Ausgabewahrscheinlichkeit gleich oder größer als 0,5 ist, ist die vorhergesagte Klasse [1], andernfalls ist sie [0]. Ein Beispiel für die Ausgabewahrscheinlichkeit lautet wie folgt:

[0.3 , 0.7 , 0.8 , 0.5 , 0.6 , 0.4]

Die entsprechende vorhergesagte Klasse ist:

[0 , 1 , 1 , 1 , 1 , 0]

Und die tatsächliche Klasse ist:

[0 , 1 , 1 , 0 , 1 , 0]

Jetzt Zur Berechnung des Verlusts werden die realen Klassen- und Ausgabewahrscheinlichkeiten verwendet. Wenn die wahre Klasse [1] ist, verwenden wir die Ausgabewahrscheinlichkeit, wenn die wahre Klasse [0] ist, verwenden wir die 1-Wahrscheinlichkeit:

((1–0.3)+0.7+0.8+(1–0.5)+0.6+(1–0.4)) / 6 = 0.65

Der Python-Code lautet wie folgt: #🎜🎜 #

def LHL (y, y_predicted):
 likelihood_loss = (y * y_predicted) + ((1-y) * (y_predicted))
 total_likelihood_loss = np.sum(likelihood_loss)
 lhl = - total_likelihood_loss / y.size
 return lhl

Lassen Sie uns weiterhin die Werte aus verwenden obiges Beispiel: #🎜 🎜#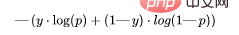

1. (0 . log (0,3) + (1–0) . log (1–0,3)) = 0,155
#🎜 🎜#(1 . log(0,7) + (1–1) . log (0,3)) = 0,155
(1 . log(0,8) + (1–1) . log (0,2)) = 0,097#🎜 🎜#

• (1 . log(0,6) + ( 1–1). ##🎜🎜 #Dann ist das Ergebnis der Kostenfunktion:

(0.155 + 0.155 + 0.097 + 0.301 + 0.222 + 0.222) / 6 = 0.192

Nach dem Login kopieren
• Der Python-Code lautet wie folgt:

def BCE (y, y_predicted):
 ce_loss = y*(np.log(y_predicted))+(1-y)*(np.log(1-y_predicted))
 total_ce = np.sum(ce_loss)
 bce = - total_ce/y.size
 return bce

Nach dem Login kopieren
• 8, Hinge Loss und Squared Hinge Loss (HL und SHL)
#🎜 🎜#Hinge Loss wird als Scharnierverlust oder Scharnierverlust übersetzt. Hier ist die englische Version maßgebend.

• Hinge Loss主要用于支持向量机模型的评估。错误的预测和不太自信的正确预测都会受到惩罚。所以一般损失函数是：

  

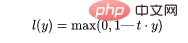
  这里的t是真实结果用[1]或[-1]表示。

  使用Hinge Loss的类应该是[1]或-1。为了在Hinge loss函数中不被惩罚，一个观测不仅需要正确分类而且到超平面的距离应该大于margin(一个自信的正确预测)。如果我们想进一步惩罚更高的误差，我们可以用与MSE类似的方法平方Hinge损失,也就是Squared Hinge Loss。

  如果你对SVM比较熟悉，应该还记得在SVM中，超平面的边缘（margin）越高，则某一预测就越有信心。如果这块不熟悉，则看看这个可视化的例子:

  

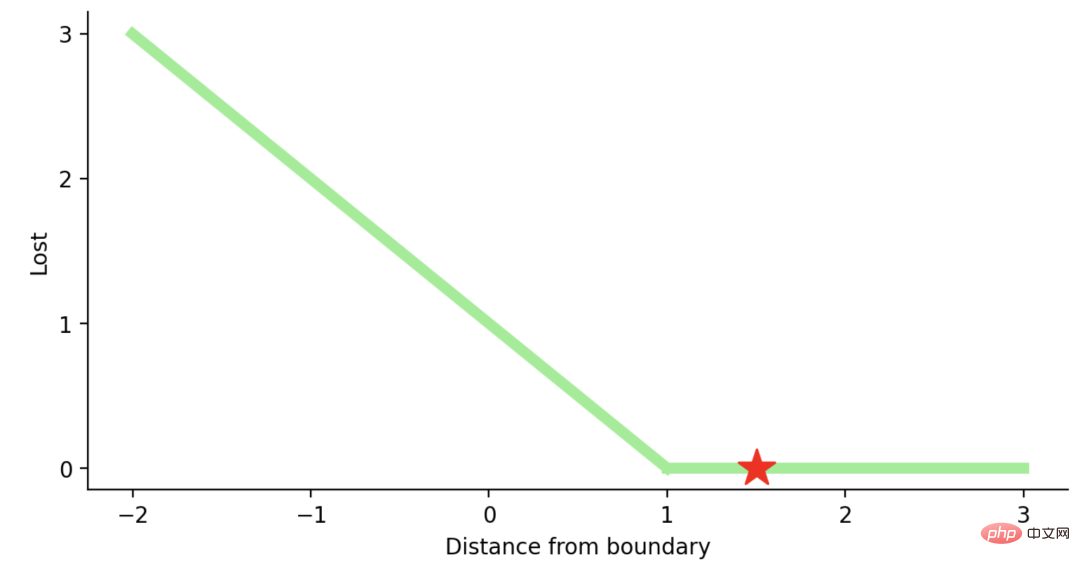
  如果一个预测的结果是1.5，并且真正的类是[1]，损失将是0(零)，因为模型是高度自信的。

  loss= Max (0,1 - 1* 1.5) = Max (0， -0.5) = 0

  

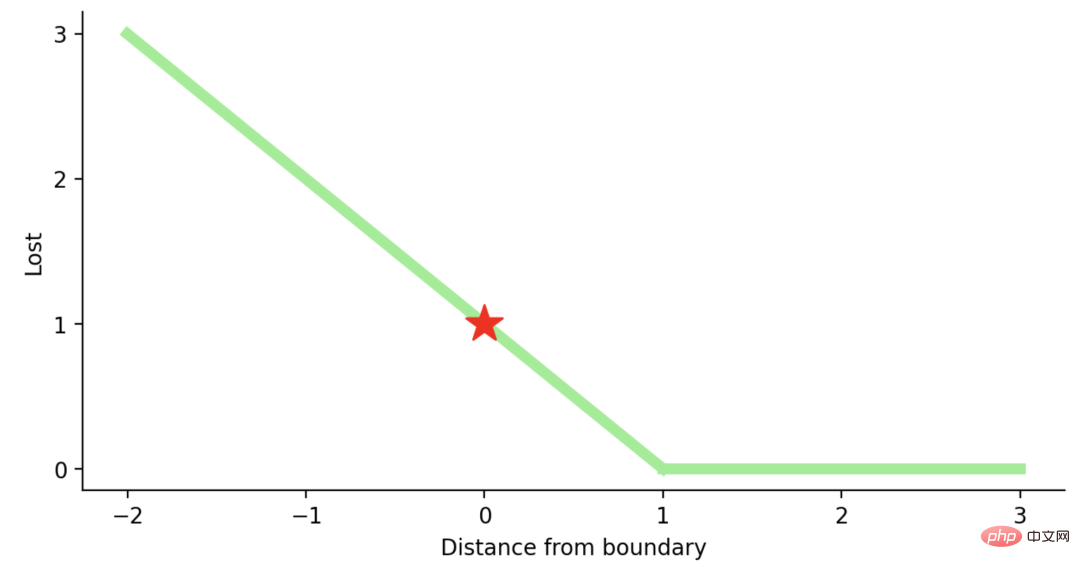
  如果一个观测结果为0(0)，则表示该观测处于边界(超平面)，真实的类为[-1]。损失为1，模型既不正确也不错误，可信度很低。

  

  

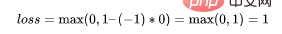
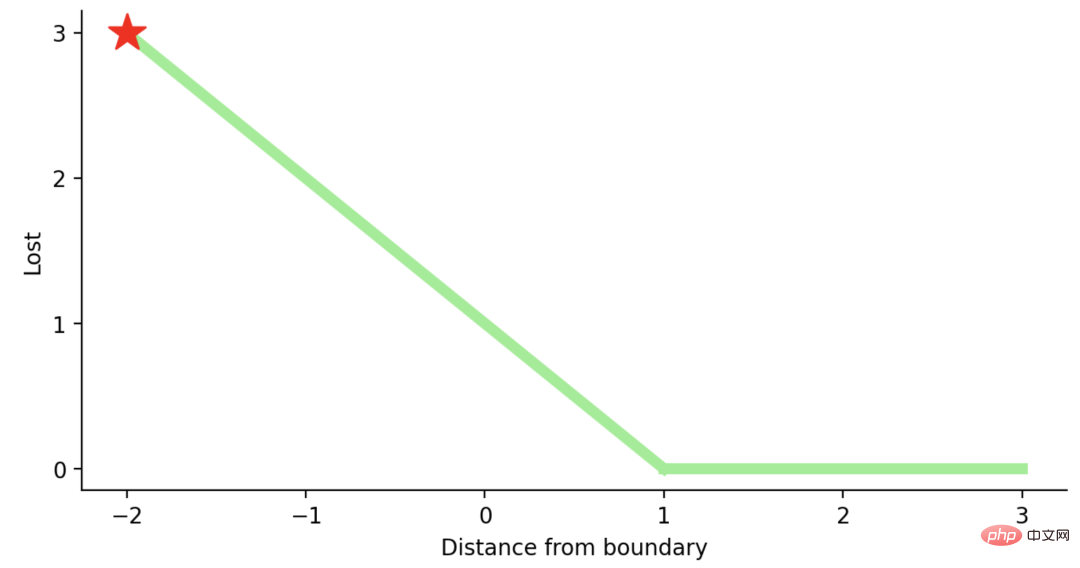
  如果一次观测结果为2，但分类错误(乘以[-1])，则距离为-2。损失是3(非常高)，因为我们的模型对错误的决策非常有信心（这个是绝不能容忍的）。

  

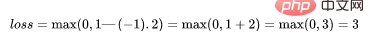
  python代码如下：

  #Hinge Loss 
  def Hinge (y, y_predicted): 
   hinge_loss = np.sum(max(0 , 1 - (y_predicted * y))) 
   return hinge_loss 
  
  #Squared Hinge Loss 
  def SqHinge (y, y_predicted): 
   sq_hinge_loss = max (0 , 1 - (y_predicted * y)) ** 2 
   total_sq_hinge_loss = np.sum(sq_hinge_loss) 
   return total_sq_hinge_loss

  Nach dem Login kopieren

  多分类

  9、交叉熵（CE）

  在多分类中，我们使用与二元交叉熵类似的公式，但有一个额外的步骤。首先需要计算每一对[y, y_predicted]的损失，一般公式为：

  

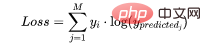
  如果我们有三个类，其中单个[y, y_predicted]对的输出是：

  

  这里实际的类3（也就是值=1的部分），我们的模型对真正的类是3的信任度是0.7。计算这损失如下：

  

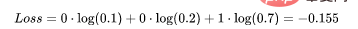
  为了得到代价函数的值，我们需要计算所有单个配对的损失，然后将它们相加最后乘以[-1/样本数量]。代价函数由下式给出：

  

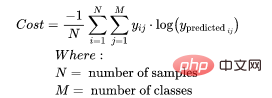
  使用上面的例子，如果我们的第二对：

  

  那么成本函数计算如下：

  

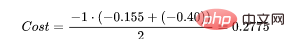
  使用Python的代码示例可以更容易理解；

  def CCE (y, y_predicted): 
   cce_class = y * (np.log(y_predicted)) 
   sum_totalpair_cce = np.sum(cce_class) 
   cce = - sum_totalpair_cce / y.size 
   return cce

  Nach dem Login kopieren

  10、Kullback-Leibler 散度 (KLD)

  又被简化称为KL散度，它类似于分类交叉熵，但考虑了观测值发生的概率。如果我们的类不平衡，它特别有用。

  

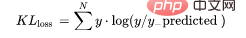
  def KL (y, y_predicted): 
   kl = y * (np.log(y / y_predicted)) 
   total_kl = np.sum(kl) 
   return total_kl

  Nach dem Login kopieren

  以上就是常见的10个损失函数，希望对你有所帮助。

  Das obige ist der detaillierte Inhalt vonHäufig verwendete Verlustfunktionen und Python-Implementierungsbeispiele. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!