常见降维技术对比：保持信息完整性下降低数据维度的可行性分析-KI-php.cn

本文将比较各种降维技术在机器学习任务中对表格数据的有效性。我们将降维方法应用于数据集，并通过回归和分类分析评估其有效性。我们将降维方法应用于从与不同领域相关的 UCI 中获取的各种数据集。总共选择了 15 个数据集，其中 7 个将用于回归，8 个用于分类。

常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

为了使本文易于阅读和理解，仅显示了一个数据集的预处理和分析。实验从加载数据集开始。数据集被分成训练集和测试集，然后在均值为 0 且标准差为 1 的情况下进行标准化。

然后会将降维技术应用于训练数据，并使用相同的参数对测试集进行变换以进行降维。对于回归，使用主成分分析（PCA）和奇异值分解（SVD）进行降维，另一方面对于分类，使用线性判别分析（LDA）

降维后就训练多个机器学习模型进行测试，并比较了不同模型在通过不同降维方法获得的不同数据集上的性能。

数据处理

让我们通过加载第一个数据集开始这个过程，

import pandas as pd ## for data manipulation df = pd.read_excel(r'RegressionAirQualityUCI.xlsx') print(df.shape) df.head()

Nach dem Login kopieren

常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

数据集包含15个列，其中一个是需要预测标签。在继续降维之前，日期和时间列也会被删除。

X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1) y = df['CO(GT)'] X.shape, y.shape #Output: ((9357, 12), (9357,))

Nach dem Login kopieren

为了训练，我们需要将数据集划分为训练集和测试集，这样可以评估降维方法和在降维特征空间上训练的机器学习模型的有效性。模型将使用训练集进行训练，性能将使用测试集进行评估。

from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) X_train.shape, X_test.shape, y_train.shape, y_test.shape #Output: ((7485, 12), (1872, 12), (7485,), (1872,))

Nach dem Login kopieren

在对数据集使用降维技术之前，可以对输入数据进行缩放，这样可以保证所有特征处于相同的比例上。这对于线性模型来说是是至关重要的，因为某些降维方法可以根据数据是否标准化以及对特征的大小敏感而改变其输出。

from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) X_train.shape, X_test.shape

Nach dem Login kopieren

主成分分析(PCA)

线性降维的PCA方法降低了数据的维数，同时保留了尽可能多的数据方差。

这里将使用Python sklearn.decomposition模块的PCA方法。要保留的组件数量是通过这个参数指定的，这个数字会影响在较小的特征空间中包含多少维度。作为一种替代方法，我们可以设定要保留的目标方差，它根据捕获的数据中的方差量建立组件的数量，我们这里设置为0.95

from sklearn.decomposition import PCA pca = PCA(n_compnotallow=0.95) X_train_pca = pca.fit_transform(X_train) X_test_pca = pca.transform(X_test) X_train_pca

Nach dem Login kopieren

常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

上述特征代表什么?主成分分析(PCA)将数据投射到低维空间，试图尽可能多地保留数据中的不同之处。虽然这可能有助于特定的操作，但也可能使数据更难以理解。，PCA可以识别数据中的新轴，这些轴是初始特征的线性融合。

奇异值分解(SVD)

SVD是一种线性降维技术，它将数据方差较小的特征投影到低维空间。我们需要设置降维后要保留的组件数量。这里我们将把维度降低 2/3。

from sklearn.decomposition import TruncatedSVD svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33)) X_train_svd = svd.fit_transform(X_train) X_test_svd = svd.transform(X_test) X_train_svd

Nach dem Login kopieren

常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

训练回归模型

现在，我们将开始使用上述三种数据(原始数据集、PCA和SVD)对模型进行训练和测试，并且我们使用多个模型进行对比。

import numpy as np from sklearn.linear_model import LinearRegression from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import SVR from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor from sklearn.metrics import r2_score, mean_squared_error import time

Nach dem Login kopieren

train_test_ML:这个函数将完成与模型的训练和测试相关的重复任务。通过计算rmse和r2_score来评估所有模型的性能。并返回包含所有详细信息和计算值的数据集，还将记录每个模型在各自的数据集上训练和测试所花费的时间。

def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test): temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken']) for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]: start_time = time.time() reg = i().fit(X_train, y_train) y_pred = reg.predict(X_test) r2 = np.round(r2_score(y_test, y_pred), 2) rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2) end_time = time.time() time_taken = np.round((end_time - start_time), 2) temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken] return temp_df

Nach dem Login kopieren

原始数据:

original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test) original_df

Nach dem Login kopieren

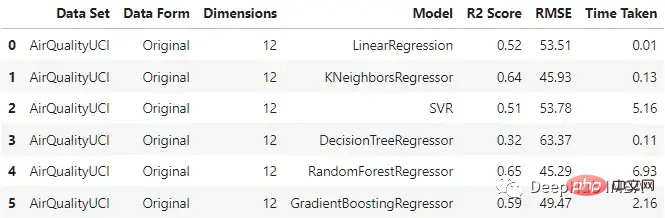
常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

可以看到KNN回归器和随机森林在输入原始数据时表现相对较好，随机森林的训练时间是最长的。

PCA

pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test) pca_df

Nach dem Login kopieren

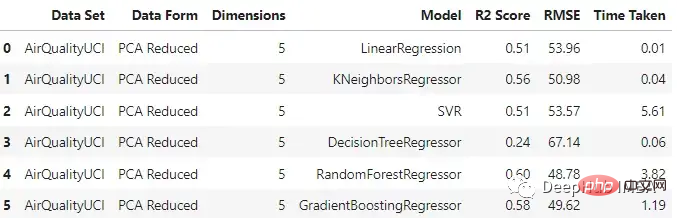
常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

与原始数据集相比，不同模型的性能有不同程度的下降。梯度增强回归和支持向量回归在两种情况下保持了一致性。这里一个主要的差异也是预期的是模型训练所花费的时间。与其他模型不同的是，SVR在这两种情况下花费的时间差不多。

SVD

svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test) svd_df

Nach dem Login kopieren

常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

与PCA相比，SVD以更大的比例降低了维度，随机森林和梯度增强回归器的表现相对优于其他模型。

回归模型分析

对于这个数据集，使用主成分分析时，数据维数从12维降至5维，使用奇异值分析时，数据降至3维。

就机器学习性能而言，数据集的原始形式相对更好。造成这种情况的一个潜在原因可能是，当我们使用这种技术降低维数时，在这个过程中会发生信息损失。
但是线性回归、支持向量回归和梯度增强回归在原始和PCA案例中的表现是一致的。
在我们通过SVD得到的数据上，所有模型的性能都下降了。
在降维情况下，由于特征变量的维数较低，模型所花费的时间减少了。

将类似的过程应用于其他六个数据集进行测试，得到以下结果:

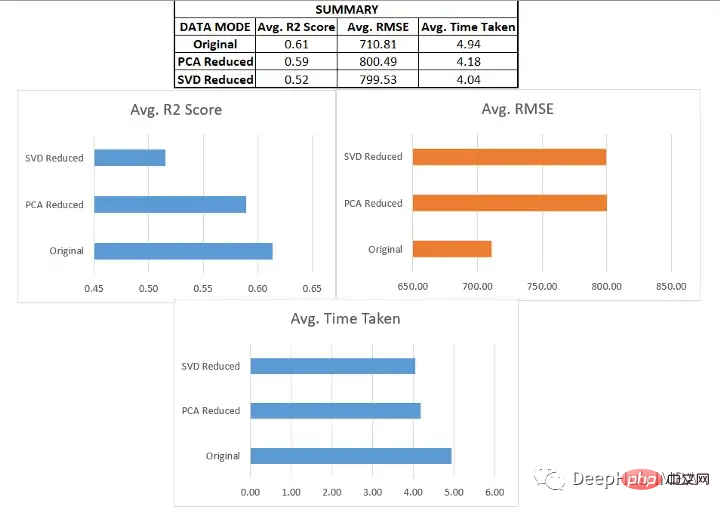
常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

我们在各种数据集上使用了SVD和PCA，并对比了在原始高维特征空间上训练的回归模型与在约简特征空间上训练的模型的有效性

原始数据集始终优于由降维方法创建的低维数据。这说明在降维过程中可能丢失了一些信息。
当用于更大的数据集时，降维方法有助于显著减少数据集中的特征数量，从而提高机器学习模型的有效性。对于较小的数据集，改影响并不显著。
模型的性能在original和pca_reduced两种模式下保持一致。如果一个模型在原始数据集上表现得更好，那么它在PCA模式下也会表现得更好。同样，较差的模型也没有得到改进。
在SVD的情况下，模型的性能下降比较明显。这可能是n_components数量选择的问题，因为太小数量肯定会丢失数据。
决策树在SVD数据集时一直是非常差的，因为它本来就是一个弱学习器

训练分类模型

对于分类我们将使用另一种降维方法：LDA。机器学习和模式识别任务经常使用被称为线性判别分析(LDA)的降维方法。这种监督学习技术旨在最大化几个类或类别之间的距离，同时将数据投影到低维空间。由于它的作用是最大化类之间的差异，因此只能用于分类任务。

from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.svm import SVC from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score

Nach dem Login kopieren

继续我们的训练方法

def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test): temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken']) for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]: start_time = time.time() reg = i().fit(X_train, y_train) y_pred = reg.predict(X_test) accuracy = np.round(accuracy_score(y_test, y_pred), 2) f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2) recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2) precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2) end_time = time.time() time_taken = np.round((end_time - start_time), 2) temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken] return temp_df

Nach dem Login kopieren

开始训练

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis lda = LinearDiscriminantAnalysis() X_train_lda = lda.fit_transform(X_train, y_train) X_test_lda = lda.transform(X_test)

Nach dem Login kopieren

预处理、分割和数据集的缩放，都与回归部分相同。在对8个不同的数据集进行新联后我们得到了下面结果:

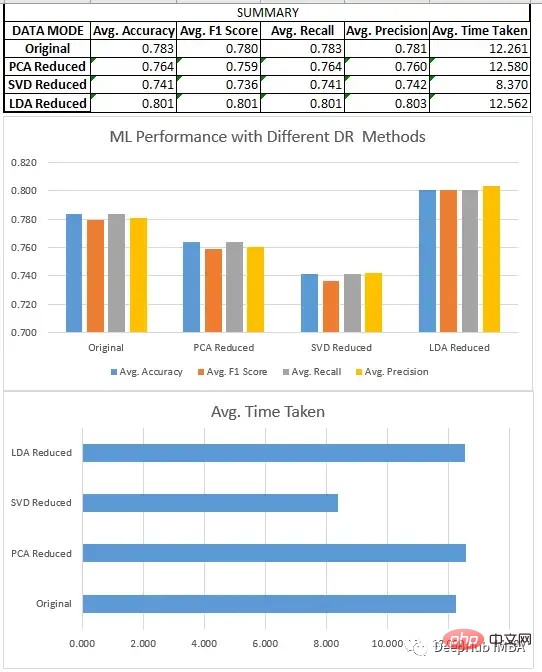
常见的降维技术比较：能否在不丢失信息的情况下降低数据维度

分类模型分析

我们比较了上面所有的三种方法SVD、LDA和PCA。

LDA数据集通常优于原始形式的数据和由其他降维方法创建的低维数据，因为它旨在识别最有效区分类的特征的线性组合，而原始数据和其他无监督降维技术不关心数据集的标签。
降维技术在应用于更大的数据集时，可以极大地减少了数据集中的特征数量，这提高了机器学习模型的效率。在较小的数据集上，影响不是特别明显。除了LDA（它在这些情况下也很有效），因为它们在一些情况下，如二元分类，可以将数据集的维度减少到只有一个。
当我们在寻找一定的性能时，LDA可以是分类问题的一个非常好的起点。
SVD与回归一样，模型的性能下降很明显。需要调整n_components的选择。

总结

我们比较了一些降维技术的性能，如奇异值分解(SVD)、主成分分析(PCA)和线性判别分析(LDA)。我们的研究结果表明，方法的选择取决于特定的数据集和手头的任务。

对于回归任务，我们发现PCA通常比SVD表现得更好。在分类的情况下，LDA优于SVD和PCA，以及原始数据集。线性判别分析(LDA)在分类任务中始终击败主成分分析(PCA)的这个是很重要的，但这并不意味着LDA在一般情况下是一种更好的技术。这是因为LDA是一种监督学习算法，它依赖于有标签的数据来定位数据中最具鉴别性的特征，而PCA是一种无监督技术，它不需要有标签的数据，并寻求在数据中保持尽可能多的方差。因此，PCA可能更适合于无监督的任务或可解释性至关重要的情况，而LDA可能更适合涉及标记数据的任务。

虽然降维技术可以帮助减少数据集中的特征数量，并提高机器学习模型的效率，但重要的是要考虑对模型性能和结果可解释性的潜在影响。

本文完整代码：

https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb

Das obige ist der detaillierte Inhalt von常见降维技术对比：保持信息完整性下降低数据维度的可行性分析. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!