
Stack (Stack) ist eine Last-In-First-Off-Datenstruktur (LIFO). Stapel (Stack)
Es können nur Elemente an einem Ende hinzugefügt und Elemente an einem Ende entfernt werden (dieses Ende wird als oberstes Ende des Stapels bezeichnet).
| void push(E e) | Elemente zum Stapel hinzufügen | |
|---|---|---|
| E pop() | Das oberste Element des Stapels platzen lassenO(1) | Gleichmäßig verteilen|
| E peek() | Das oberste Element des Stapels anzeigenO(1) | |
| int getSize() | Erhalten Sie die Anzahl der Elemente im Stapel | O(1) |
| boolean isEmpty() | Beurteilen Sie, ob der Stapel leer ist | O(1) |
| Erläuterung: drücken und Pop-Operationen werden am Ende ausgeführt, es ist möglich, die Größe zu ändern, aber die gleichmäßige Verteilung ist O(1). | Wenn Sie mehr über die Zeitkomplexitätsanalyse erfahren möchten, beachten Sie bitte den Artikel, den der Autor später aktualisieren wird: | Welches Problem erklärt O(n)?
Stack
dies verwenden Datenstruktur zur Lösung von Problem Nr. 20 auf LeetCode: Für gültige Klammern siehe auch Tägliche Zählung: Gültige Klammern. Queue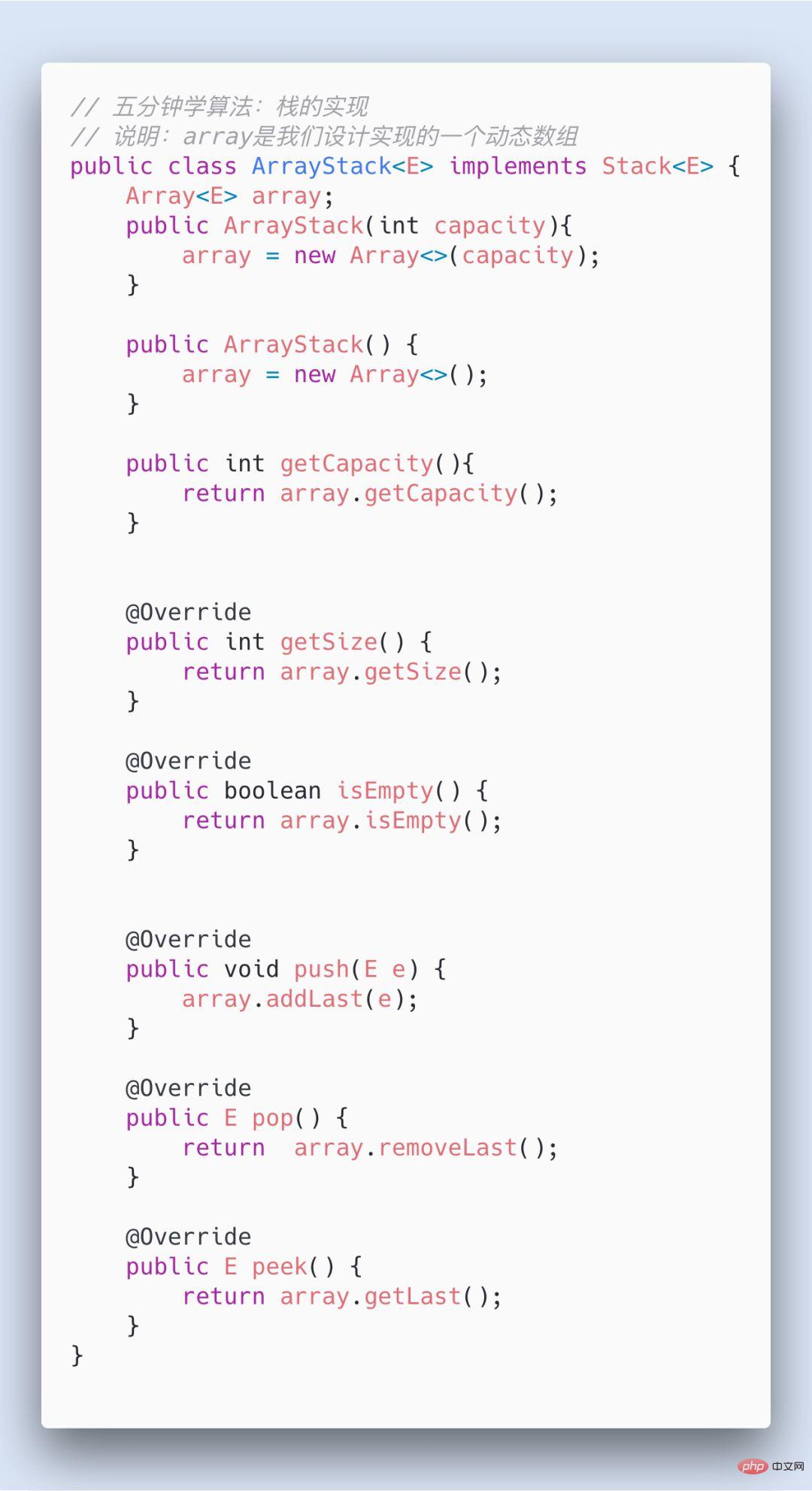 Queue ist auch eine lineare Datenstruktur. Im Vergleich zu Arrays sind die Operationen, die Warteschlangen entsprechen, eine Teilmenge von Arrays.
Queue ist auch eine lineare Datenstruktur. Im Vergleich zu Arrays sind die Operationen, die Warteschlangen entsprechen, eine Teilmenge von Arrays.
Elemente können nur von einem Ende (dem Ende der Warteschlange) hinzugefügt werden und Elemente können nur vom anderen Ende (dem Kopf der Warteschlange) herausgenommen werden. Die Anwendung der Warteschlange kann sich in der Wiedergabeliste des Players, im Datenstromobjekt und in der asynchronen Datenübertragungsstruktur (Datei-E/A, Pipe-Kommunikation, Socket usw.) widerspiegeln. Die intuitivste Methode ist natürlich die Warteschlange.
| void enqueue(E e) | enqueue | |
|---|---|---|
| E dequeue( ) | Aus der Warteschlange entfernenO(n) | |
| E getFront() | Das erste Element der Warteschlange abrufen | O(1) |
| int getSize() | Die Anzahl der Warteschlangenelemente abrufen | O( 1) |
| boolean isEmpty() | Bestimmen Sie, ob die Warteschlange leer ist | O(1) |
| Der Eintritt in die Warteschlange beginnt am Ende der Warteschlange, und eine Größenänderung kann daher ausgelöst werden ist im Durchschnitt O(1). Das Entfernen aus der Warteschlange erfolgt an der Spitze der Warteschlange, und die Array-Implementierung erfordert jedes Mal das Verschieben aller Elemente, O(n). |
Das obige ist der detaillierte Inhalt vonSo implementieren Sie Java-Stack und -Warteschlange. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




