
Bildverarbeitung ist zu einem integralen Bestandteil unseres täglichen Lebens geworden und umfasst verschiedene Bereiche wie soziale Medien und medizinische Bildgebung. Bilder, die von Digitalkameras oder anderen Quellen wie Satellitenfotos und medizinischen Scans stammen, müssen möglicherweise vorverarbeitet werden, um Rauschen zu entfernen oder zu verstärken. Frequenzbereichsfilterung ist eine mögliche Lösung, die Rauschen entfernen und gleichzeitig die Bildschärfe verbessern kann.
Die schnelle Fourier-Transformation (FFT) ist eine mathematische Technik, die Bilder vom räumlichen Bereich in den Frequenzbereich transformiert. Sie ist ein Schlüsselwerkzeug für die Frequenztransformation in der Bildverarbeitung. Durch die Verwendung einer Frequenzbereichsdarstellung eines Bildes können wir das Bild effektiv anhand seines Frequenzinhalts analysieren und so die Anwendung von Filterverfahren zur Rauschentfernung vereinfachen. In diesem Artikel werden die verschiedenen Phasen der Frequenztransformation eines Bildes von FFT zu inverser FFT in Kombination mit der Verwendung von FFT-Verschiebung und inverser FFT-Verschiebung erläutert.
Dieser Artikel verwendet drei Python-Bibliotheken, nämlich openCV, Numpy und Matplotlib.
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('sample.png',0) # Using 0 to read image in grayscale mode
plt.imshow(img, cmap='gray')#cmap is used to specify imshow that the image is in greyscale
plt.xticks([]), plt.yticks([])# remove tick marks
plt.show()
f = np.fft.fft2(img)#the image 'img' is passed to np.fft.fft2() to compute its 2D Discrete Fourier transform f
mag = 20*np.log(np.abs(f))
plt.imshow(mag, cmap = 'gray') #cmap='gray' parameter to indicate that the image should be displayed in grayscale.
plt.title('Magnitude Spectrum')
plt.xticks([]), plt.yticks([])
plt.show()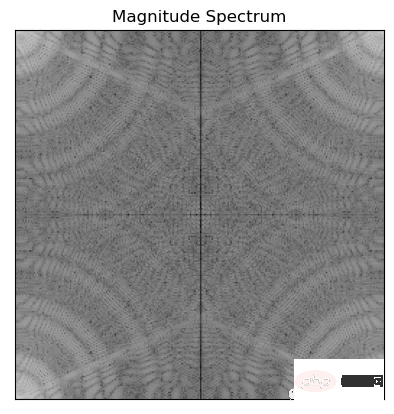
2. FFT-Verschiebung
3. Filterung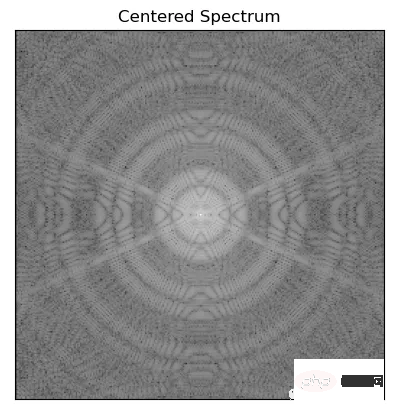
Im Frequenzbereich beträgt der Amplituden-Frequenzgang eines idealen Filters:
Im Durchlassbereich beträgt der Amplituden-Frequenzgang 1Im Sperrbereich beträgt der Amplituden-Frequenzgang 0Der Frequenzgang des Gaußschen Hochpassfilters kann ausgedrückt werden als:
H(u,v) = 1 - L(u,v)
wobei L(u,v) ein Tiefpassfilter ist , die als Gaußsche Funktionsdarstellung verwendet werden kann. Die Reaktion eines Hochpassfilters wird durch Subtrahieren der Reaktion des Tiefpassfilters von 1 ermittelt. In der Praxis werden normalerweise unterschiedliche Parametereinstellungen verwendet, um die Gaußsche Funktion anzupassen und unterschiedliche Filtereffekte zu erzielen.
Scheibenförmige Bilder werden verwendet, um die Frequenzkomponenten zu definieren, die beibehalten oder unterdrückt werden sollen, wenn im Bild eine Fourier-Transformation durchgeführt wird. In diesem Zusammenhang bezieht sich ein idealer Filter normalerweise auf einen idealen Tiefpass- oder Hochpassfilter, der im Frequenzbereich ausgewählt werden kann, um Signale innerhalb eines bestimmten Frequenzbereichs zurückzuhalten oder zu unterdrücken. Nach Anwendung dieses idealen Filters auf die Fourier-Transformation des Bildes und anschließender Durchführung der Rücktransformation kann das vom Filter verarbeitete Bild erhalten werden.
Wir werden die spezifischen Details nicht vorstellen, schauen wir uns den Code direkt an:
Die folgende Funktion generiert eine kreisförmige Maske für ideale Hochpass- und Tiefpassfilter
fshift = np.fft.fftshift(f)
mag = 20*np.log(np.abs(fshift))
plt.imshow(mag, cmap = 'gray')
plt.title('Centered Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()Die folgende Funktion generiert einen Gaußschen Hoch- Pass- und Tiefpassfilter Filterbeispiel
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def idealFilterLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 1 return base def idealFilterHP(D0,imgShape): base = np.ones(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): if distance((y,x),center) < D0: base[y,x] = 0 return base
import math def distance(point1,point2): return math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2) def gaussianLP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base def gaussianHP(D0,imgShape): base = np.zeros(imgShape[:2]) rows, cols = imgShape[:2] center = (rows/2,cols/2) for x in range(cols): for y in range(rows): base[y,x] = 1 - math.exp(((-distance((y,x),center)**2)/(2*(D0**2)))) return base

相乘过滤器和移位的图像得到过滤图像
为了获得具有所需频率响应的最终滤波图像,关键是在频域中对移位后的图像与滤波器进行逐点乘法。
这个过程将两个图像元素的对应像素相乘。例如,当应用低通滤波器时,我们将对移位的傅里叶变换图像与低通滤波器逐点相乘。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
乘法滤波器是一种以像素值为权重的滤波器,它通过将滤波器的权重与图像的像素值相乘,来获得滤波后的像素值。具体地,假设乘法滤波器的权重为h(i,j),图像的像素值为f(m,n),那么滤波后的像素值g(x,y)可以表示为:
g(x,y) = ∑∑ f(m,n)h(x-m,y-n)
其中,∑∑表示对所有的(m,n)进行求和。
平移后的图像是指将图像进行平移操作后的结果。平移操作通常是指将图像的像素沿着x轴和y轴方向进行平移。平移后的图像与原始图像具有相同的大小和分辨率,但它们的像素位置发生了变化。在滤波操作中,平移后的图像可以用于与滤波器进行卷积运算,以实现滤波操作。
此操作抑制高频并保留低频,对于高通滤波器反之亦然。这个乘法过程对于去除不需要的频率和增强所需的频率是必不可少的,从而产生更清晰和更清晰的图像。
它使我们能够获得期望的频率响应,并在频域获得最终滤波图像。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(fftshifted_image * idealFilterLP(50,img.shape))), cmap='gray')
ax.set_title('Filtered Image in Frequency Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image in freq domain.png', bbox_inches='tight')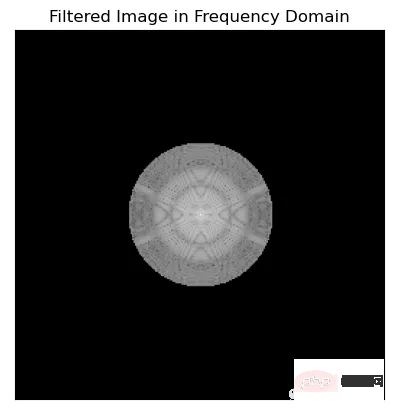
在可视化傅里叶频谱时,使用np.log(1+np.abs(x))和20*np.log(np.abs(x))之间的选择是个人喜好的问题,可以取决于具体的应用程序。
一般情况下会使用Np.log (1+np.abs(x)),因为它通过压缩数据的动态范围来帮助更清晰地可视化频谱。这是通过取数据绝对值的对数来实现的,并加上1以避免取零的对数。
而20*np.log(np.abs(x))将数据按20倍缩放,并对数据的绝对值取对数,这可以更容易地看到不同频率之间较小的幅度差异。但是它不会像np.log(1+np.abs(x))那样压缩数据的动态范围。
这两种方法都有各自的优点和缺点,最终取决于具体的应用程序和个人偏好。
在频域滤波后,我们需要将图像移回原始位置,然后应用逆FFT。为了实现这一点,需要使用逆FFT移位,它反转了前面执行的移位过程。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape)))), cmap='gray')
ax.set_title('Filtered Image inverse fft shifted')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('filtered image inverse fft shifted.png', bbox_inches='tight')
快速傅里叶逆变换(IFFT)是图像频率变换的最后一步。它用于将图像从频域传输回空间域。这一步的结果是在空间域中与原始图像相比,图像减少了噪声并提高了清晰度。
fig, ax = plt.subplots()
im = ax.imshow(np.log(1+np.abs(np.fft.ifft2(np.fft.ifftshift(fftshifted_image * idealFilterLP(50,img.shape))))), cmap='gray')
ax.set_title('Final Filtered Image In Spatial Domain')
ax.set_xticks([])
ax.set_yticks([])
fig.savefig('final filtered image.png', bbox_inches='tight')
我们再把所有的操作串在一起显示,
函数绘制所有图像
def Freq_Trans(image, filter_used): img_in_freq_domain = np.fft.fft2(image) # Shift the zero-frequency component to the center of the frequency spectrum centered = np.fft.fftshift(img_in_freq_domain) # Multiply the filter with the centered spectrum filtered_image_in_freq_domain = centered * filter_used # Shift the zero-frequency component back to the top-left corner of the frequency spectrum inverse_fftshift_on_filtered_image = np.fft.ifftshift(filtered_image_in_freq_domain) # Apply the inverse Fourier transform to obtain the final filtered image final_filtered_image = np.fft.ifft2(inverse_fftshift_on_filtered_image) return img_in_freq_domain,centered,filter_used,filtered_image_in_freq_domain,inverse_fftshift_on_filtered_image,final_filtered_image
使用高通、低通理想滤波器和高斯滤波器的直径分别为50、100和150像素,展示它们对增强图像清晰度的影响。
fig, axs = plt.subplots(12, 7, figsize=(30, 60))
filters = [(f, d) for f in [idealFilterLP, idealFilterHP, gaussianLP, gaussianHP] for d in [50, 100, 150]]
for row, (filter_name, filter_diameter) in enumerate(filters):
# Plot each filter output on a separate subplot
result = Freq_Trans(img, filter_name(filter_diameter, img.shape))
for col, title, img_array in zip(range(7),
["Original Image", "Spectrum", "Centered Spectrum", f"{filter_name.__name__} of Diameter {filter_diameter} px",
f"Centered Spectrum multiplied by {filter_name.__name__}", "Decentralize", "Processed Image"],
[img, np.log(1+np.abs(result[0])), np.log(1+np.abs(result[1])), np.abs(result[2]), np.log(1+np.abs(result[3])),
np.log(1+np.abs(result[4])), np.abs(result[5])]):
axs[row, col].imshow(img_array, cmap='gray')
axs[row, col].set_title(title)
plt.tight_layout()
plt.savefig('all_processess.png', bbox_inches='tight')
plt.show()
Sie können sehen, dass die Auswirkungen auf die Bildschärfe unterschiedlich sind, wenn Sie den Durchmesser der kreisförmigen Maske ändern. Mit zunehmendem Durchmesser werden mehr Frequenzen unterdrückt, was zu gleichmäßigeren Bildern mit weniger Details führt. Durch die Reduzierung des Durchmessers können mehr Frequenzen durchgelassen werden, was zu schärferen Bildern und mehr Details führt. Um den gewünschten Effekt zu erzielen, ist es wichtig, den richtigen Durchmesser zu wählen, da die Verwendung eines zu kleinen Durchmessers dazu führt, dass der Filter nicht effektiv genug ist, während die Verwendung eines zu großen Durchmessers zu viele Details zur Folge hat verloren gehen.
Im Allgemeinen wird der Gaußsche Filter aufgrund seiner Glätte und Robustheit häufiger bei Bildverarbeitungsaufgaben verwendet. In einigen Anwendungen, in denen eine schärfere Grenzfrequenz erforderlich ist, ist ein idealer Filter möglicherweise besser geeignet.
Die Verwendung von FFT zur Änderung der Bildfrequenz ist eine wirksame Methode zur Reduzierung von Rauschen und zur Verbesserung der Bildschärfe. Dazu gehört die Verwendung einer FFT zur Konvertierung des Bildes in den Frequenzbereich, die Verwendung geeigneter Techniken zur Filterung des Rauschens und die Verwendung einer inversen FFT zur Konvertierung des modifizierten Bildes zurück in den räumlichen Bereich. Durch das Verständnis und die Implementierung dieser Techniken können wir die Bildqualität für eine Vielzahl von Anwendungen verbessern.
Das obige ist der detaillierte Inhalt vonPython-Bildverarbeitung: Frequenzbereichsfilterung, Rauschunterdrückung und Bildverbesserung. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!




